КР №1 В-1

 

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра программного обеспечения информационных технологий

 

 

Факультет НиДО

Специальность ПОИТ

 

 

Контрольная работа № 1

по дисциплине «Основы алгоритмизации и программирования»

часть 1

Вариант № 5

 

 

Выполнил студент:

группа

Зачетная книжка №

  

  

 

 

Минск 2011

1). Задание

Найти 10 пар простых чисел, которые отличались бы друг от друга на 2 (3, 5; 11, 13 и т.д.). (Целое число Х является простым, если оно делится нацело только на единицу и само на себя).

Для проверки простоты числа, воспользуемся методом перебора делителей (т.к. по заданию найти необходимо всего 10 пар простых чисел).

Обычно перебор делителей заключается в переборе всех целых (как вариант: простых) чисел от 2 до квадратного корня из факторизуемого числа n и в вычислении остатка от деления n на каждое из этих чисел. Если остаток от деления на некоторое число p равен нулю, то p является делителем n. В этом случае либо n объявляется составным, и алгоритм заканчивает работу (если тестируется простота n), либо n сокращается на p и процедура повторяется (если осуществляется факторизация n). По достижении квадратного корня из n и невозможности сократить n ни на одно из меньших чисел, n объявляется простым.

n – проверяемое на простоту число (а так же число, с которого начинается поиск);

p – делитель;

f – счетчик пары;

S- счетчик количества пар простых чисел;

ОПИСАНИЕ АЛГОРИТМА

Вводим значение n.

Делителю p присваивается значение 2.

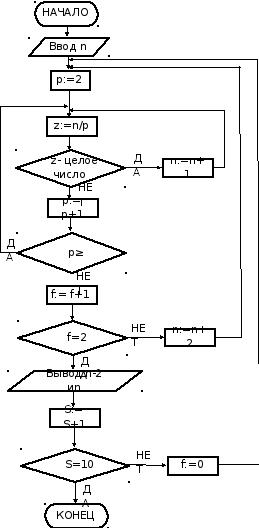
Вычисляется значение .

Проверяется значение z (целое или дробное). Если целое, то n – сложносоставное число. В этом случае его значение увеличивается на 1, вычисляется zи проводится проверка на целостность. Если z – дробное, то значение делителя р увеличивается на 1, вычисляется zи проводится проверка на целостность.

Выход из цикла происходит при достижении делителя pзначения ≥.

Значение переменной f увеличивается на 1.

Проверяется значение переменной f. Если f=1, значение nувеличивается на 2 и начинается поиск второго простого числа, отличного от исходного на 2. Если f=2, то пара простых чисел найдена и результат выводится на экран.

Увеличивается значение переменной Sна 1.

Проверяется значение S. Если S<10, то продолжается поиск пар простых чисел. При этом происходит обнуление счетчика пар.

2). Схема алгоритма.

На рис. 1, 2, 3 приведены три способа графического представления алгоритма.

Р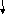 ис. 1. Схема алгоритма по ГОСТ 19. 701-90

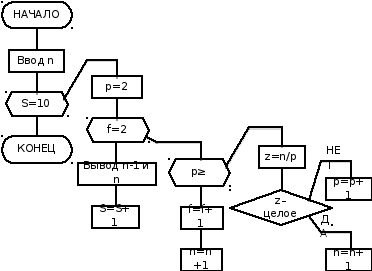
Рис. 2. Схема алгоритма, представленная методом Дамке

Ввод n
S=10
	p=2
		z z-целое =n/p
			да	нет
			p=p+1	n=n+1
		f=f+1
		n=n+2
	f=2
	Вывод ‘n-2’ и ‘n’
	S=S+1
	f=0

Рис. 3.ДиаграммаНасси-Шнайдермана