1. Определите амплитуду, период, циклическую частоту и начальную фазу колебаний, заданных уравнением: .
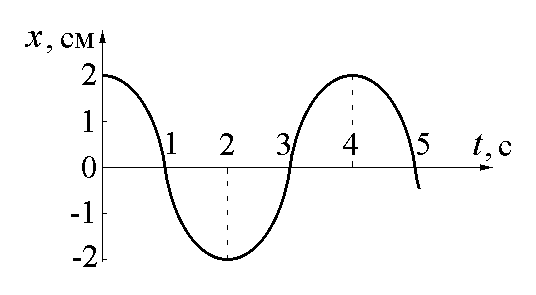
2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
3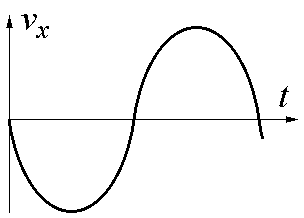
.
Линейный гармонический осциллятор
совершает колебания. График временной
зависимости проекции его скорости vx
представлен
на рисунке. Нарисуйте график, правильно
отражающий зависимость проекции
ускорения ax
от времени.
4. Частота колебаний ножки камертона 500 Гц, амплитуда колебаний 0,1 мм. Определите максимальное ускорение.
5.
Уравнение колебания тела массой 2 кг
имеет вид:
.
Определите кинетическую, энергию в
момент времени t = 6 с.
6. Диск радиусом 24 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно к. плоскости диска. Определите частоту колебаний такого физического маятника.
7.
Складываются
два гармонических колебания одного
направления с одинаковыми периодами и
равными амплитудами
.
Чему равна амплитуда результирующего
колебания при разности фаз
.
8. Точка совершает одновременно два гармонических колебания, происходящих во взаимно перпендикулярных направлениях и выражаемых уравнениями х = sin t/2 см и у = соs t см (время в секундах). Определите уравнение траектории точки, постройте ее с соблюдением масштаба и укажите направление движения.
9. Период затухающих колебаний 4 с, логарифмический декремент затухания 1,6, начальная фаза равна нулю. Смещение точки при t = Т/4 равно 4,5 см. Напишите уравнение движения этого колебания и постройте его график в пределах двух периодов.
10. Поперечная волна распространяется вдоль оси Х. Уравнение незатухающих колебаний источника дано в виде: у = 5sin 10t, см. Напишите уравнение, колебаний для точки, отстоящей на расстоянии 600 м от источника колебаний, если скорость волны 300 м/с.
11. Найдите разность фаз колебаний двух точек, отстоящих на расстоянии 2 м друг от друга, если длина волны равна 1 м.
Модуль 3. Колебания и волны
Вариант № 7
1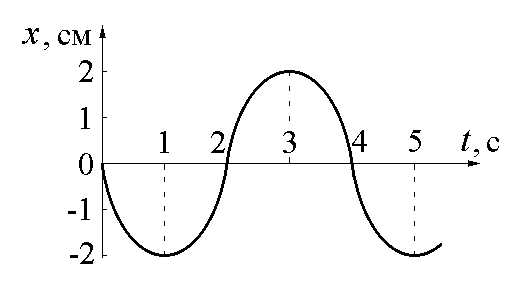
.
Уравнение гармонических колебаний
имеет вид:
.
Определите амплитуду, циклическую
частоту, период и начальную фазу этих
колебаний.
2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
3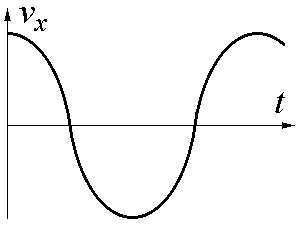
.
Линейный гармонический осциллятор
совершает колебания. График временной
зависимости проекции его скорости vx
представлен
на рисунке. Нарисуйте график, правильно
отражающий зависимость проекции
ускорения ax
от времени.
4.
Материальная точка совершает
гармонические колебания, уравнение
которых имеет вид:
,
мм. Каково значение ускорения точки в
момент
времени t
= 3 с?
5.
Материальная точка массой 20 г колеблется
согласно уравнению:
.
Найдите частоту колебаний, максимальную
силу, действующую на точку и ее полную
энергию.
6. Один маятник совершает в минуту 40, а другой - 60 качаний. Как относятся длины этих маятников?
7. Точка участвует в двух одинаково направленных колебаниях одного периода с одинаковыми начальными фазами, амплитуды колебаний А1 = 3 см и А2 = 4 см. Найдите амплитуду результирующего колебания.
8. Материальная точка одновременно участвует в двух взаимно перпендикулярных колебаниях одинаковой частоты, заданных уравнениями: х = 3sin 0t, и у = 3sin(0t + /2 ), см. Найдите уравнение траектории, постройте ее с соблюдением масштаба и укажите направление движения.
9. За 600 секунд амплитуда затухающих колебаний маятника уменьшилась в 3 раза. Определите коэффициент затухания.
10. 0т источника колебаний распространяются волны вдоль прямой линии. Амплитуда колебаний 10 см. Каково смещение точки, удаленной от источника на 3/4 длины волны в момент, когда от начала колебаний источника прошло время, равное 0,9 периода колебаний?
11. Волны распространяются в упругой среде со скоростью 75 м/с. Наименьшее расстояние между точками среды, фазы колебаний которых противоположны, равно 2 м. Определите период колебаний.
Модуль 3. Колебания и волны
Вариант N 8
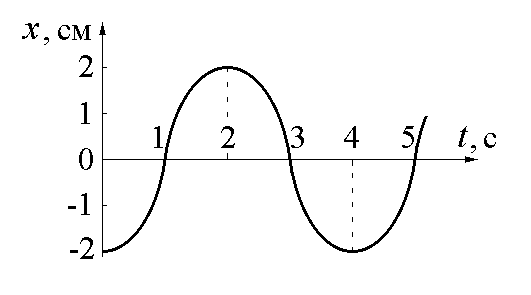1.
Уравнение гармонических. колебаний
тела имеет вид:
.
Определите амплитуду, циклическую
частоту, период и начальную фазу.