
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •1. Определите амплитуду, период, циклическую частоту и начальную фазу колебаний, заданных уравнением: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •1. Определите амплитуду, период, циклическую частоту и начальную фазу колебаний, заданных уравнением: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •1. Определите амплитуду, период, циклическую частоту и начальную фазу колебаний, заданных уравнением: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде:
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •4. Уравнение движения точки дано в виде . Найдите моменты времени, в которые достигается максимальная скорость и максимальное ускорение.
- •1. Определите амплитуду, период, циклическую частоту и начальную фазу колебаний, заданных уравнением: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •1 . Определите амплитуду, период, циклическую частоту и начальную фазу колебаний, заданных уравнением: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •1. Определите амплитуду, период, циклическую частоту и начальную фазу колебаний, заданных уравнением: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •2 . Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •1. Определите амплитуду, период, циклическую частоту и начальную фазу колебаний, заданных уравнением: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
- •11. Две точки находятся на прямой, вдоль которой распространяются волны со скоростью 40 м/с. Частота колебаний 20 Гц, расстояние между точками 40 см. Найдите разность фаз колебаний этих точек.
2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
3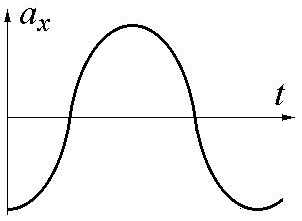 .
Линейный гармонический осциллятор
совершает колебания. График временной
зависимости проекции его ускорения аx
представлен
на рисунке. Нарисуйте график, правильно
отражающий зависимость проекции скорости
vx
от времени.
.
Линейный гармонический осциллятор
совершает колебания. График временной
зависимости проекции его ускорения аx
представлен
на рисунке. Нарисуйте график, правильно
отражающий зависимость проекции скорости
vx
от времени.
4. Точка колеблется с амплитудой 10 см и периодом 20 с. Начальная фаза равна нулю. Напишите уравнение колебаний. Найдите смещение от положения равновесия, скорость и ускорение точки в момент времени t = 2 с.
5.
Материальная точка массой 5 г колеблется
по уравнению:
![]() .Напишите
уравнение для силы, действующей на
точку, и уравнение кинетической энергии.
.Напишите
уравнение для силы, действующей на
точку, и уравнение кинетической энергии.
6. Однородный стержень длиной 1 м совершает малые колебания в вертикальной плоскости около горизонтальной оси, проходящей на расстоянии 10 см от его верхнего конца. Определите период колебаний стержня.
7. Точка участвует в двух одинаково направленных колебаниях: х1 = А1sin t и х2 = А2соs t, где А1 = 1 см, А2 = 2 см, = 1 рад/с. Определите амплитуду результирующих колебаний и их частоту.
8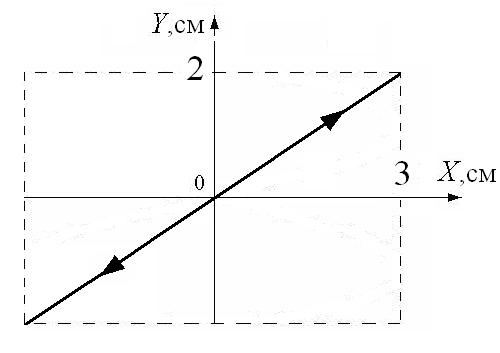 .
Точка одновременно участвует в двух
взаимно перпендикулярных гармонических
колебаниях с циклическими частотами
ωX
= 2π рад/с и ωY
.
Траектория точки представлена на
рисунке. Определите амплитуды, начальные
фазы, частоты и Напишите законы изменения
координат
и
.
.
Точка одновременно участвует в двух
взаимно перпендикулярных гармонических
колебаниях с циклическими частотами
ωX
= 2π рад/с и ωY
.
Траектория точки представлена на
рисунке. Определите амплитуды, начальные
фазы, частоты и Напишите законы изменения
координат
и
.
9.
Задано уравнение колебаний:
![]() ,
см. Чему равна амплитуда и координата
в момент времени 1 с.
,
см. Чему равна амплитуда и координата
в момент времени 1 с.
10. Поперечная волна распространяется вдоль оси Х. Уравнение незатухающих колебаний источника дано в виде: у = 10sin t, см. Напишите уравнение координаты у для точек волны в момент t = 2 с после начала колебаний, если скорость волны 2 м/с.
11. Две точки находятся на одной прямой, вдоль которой распространяются волны со скоростью 50 м/с. Период колебаний 0,05 с. Расстояние между точками х = 50 см. Найдите разность фаз колебаний.
Модуль 3. Колебания и волны
Вариант N 25
1
.
Уравнение гармонических колебаний тела
имеет вид:
![]() .
Определите амплитуду, циклическую
частоту, период и начальную фазу этих
колебаний.
.
Определите амплитуду, циклическую
частоту, период и начальную фазу этих
колебаний.
2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .
3. Линейный гармонический осциллятор совершает колебания. График временной зависимости его координаты х представлен на рисунке. Нарисуйте график, правильно отражающий зависимость проекции скорости vx от времени.
4.
Уравнение гармонического колебания
тела имеет вид:
![]() .Определите
максимальное ускорение и скорость в
момент времени t
= 1 с.
.Определите
максимальное ускорение и скорость в
момент времени t
= 1 с.
5.
Уравнение гармонического колебания
тела массой 2 кг имеет вид:
![]() .
Определите кинетическую и потенциальную
энергию в момент времени t
= 4 с.
.
Определите кинетическую и потенциальную
энергию в момент времени t
= 4 с.
6. Однородный стержень длиной 1 м совершает малые колебания в вертикальной плоскости около горизонтальной оси, проходящей на расстоянии 10 см от его верхнего конца. Определите частоту колебаний.
7. Складываются два гармонических колебания одного направления с одинаковыми периодами Т = 1 с и амплитудами А1 = 2 см, А2 = 3 см. Начальные фазы колебаний 1 = /2 и 2 = /4. Определите амплитуду и начальную фазу результирующего колебания. Напишите его уравнение.
8. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, заданных уравнениями: х = cos t и у = cos(t/2). Найдите уравнение траектории и вычертить ее с соблюдением масштаба.
9. Амплитуда 3-го колебания больше амплитуды 7-го колебания в 8 раз. Чему равен логарифмический декремент затухания?
10.Поперечная волна распространяется вдоль оси Х. Уравнение незатухающих колебаний источника дано в виде: у = 10sin 300t, см. Найдите смещение от положения равновесия точки, находящейся на расстоянии 50 см от источника колебаний через 0,01 с после начала колебаний. Скорость распространения колебаний 150 м/с.
