Модуль 3. Колебания и волны

Вариант N 1

1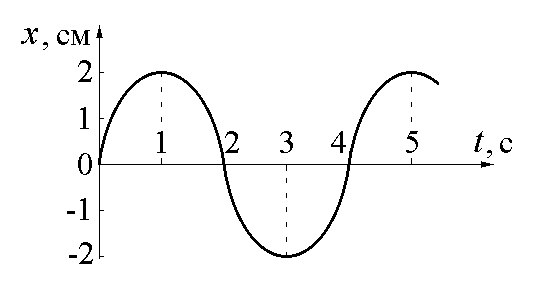 . Уравнение гармонических колебаний имеет вид: . Чему равны период, амплитуда и начальная фаза этих колебаний?

2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в СИ уравнение гармонических колебаний в виде: .

3. Линейный гармонический осциллятор совершает колебания. График временной зависимости его координаты х представлен на рисунке. Нарисуйте график, правильно отражающий зависимость проекции скорости v_x от времени.

4. Уравнение движения точки дано в виде . Найдите моменты времени, в которые достигается максимальная скорость и максимальное ускорение.

5. К пружине подвешен груз. Зная, что максимальная кинетическая энергия колебаний груза равна 1 Дж, найдите коэффициент упругости пружины. Амплитуда колебаний 5 см.

6. Из однородного диска радиусом R сделали физический маятник. Вначале ось проходит через образующую диска, потом - на расстоянии R/2 от центра диска. Определите отношение периодов колебаний дисков.

7. Постройте векторную диаграмму сложения амплитуд и напишите уравнение результирующего гармонического колебания, полученного от сложения одинаково направленных колебаний, заданных уравнениями: х₁ = 4sint, см и x₂ = 3sin(t + /2).

8. Материальная точка одновременно участвует в двух взаимно перпендикулярных колебаниях одинаковой частоты, заданных уравнениями: х = 2sin(₀t+ /2), см и у = 2sin₀t, см. Найдите уравнение траектории, постройте ее с соблюдением масштаба и укажите направление движения.

9. Амплитуда колебаний маятника, длиной 1 м за 10 минут уменьшилась в 2 раза. Определите логарифмический декремент затухания.

10. Поперечная волна распространяется вдоль оси Х. Уравнение незатухающих колебаний источника дано в виде: у = 10sin 0,5t, см. Напишите уравнение колебаний для точек волны в момент t = 4 c после начала колебаний.

11. Две точки находятся на прямой, вдоль которой распространяются волны со скоростью 40 м/с. Частота колебаний 20 Гц, расстояние между точками 40 см. Найдите разность фаз колебаний этих точек.

Модуль 3. Колебания и волны

Вариант N 2

1 . Определите амплитуду, период, циклическую частоту и начальную фазу колебаний, заданных уравнением: .

2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .

3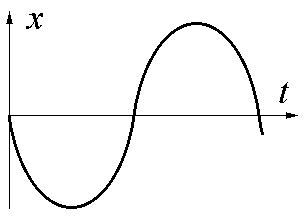 . Линейный гармонический осциллятор совершает колебания. График временной зависимости его координаты х представлен на рисунке. Нарисуйте график, правильно отражающий зависимость проекции скорости v_x от времени.

4. Напишите уравнение гармонического колебательного движения, если максимальное ускорение точки 49,3 см/с², период колебаний 2 с и смещение точки от положения равновесия в начальный момент времени 25 мм.

5. Материальная точка массой 20 г колеблется по уравнению: . Найдите период колебаний, максимальную силу, действующую на точку и ее полную энергию.

6. Обруч диаметром 56,5 см висит на гвозде, вбитом в стену, и совершает малые колебания в плоскости, параллельной стене. Найдите период этих колебаний.

7. Точка участвует в двух одинаково направленных колебаниях: х₁ = А₁sin t и х₂ = А₂соs t, где А₁ = 1 см, А₂ = 2 см,  = 1 рад/с. Определите амплитуду результирующих колебаний и их частоту.

8. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях: х = 2sin t и у = 2cos t. Найдите уравнение траектории, постройте ее с соблюдением масштаба и укажите направление движения.

9. Амплитуда затухающих колебаний маятника за 2 минуты уменьшилась вдвое. Во сколько раз она уменьшится за 5 минут?

10. Поперечная волна распространяется вдоль оси Х. Уравнение незатухающих колебаний источника дано в виде: у = 10sin 0,5t, см. Напишите уравнение, колебаний для точки, отстоящей на расстоянии 600 м от источника колебаний, если скорость волны 300 м/с.

11. Определите скорость распространения волн в упругой среде, если разность фаз колебаний двух точек среды, отстоящих друг от друга на 10 см, равна /3, а частота колебаний 25 Гц.

Модуль 3. Колебания и волны

Вариант N 3

1 . Уравнение гармонических колебаний тела имеет вид: . Чему равны амплитуда, частота и начальная фаза колебаний?

2. Зависимость координаты колеблющегося тела от времени представлена графиком на рисунке. Напишите в си уравнение гармонических колебаний в виде: .

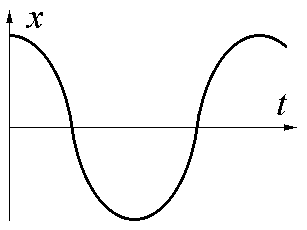
3. Линейный гармонический осциллятор совершает колебания. График временной зависимости его координаты х представлен на рисунке. Постройте график, правильно отражающий зависимость проекции скорости v_x от времени.

4. Амплитуда гармонических колебаний 5 см, период 4 с. Найдите максимальную скорость колеблющейся точки и максимальное ускорение.

5. Амплитуда гармонических колебаний материальной точки А = 0,3 см, полная энергия колебаний W = 310^-7 Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила F = 10^-5 Н?

6. Как относятся частоты колебаний математических маятников, если длины относятся как 1:4?

7. Найдите амплитуду и начальную фазу гармонического колебания, полученного от сложения одинаково направленных колебаний, заданных уравнениями: х₁ = 3sint, см и x₂ = 4sin(t + /2), см. Напишите уравнение результирующего колебания и постройте векторную диаграмму сложения амплитуд.

8. Точка совершает одновременно два гармонических колебания, происходящих во взаимно перпендикулярных направлениях и выражаемых уравнениями х = sin t/2 и у = cos t (длина - в см, время в секундах). Определите уравнение траектории точки, постройте ее с соблюдением масштаба и укажите направление движения.

9. За 8 минут амплитуда затухающих колебаний маятника уменьшилась в 3 раза. Определите коэффициент затухания.

10. Поперечная волна распространяется вдоль оси Х. Уравнение незатухающих колебаний источника дано в виде: у = 10sin 0,5t, см. Напишите уравнение волны, если скорость распространения колебаний 300 м/с.

11. Волны распространяются в упругой среде со скоростью 75 м/с. Наименьшее расстояние между точками среда, фазы колебаний которых противоположны, равно 2 м. Определите период колебаний.

Модуль 3. Колебания и волны

Вариант N 4