11. Обернені тригонометричні функції
Арксинусом числа а називається таке число х з
інтервалу
,
синус якого дорівнює а.
Арккосинусом числа а називається таке число х з інтервалу [0; ], косинус якого дорівнює а.
Арктангенсом числа а називається таке число х з інтервалу
,
тангенс якого дорівнює а.
Арккотангенсом
числа а
називається таке число х
з
інтервалу (0; ), котангенс якого дорівнює а.
З визначення обернених тригонометричних функцій випливає:
Для від’ємних значень аргументу:
12. Тригонометричні рівняння
При а = 1; 0; –1 розв’язок рівняння записується у вигляді (n Z):
Слід пам’ятати:
При |а| > 1 рівняння sin x = a і cos x = a коренів не мають!
13. Приклади для обчислення
Спростити вираз:
1)
2)
3)
4)
5)
6)
7)
8)
9)
Обчислити:
.Відомо, що
.
Знайти:
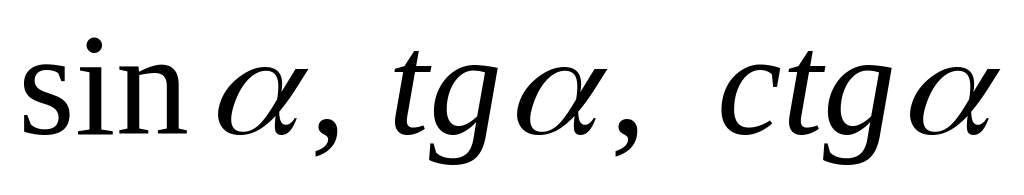.Відомо, що
.
Знайти:
.*Знайдіть
,
якщо
*Відомо, що
.
Знайдіть всі можливі значення виразу:
.**Обчислити
,
якщо
.**Відомо, що
.
Знайти:
.
9.
**Відомо, що
. Знайдіть
10.
. **Знайдіть найбільше та найменше
значення виразу
11.* Виразити дані тригонометричні функції через функції аргументу, що вдвічі менші від даного.
13.
*Дано:
Знайти:
14. **Довести, що
15. Спростити.
1)
2)
3) *
4) *
5) **
6) **
7) **
8) **
9) ***
10) ***
16.*** Довести тотожність:
1)
2)
3)
17. Знайти значення виразу:
1)
2)
3)
4)
18. Обчисліть значення:
1)
2)
3)
4)
18. Розв’яжіть найпростіші тригонометричні рівняння
1) sin
x
=
2
cos
2x
=1
sin
= 0
2) cos
x = -
3)
ctg
3x = 4
4)
5) sin
3x = 1 2 cos (4x) =
6)
sin 2x +1 =0
19.* Розв’яжіть рівняння, що зводяться до квадратних:
1)
2)
3)
4)
5)
6)
20** Розв’яжіть рівняння, права частина яких дорівнює нулю, а ліва розкладається на множники:
1)
2)
3)
4)
5)
21.*** Розв’яжіть однорідні тригонометричні рівняння.
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
