- •Министерство образования Республики Беларусь
- •1. Обзор существующих методов расчёта характеристик сигналов на выходе линейных устройств
- •1.1. Общие сведения о методах расчета
- •1.2. Классический метод
- •1.3. Спектральный метод
- •1.4. Операторный метод
- •1.5. Временной метод, или метод интеграла Дюамеля
- •2. Содержание спектрального метода анализа линейных устройств
- •2.1. Общие сведения
- •2.2. Основная формула
- •2.3. Вычисление импульсных характеристик
- •2.4. Вычисление сигнала на выходе системы
- •2.5. Геометрическая интерпретация процесса
- •4. Расчёт амплитудно-частотной и фазо-частотной характеристик устройства.
- •5. Расчёт спектральной плотности и формы выходного сигнала.
- •6. Программа расчёта на эвм
2.4. Вычисление сигнала на выходе системы
Как
пример использования спектрального
метода решим задачу о прохождении
экспоненциального видеоимпульса
напряжения
![]() черезRC-цепь,
рассмотренную выше. В данном случае
спектральная плотность входного сигнала
черезRC-цепь,
рассмотренную выше. В данном случае
спектральная плотность входного сигнала
![]() и задача сводится к вычислению интеграла,
входящего в выражение:
и задача сводится к вычислению интеграла,
входящего в выражение:
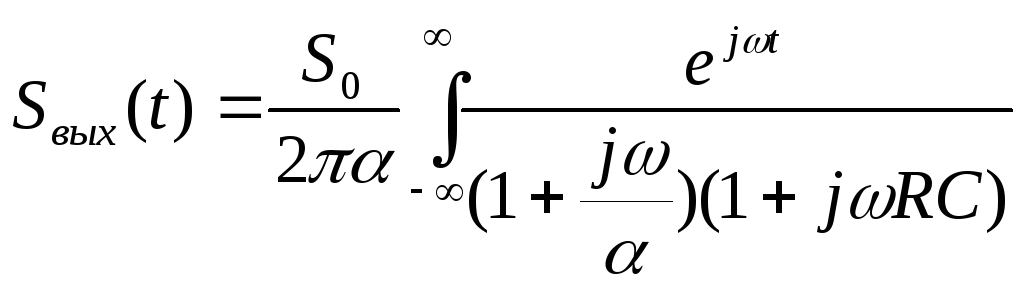 .
.
Раскладывая алгебраическую часть подынтегральной функции
на элементарные дроби, имеем:
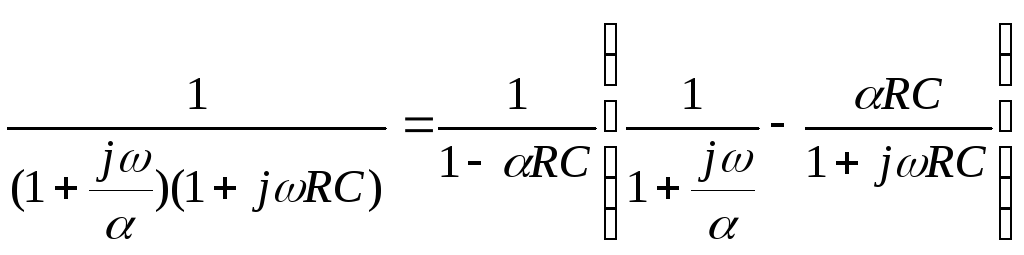 .
.
Структура слагаемых, стоящих в правой части выражения в скобках, позволяет непосредственно использовать результат, полученный при вычислении импульсной характеристики RC-цепи, и записать решение при t>0:
![]() (6)
(6)
Естественно, что при t<0
![]() (7)
(7)
![]() (10)
(10)
2.5. Геометрическая интерпретация процесса
Спектральный
метод позволяет наглядно интерпретировать
преобразования сигналов, которые
происходят при их прохождении через
линейные стационарные системы. Системный
оператор T
– это правило перехода от вектора
![]() некоторого линейного пространства к
новому вектору
некоторого линейного пространства к
новому вектору![]() .
В самом общем случае можно считать, что
операторT
изменяет форму вектора
.
В самом общем случае можно считать, что
операторT
изменяет форму вектора
![]() в
в![]() .
Норма
.
Норма![]() не будет равна
не будет равна
норме
![]() :
:
![]()
![]()
Кроме
того, между векторами ![]() и
и
![]() возникает
некоторый угол
возникает
некоторый угол![]() .
.
По формуле Рэлея, энергия выходного сигнала
![]() ,
(16)
,
(16)
где
![]() --
энергетический спектр сигнала на входе.
--
энергетический спектр сигнала на входе.
В
соответствии с формулой (16), выходной
энергетический спектр ![]() .
.
![]() (17)
(17)
Величину (17) называют частотным коэффициентом передачи по мощности системы на заданной частоте ω. Поскольку этот коэффициент вещественный, вычисление энергии выходного сигнала оказывается гораздо более простой задачей по сравнению с поиском самой формы выходного сигнала.
Теперь, рассмотрев различные методы анализа линейных цепей и сделав вывод о том, что наибольшую практическую пользу имеет спектральный метод анализа из-за своей простоты и наглядности, приступим к непосредственному расчёту сигнала на выходе линейного устройства. Расчёты приведены в следующих пунктах.
3. Расчёт амплитудного и фазового спектров входного сигнала.
В задании приведён входной сигнал. Он имеет следующий вид:



 S(t)
S(t)
![]()
![]()
![]() t
t
рис.1
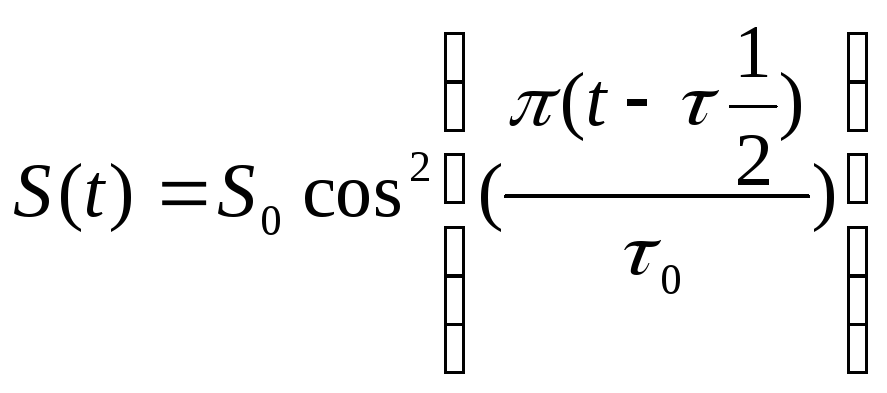
где
![]() с,
с,![]() c,
c,
![]() B
B
Далее для нахождения спектральной плотности сигнала S(t) нам необходимо найти прямое преобразование Фурье . В нашем случае необходимо посчитать интеграл:
![]() ,
,
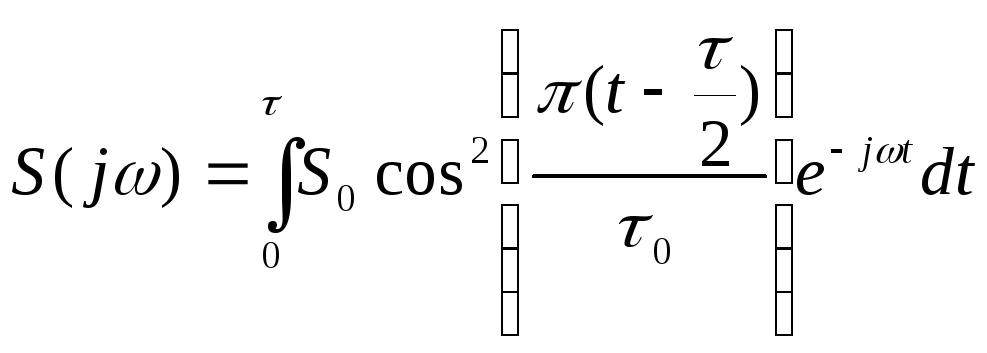 ,
,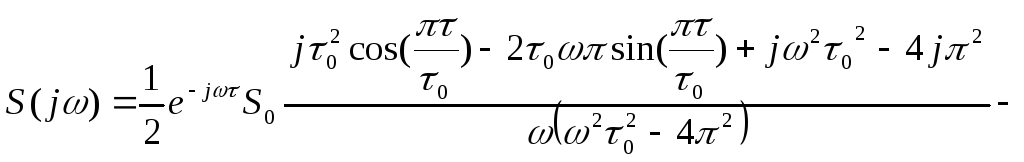
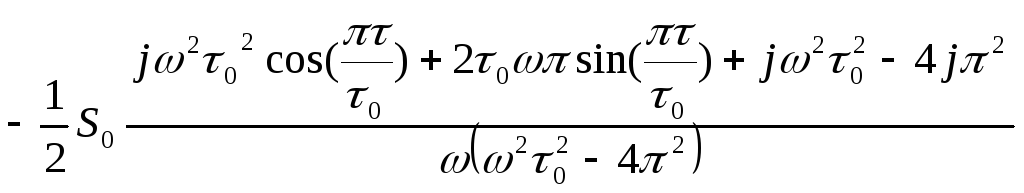 .
.
Это выражение необходимо путём преобразований привести к виду a+jb. В итоге получаем:
![]() ,
,
г![]() де
де
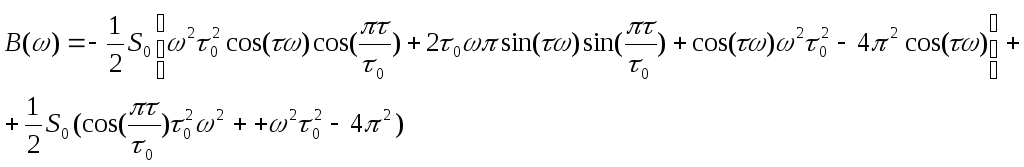
![]()
Таким
образом, действительная часть спектра
будет равна![]() ,а
мнимая часть --
,а
мнимая часть --![]() .
Знаменатель
.
Знаменатель![]() оставлен
для того, чтобы не усложнять конечные
формулы действительной и мнимой частей.
оставлен
для того, чтобы не усложнять конечные
формулы действительной и мнимой частей.
Для
построения амплитудного и фазового
спектров сигнала приводим наше выражение
к виду
![]() ,
где
,
где![]() и
и![]() --
модуль и аргумент спектра входного
сигнала соответственно. В нашем случае
--
модуль и аргумент спектра входного
сигнала соответственно. В нашем случае![]() ,
,![]() .
.
По этим данным строятся графики амплитудного и фазового спектров входного сигнала.
Амплитудный спектр входного сигнала
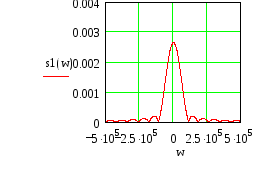
Фазовый спектр входного сигнала