3. Построение проекций точки по ее координатам

Если заданы координаты какой-либо точки А (x, y, z), тогда проекции точки строят следующим образом: сначала откладывают абсциссу по оси ОХ; затем проводят вертикальную линию; далее на ней откладывают ординату по оси OY и аппликату по оси OZ. По оси OY получают горизонтальную проекцию А₁, по оси OZ - фронтальную А₂. Профильную проекцию А₃ строят по А₁ и А₂ (либо по координатам). Например, построим проекции точек А (10, 20, 30).Построения показаны на рис. 1.4.

Необходимо помнить, что положение горизонтальной проекции определяется координатами х и y, фронтальной проекции -координатами х и z, профильной проекции – координатами y и z. Тогда ордината y всегда характеризует положение горизонтальной проекции, а аппликата – фронтальной.

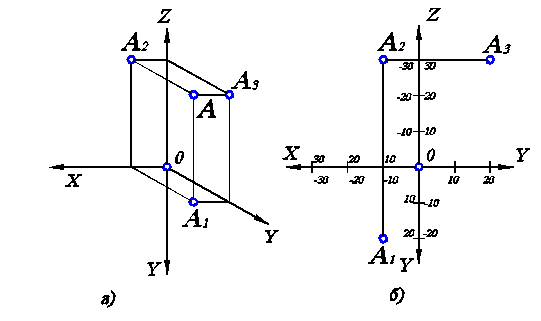
Рис.1.4. Взаимосвязь координат точки и ее проекций: а) вид в аксонометрии; б) комплексный чертеж.

Исходя из тех же положений, решается обратная задача – определение координат точки по ее проекциям. Если на комплексном чертеже изображены проекции точки, тогда, измерив соответствующие расстояния, определяем ее координаты (см. рис. 1.4, б). Причем для определения всех трех координат достаточно двух проекций, т.к. любая пара проекций определяет три координаты.

Вопросы для самоконтроля:

1. Какие виды проецирования существуют ?

2. В чем заключаются метод Г. Монжа ?

3. Понятие комплексного чертежа или эпюра ?

4. Какое положение точки по отношению к плоскостям проекций называют частным?

5. Каким образом определяют удаленность точек от плоскостей проекций?

Тестовые задания

1. Фронтальная плоскость проекций обозначается:

а) П₂;

б) П₃;

в) П₁.

2. Какие координаты будет иметь точка, принадлежащая горизонтальной плоскости проекций ?

а) (х; y; 0);

б) (0; у; z);

в) (х; 0; z).

3. Какие координаты будет иметь точка, лежащая на оси z ?

а) (0; у; z);

б) (0, 0, z);

в) (х; 0; 0).

4. Профильная проекция точки определяется координатами:

а) (х; у);

б) (у; z);

в) (х; z).

5. Какие координаты будет иметь точка, принадлежащая фронтальной плоскости проекций ?

а) (х; y; 0);

б) (0; у; z);

в) (х; 0; z).

Глава 2. Прямая

Следующим после точки геометрическим объектом, проецирование которого мы рассматриваем, является прямая линия. Поскольку ее положение в пространстве однозначно определяется двумя точками, то и для определения положения проекций прямой также достаточно зафиксировать проекции двух точек. Поэтому для построения проекций прямой можно использовать все правила, касающиеся проецирования точки.

2.1. Прямые частного и общего положения

Прямая называется прямой частного положения, если она занимает в пространстве частное положение, а именно либо параллельна, либо перпендикулярна одной из плоскостей проекций.

2.1.1. Прямые уровня

Прямой уровня называется прямая, параллельная одной из плоскостей проекций. Поскольку плоскостей проекций три, то и прямых уровня тоже три.

а). Прямая, параллельная горизонтальной плоскости проекций П₁, называется горизонтальной прямой уровня или горизонталью и обозначается h.

б). Прямая, параллельная фронтальной плоскости проекций П₂, называется фронтальной прямой уровня или фронталью и обозначается f.

в). Прямая, параллельная профильной плоскости проекций П₃, называется профильной линией уровня и обозначается p.

Исходя из положения прямых уровня в пространстве, их проекции выглядят как показано на рис. 2.1.

Горизонталь характерна тем, что ее фронтальная проекция параллельна оси ОХ. Фронталь характерна тем, что ее горизонтальная проекция параллельна оси ОХ. При этом по правилу взаимосвязи проекций расстояние от f₃ до оси OZ равно расстоянию от f₁ до оси ОХ. У профильной линии уровня и фронтальная и горизонтальная проекции перпендикулярны оси ОХ.

Очевидно, что если прямая параллельна какой-либо плоскости, то на эту плоскость она проецируется в натуральную величину (без искажений). Поэтому h₁, f₂, p₃ – это натуральная величина соответствующих прямых h, f, p.

 - угол наклона прямой уровня к П₁,

 - угол наклона прямой уровня к П₂,

 - угол наклона прямой уровня к П₃.

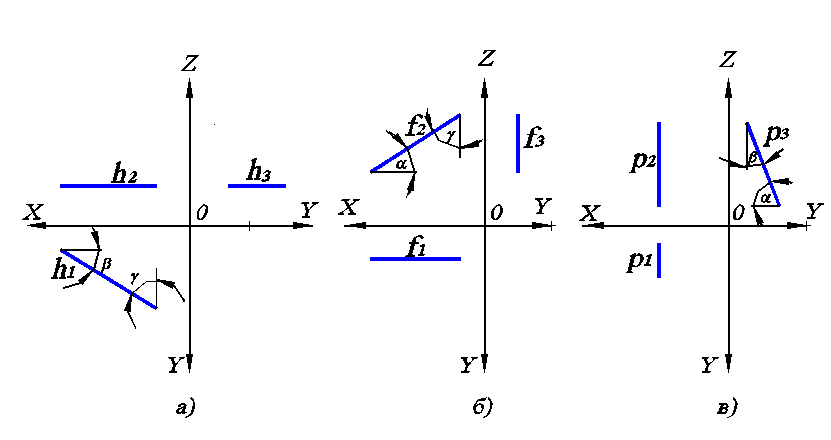
Рис. 2.1. Линии уровня на комплексном чертеже: а) горизонтальная линия уровня; б) фронтальная линия уровня; в) профильная линия уровня.