Глава 1. Метод проекций

Правила построения изображений, излагаемые в курсе начертательной геометрии, основаны на методе проекций. Рассмотрение метода проекций начинают с построения проекции точки, на примере которого рассматривают все базовые понятия и правила проецирования.

1. Центральное, параллельное и ортогональное проецирование

Наиболее общим методом проецирования является центральное проецирование (рис.1.1, а). Сущность центрального проецирования заключается в следующем: пусть даны плоскость П и точка S (SП). Возьмем произвольную точку А (АП, АS). Через заданную точку S и точку А проводим прямую SА и отмечаем точку А₀, в которой эта прямая пересекает плоскость П. Плоскость П называют плоскостью проекций , точку S центром проецирования, полученную точку А₀ – центральной проекцией точки А на плоскость П, прямую SА – проецирующей прямой. Аналогично можно получить проекцию любой другой точки.

Частным случаем центрального проецирования является параллельное (рис. 1.1, б), когда центр проецирования находится в бесконечности. Тогда проецирующие лучи параллельны друг другу.

Еще более частный случай, при котором проецирующие лучи перпендикулярны плоскости проекций (рис. 1.1, в), называется ортогональным проецированием.

В дальнейшем будем рассматривать лишь ортогональное проецирование, т.к. построение всех чертежей основано на этом методе.

Рис. 1.1. Методы проецирования: а) центральное; б) параллельное; в) ортогональное.

1.2. Свойства ортогонального проецирования

Решение любых задач начертательной геометрии и все дальнейшие построения основываются на следующих свойствах:

1. Проекция точки – есть точка.

2. Проекция прямой – есть прямая.

3. Проецирующий луч проецируется в точку.

4. Точка принадлежит прямой линии, если одноименные проекции точки принадлежат одноименным проекциям прямой линии.

5. Прямые в пространстве параллельны, если их одноименные проекции параллельны.

6. Прямой угол проецируется в прямой, если одна из его сторон параллельна плоскости проекций, а другая не перпендикулярна к ней.

7. Прямая линия параллельна плоскости, если она параллельна любой прямой, принадлежащей заданной плоскости.

8. Проекция плоской фигуры – есть плоская фигура.

Решение любых задач начертательной геометрии и все дальнейшие построения основываются именно на этих свойствах.

3. Эпюр Монжа или комплексный чертеж

Проекция геометрического объекта на одну плоскость не дает полного и однозначного представления о самом геометрическом объекте. Рассмотрим проецирование на три взаимно перпендикулярные плоскости (рис. 1.2), одна из которых расположена горизонтально, а две другие вертикально.

Тогда плоскость П₁ называется горизонтальной плоскостью проекций, П₂ - фронтальной плоскостью проекций (т.к. она расположена перед нами по фронту), П₃ - профильной плоскостью проекций (расположена в профиль по отношению к наблюдателю). Соответственно А₁ - горизонтальная проекция точки А, А₂ -фронтальная проекция точки А, А₃ - профильная проекция точки А. Оси ОХ, ОY, OZ называются осями проекций. Они аналогичны координатным осям декартовой системы координат с той лишь разницей, что ось ОХ имеет положительное направление не вправо, а влево.

Несмотря на наглядность, с чертежом, изображенным на рис 1.2, а работать неудобно, т.к. плоскости на нем показаны с искажениями. Удобнее выполнять различные построения на чертеже, где плоскости проекций расположены в одной плоскости, а именно, плоскости чертежа. Для этого надо горизонтальную плоскость проекций развернуть вокруг оси ОХ на 90 и совместить с фронтальной так, чтобы передняя пола горизонтальной плоскости ушла вниз, а задняя вверх. После чего профильную плоскость проекций развернуть до совмещения с фронтальной. Для этого ее нужно развернуть на 90 вокруг оси OZ, причем переднюю полу плоскости развернем вправо, а заднюю влево. Этот метод предложил Г. Монж. В результате полученное изображение называют трехкартинный комплексный чертеж (эпюр Монжа), рис. 1.2, б. Так как ось ОY разворачивается вместе с двумя плоскостями П₁ и П₃ , то на комплексном чертеже ее изображают дважды.

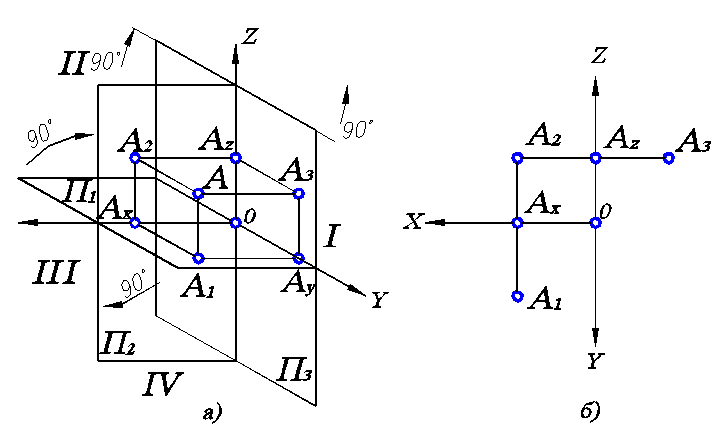
Рис. 1.2. Построение эпюра Монжа:

а) пространственная картина расположения проекций точки А; б) трехкартинный комплексный чертеж

Из этого следует важное правило взаимосвязи проекций. А именно, исходя из рис. 1.2, а очевидно А₁А_x = ОА_y = А_zА₃. Следовательно, это правило можно сформулировать так: расстояние от горизонтальной проекции точки до оси ОХ равно расстоянию от профильной проекции точки до оси ОZ. Тогда по двум любым проекциям точки можно построить третью. Горизонтальную и фронтальную проекции точки А связывает вертикальная линия связи, а фронтальную и профильную проекции – горизонтальная.

3. Проецирование точек, занимающих частное положение в пространстве

Частным положением точки считаем такое, при котором она находится либо на оси проекций, либо на плоскости проекций. Так, если точка расположена на оси проекций, тогда две ее проекции лежат на этой оси, а третья в начале координат. Если точка расположена на плоскости проекций, тогда одна из ее проекций лежит в этой же плоскости, а две другие – на осях проекций.

В качестве примера рассмотрим построение проекций точки Е, принадлежащей оси OY, и точки F, лежащей в профильной плоскости проекций (рис. 1.3).

Для точек, занимающих частное положение в пространстве, построения следует начинать с проекций, принадлежащих либо оси, либо плоскости проекций.

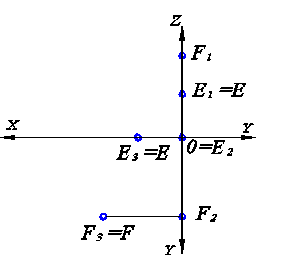
Рис. 1.3. Проекции точек, занимающих частное положение по отношению к плоскостям проекций.