Швидкість і прискорення точки при координатному способі опису

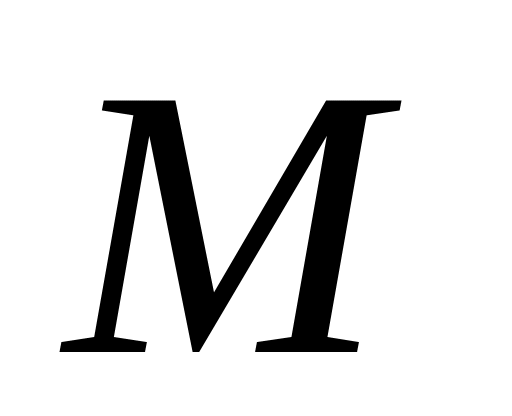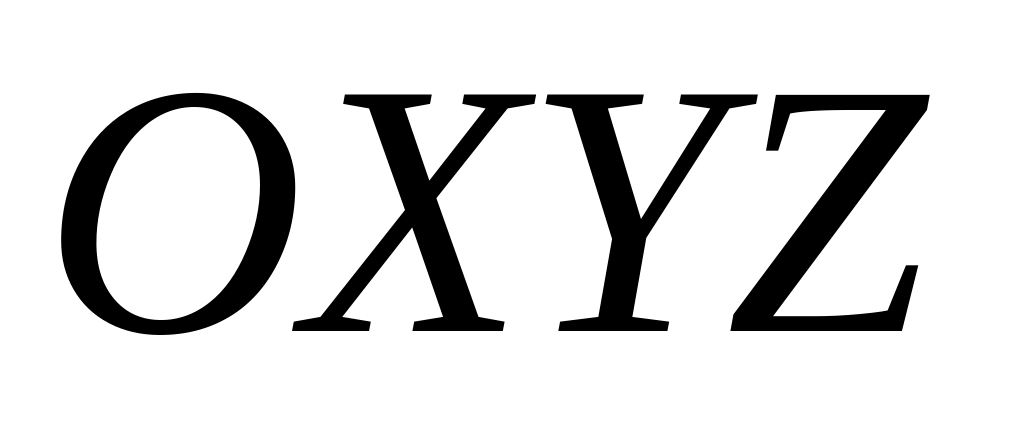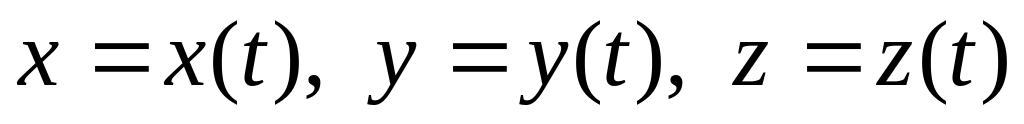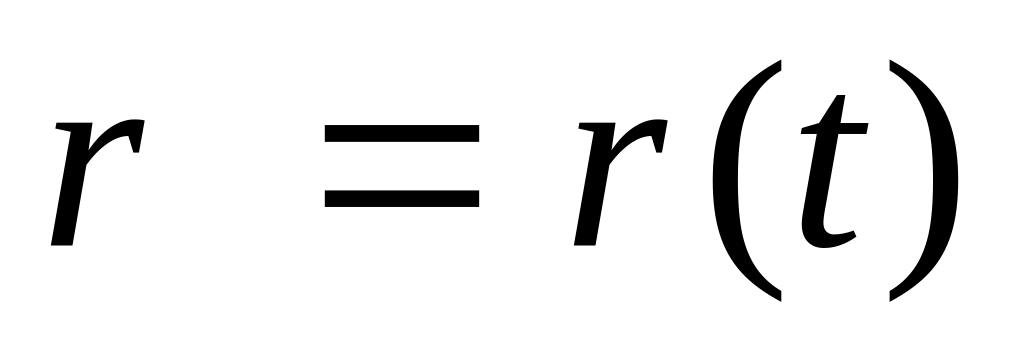Нехай точка рухається відносно системи за законом . Приймаючи за початок радіуса-вектора рухомої точки початок системи координат, можна записати згідно (1.5) 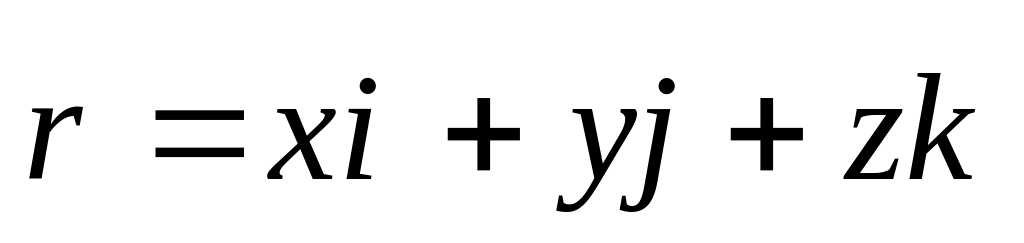. Тоді 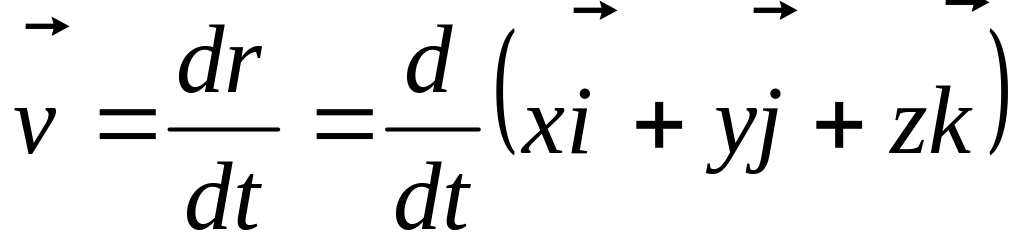. Так як орти незмінні, то отримаємо

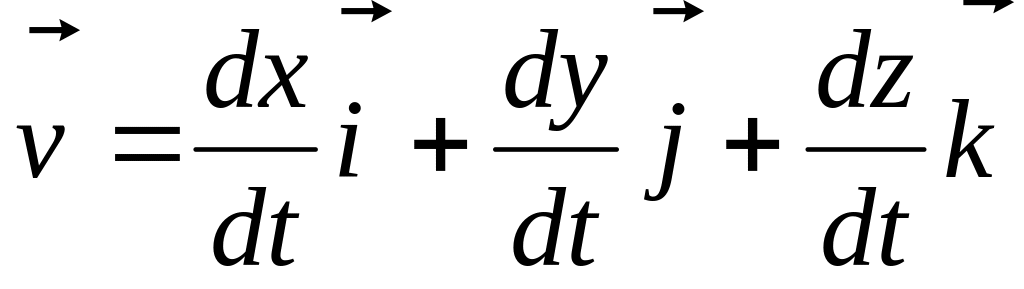. (1.13)

Оскільки швидкість 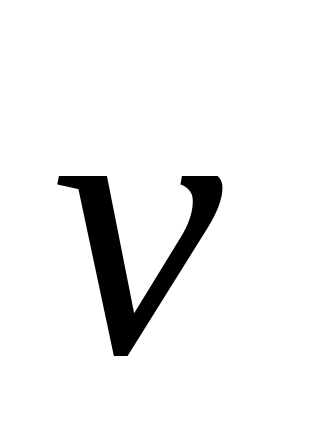є вектор, то його можна розкласти на три складові вектори, які паралельні осям координат.

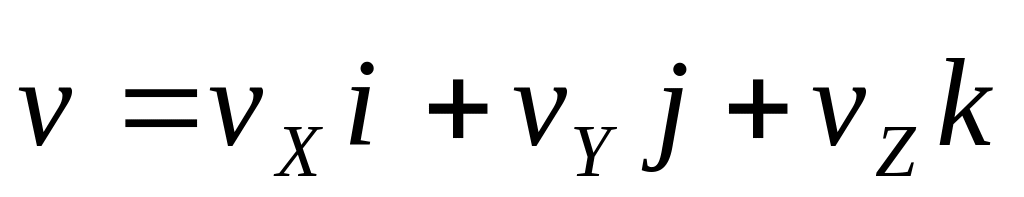. (1.14)

Порівнюючи (1.13) і (1.14), маємо:

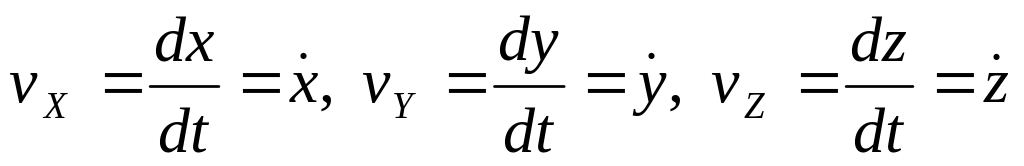. (1.15)

Проекція швидкості точки на яку-небудь координату вісь дорівнює похідній по часу від відповідної координати точки.

Маючи проекцію швидкості точки на осі координат, можна знайти модуль і напрям вектора швидкості:

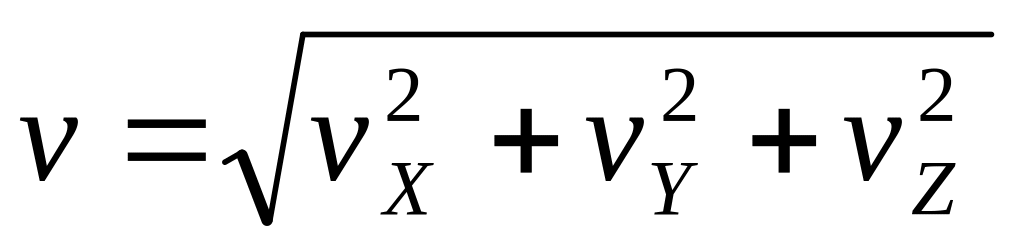, (1.16)

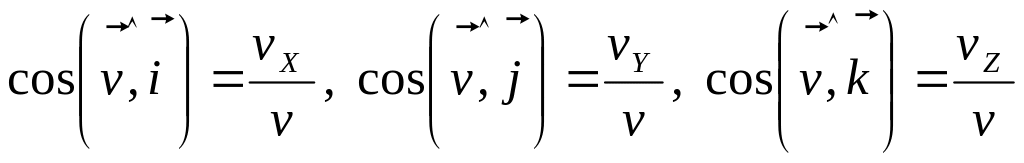. (1.17)

Аналогічно для прискорення можна отримати

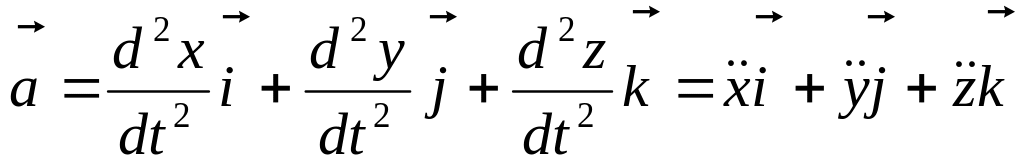. (1.18)

З іншого боку вектор прискорення 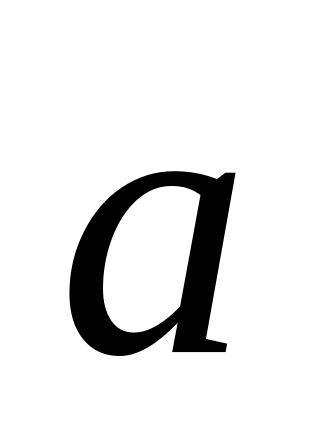можна розкласти на три складові

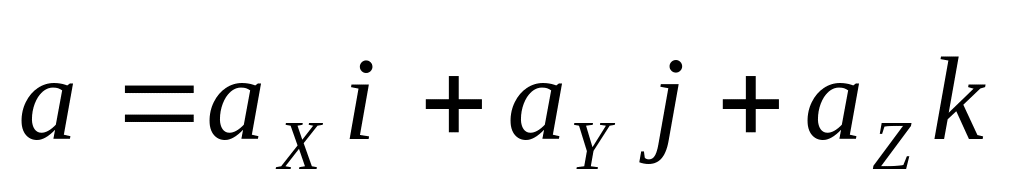, (1.19)

де 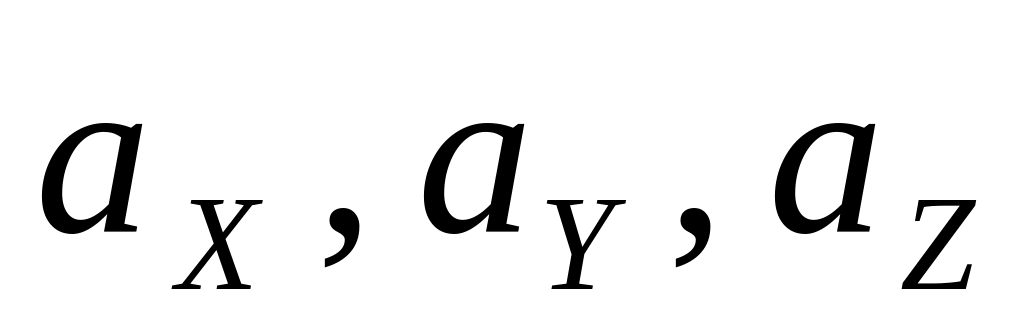– проекції прискорення на осі координат.

Порівнюючи (1.19) і (1.18), маємо:

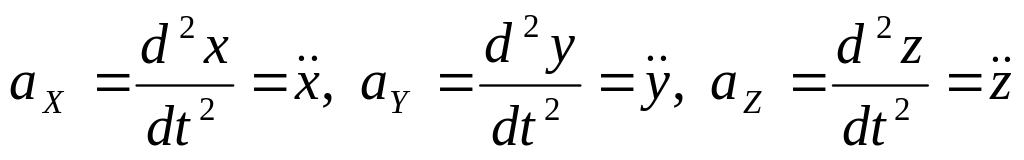. (1.20)

Маючи проекції прискорення точки на осі координат, можна знайти модуль і напрям вектора прискорення:

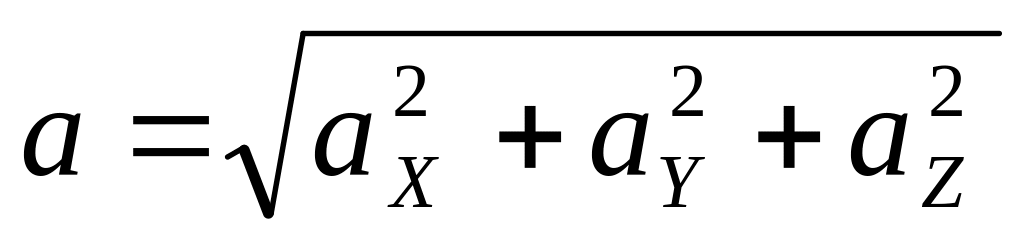, (1.21)

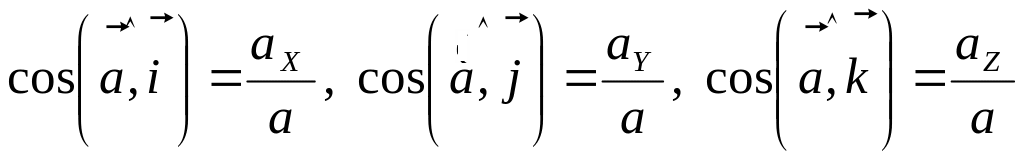_{. (1.22)}