Теоретические основы начертательной геометрии

Позиционные задачи

Геометрически закономерное изображение пространственного объекта на плоскости достигается при помощи метода проецирования, который является основным методом в начертательной геометрии и инженерной графике [1].

Позиционными называют задачи, свя­занные с решением на комплексном чер­теже вопросов взаимного расположения геометрических объектов. Наибольший прак­тический интерес здесь представляют две группы задач: задачи на взаимную при­надлежность и задачи на взаимное пере­сечение.

Точка принадлежит плоскости, если она принадлежит линии плоскости; прямая ли­ния принадлежит плоскости, если две ее точ­ки принадлежат плоскости.

Точка принадлежит поверхности, если она принадлежит конкретной линии поверх­ности.

Поверхности вращения

Поверхности вращения нашли самое широкое применение в технике. Они огра­ничивают поверхности большинства маши­ностроительных деталей.

«Зеленую улицу» для их внедрения обеспечила простота форми­рования. Эти поверхности образуются вра­щением криволинейной или прямолинейной образующей m вокруг неподвижной прямой оси i

(рис.1). На чертеже ось поверхности вращения обычно располагают перпендикулярно од­ной плоскости проекций.

Геометрическая часть определителя по­верхности вращения

состоит из этих двух линий: образующей m и оси i. Каждая точка образующей при вра­щении описывает окружность (параллель), плоскость

ко­торой перпендикулярна оси вращения. Так создается каркас поверхности, со­стоящий из множества окружностей. Наименьшую парал­лель называют горлом, наибольшую - эква­тором.

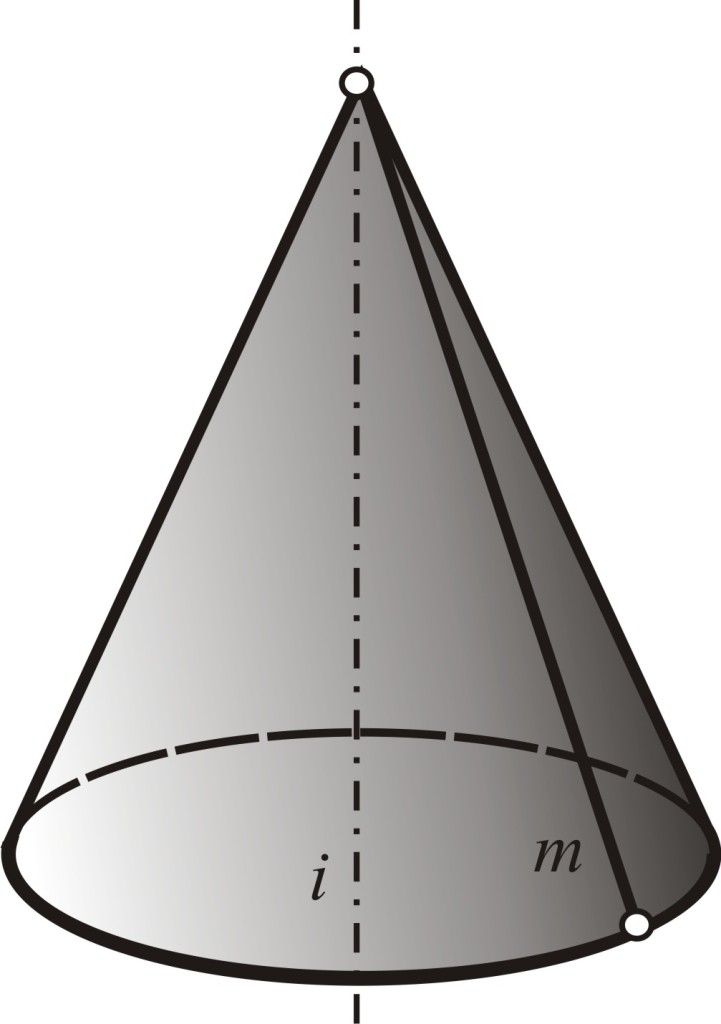
	Рис.2. Конус вращения
Рис.1. Поверхность вращения	Рис.3. Цилиндр вращения

Кривые на поверхности вращения, об­разующиеся в результате пересечения по­верхности плоскостями, проходящими через ось вращения,

называются меридианами. Все меридианы одной поверхности конгру­энтны. Фронтальный меридиан называют главным меридианом, он

определяет фрон­тальный очерк поверхности вращения.

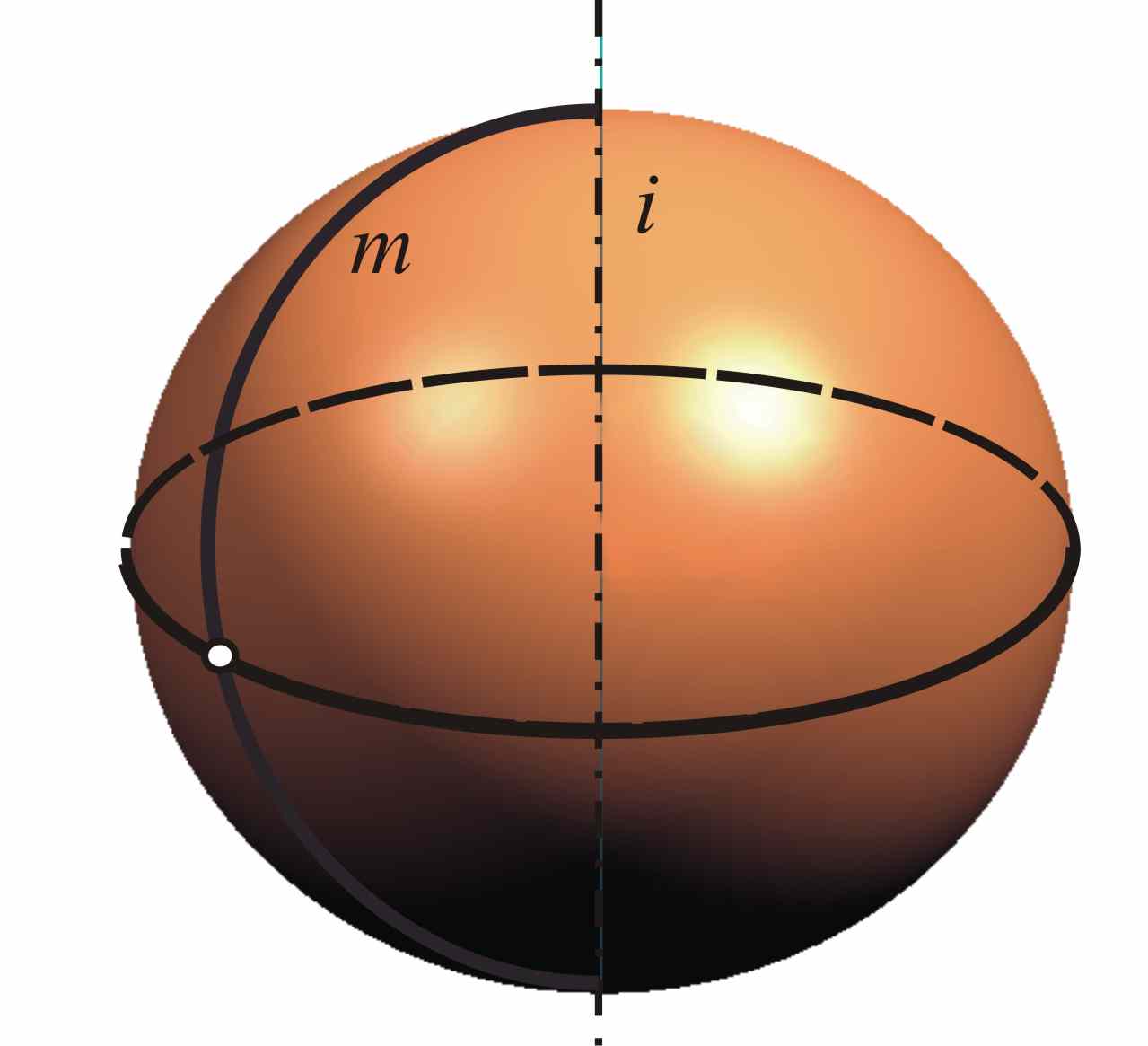
Рис.4. Сфера

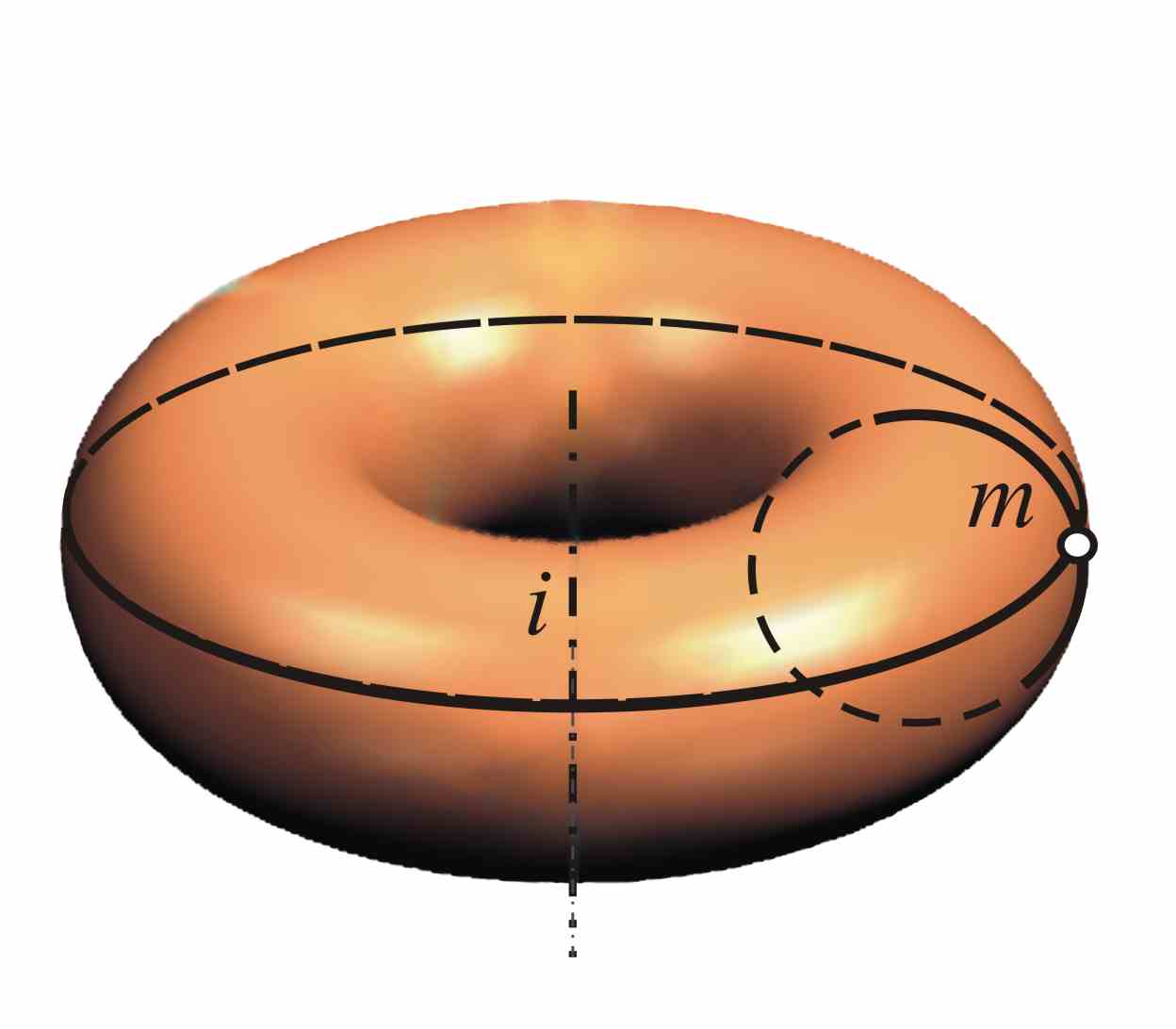
Рис.5. Тор

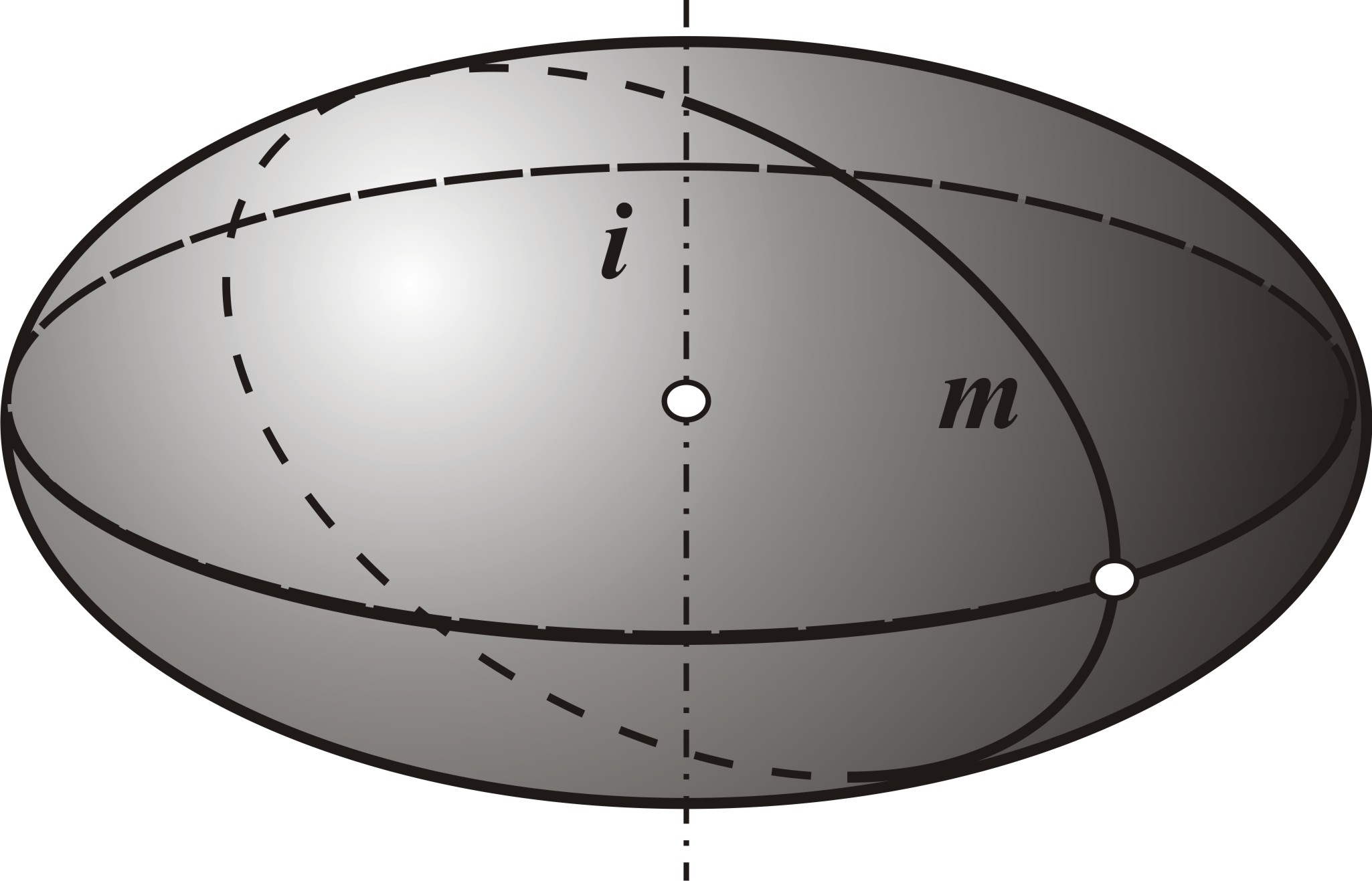
Рис.6. Эллипсоид вращения

Коническая поверхность вращения об­разуется вращением прямой m вокруг пере­секающейся с ней прямой — оси i (рис.2). Эту поверхность называют еще конусом вращения или прямым круговым конусом.

Цилиндрическая поверхность враще­ния образуется вращением прямой m вок­руг параллельной ей оси i (рис.3). Эту поверхность называют еще цилиндром вра­щения или прямым круговым цилиндром.

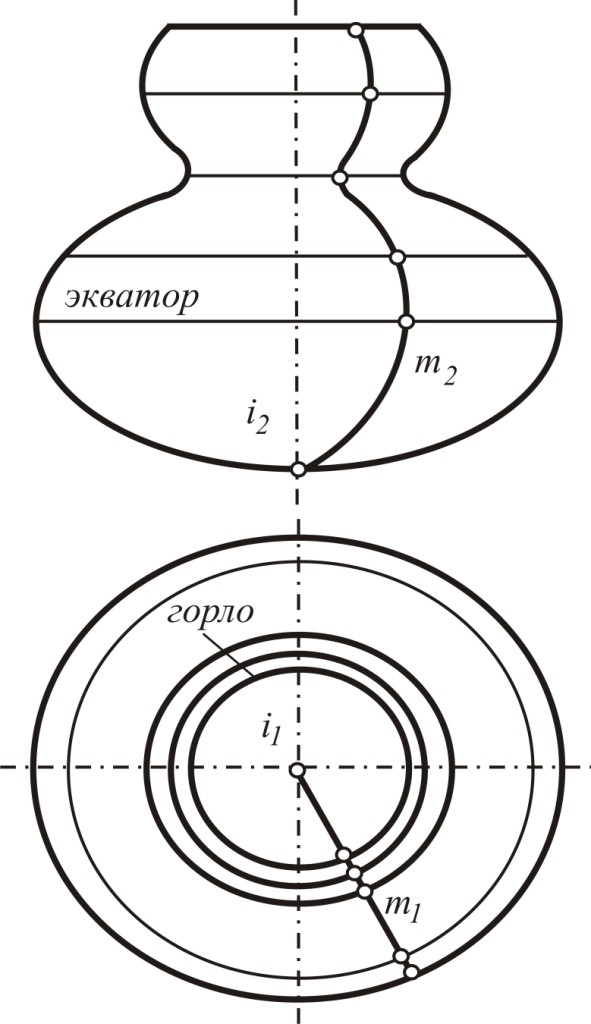
Сфера образуется вращением окруж­ности m вокруг прямой i (рис.4).

Тор образуется вращением окружности или ее дуги вокруг оси, лежащей в плоскости окружности. Если ось расположена в пределах образующей окружности, то такой тор называется закрытым. Если ось вращения находится вне окружности, то такой тор называется от­крытым (рис.5). Открытый тор назы­вают еще кольцом.

Поверхности вращения могут быть об­разованы и другими кривыми второго по­рядка.

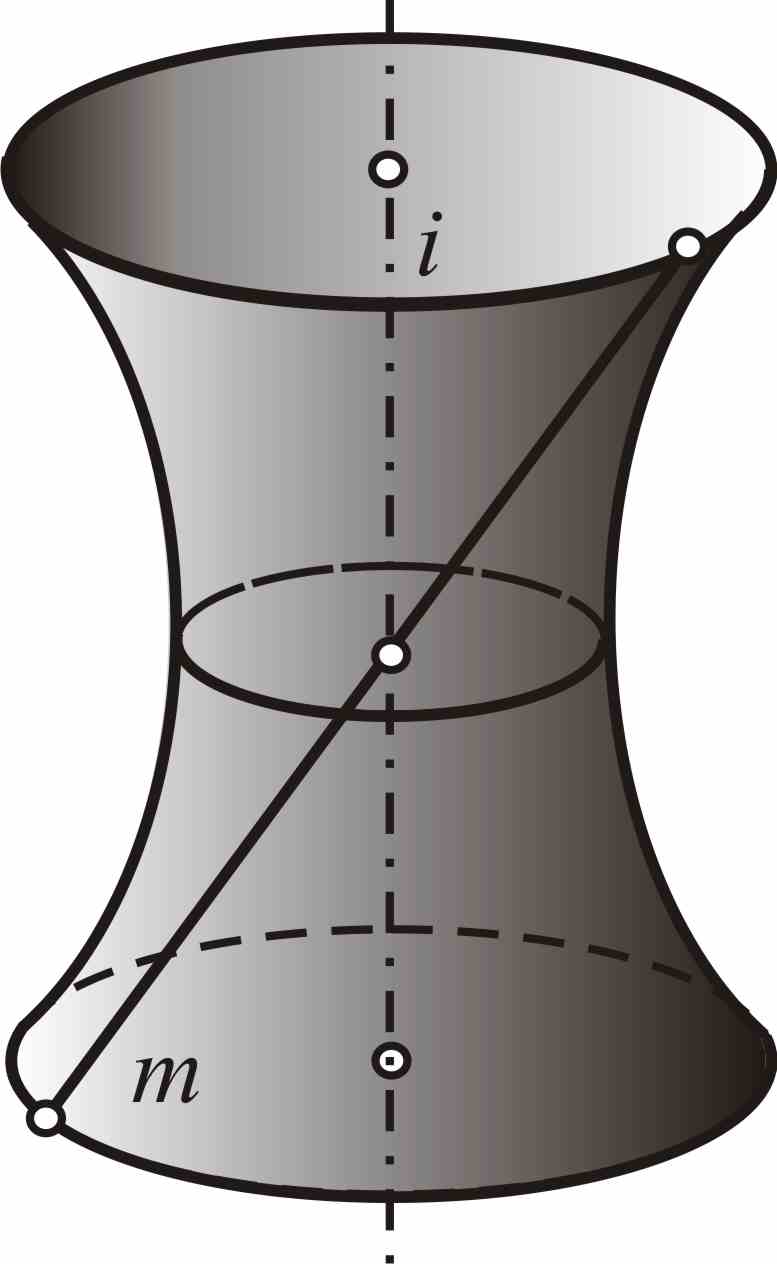
Эллипсоид вращения (рис.6) образуется вращением эллипса вокруг од­ной из его осей; параболоид вращения (рис.7) - вращением параболы вок­руг ее оси; гиперболоид вращения однополостный (рис.8) образуется враще­нием гиперболы вокруг мнимой оси, а двуполостный - вращением гиперболы вокруг действительной оси.

Рис.7. Параболоид вращения	Рис.8. Гиперболоид вращения

Линейчатые поверхности

Линейчатой называют поверхность, которая образуется движением прямой линии (образующей) в пространстве по определённому закону [1].

Линейчатые поверхности с одной направляющей.

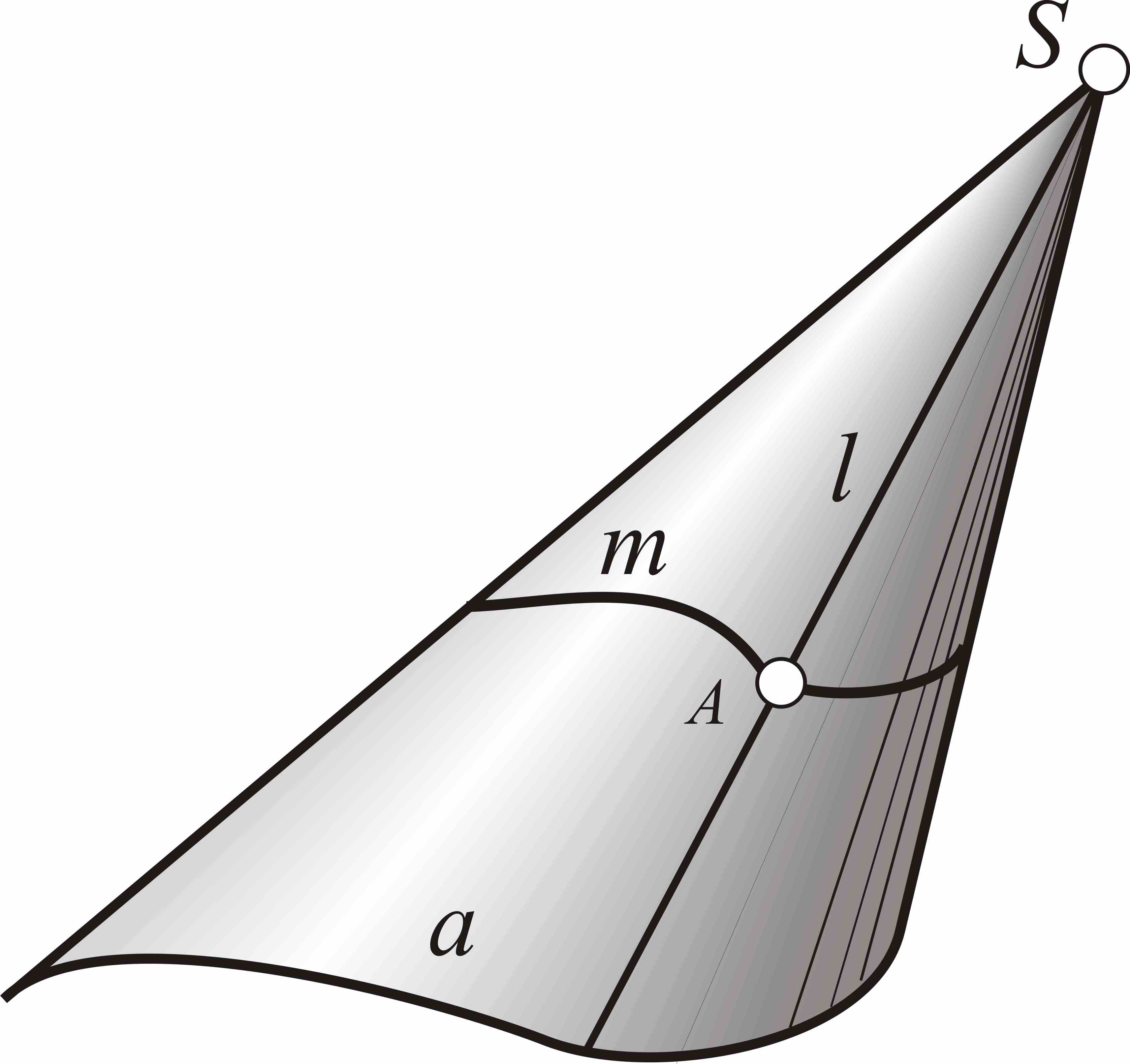
Коническая поверхность образуется перемещением прямолинейной образующей l по криволинейной направляющей a. При этом одна точка образующей всегда не­подвижна и является вершиной кони­ческой поверхности (рис.9). Опреде­литель конической поверхности включает вершину S и направляющую a.

Цилиндрическая поверхность образует­ся перемещением прямой l, пересекающей кривую нап­равляющую a и параллельно заданному направлению S (рис.10). Цилиндри­ческую поверхность можно рассматривать как частный случай конической поверхности с бесконечно удаленной вершиной.

Определитель цилиндрической поверх­ности состоит из направляющей a и нап­равления S.

Т

Рис.9. Коническая поверхность

Рис.10. Цилиндрическая поверхность

Рис.11. Торс

орсом называется поверхность, обра­зованная перемещением прямолинейной образующей l ,касающейся при своем движении во всех своих положениях некоторой пространст­венной кривой т, называемой ребром воз­врата (рис.11). Ребро возврата пол­ностью задает торс и является геомет­рической частью определителя поверх­ности.

Линейчатые поверхности с плоскостью параллелизма

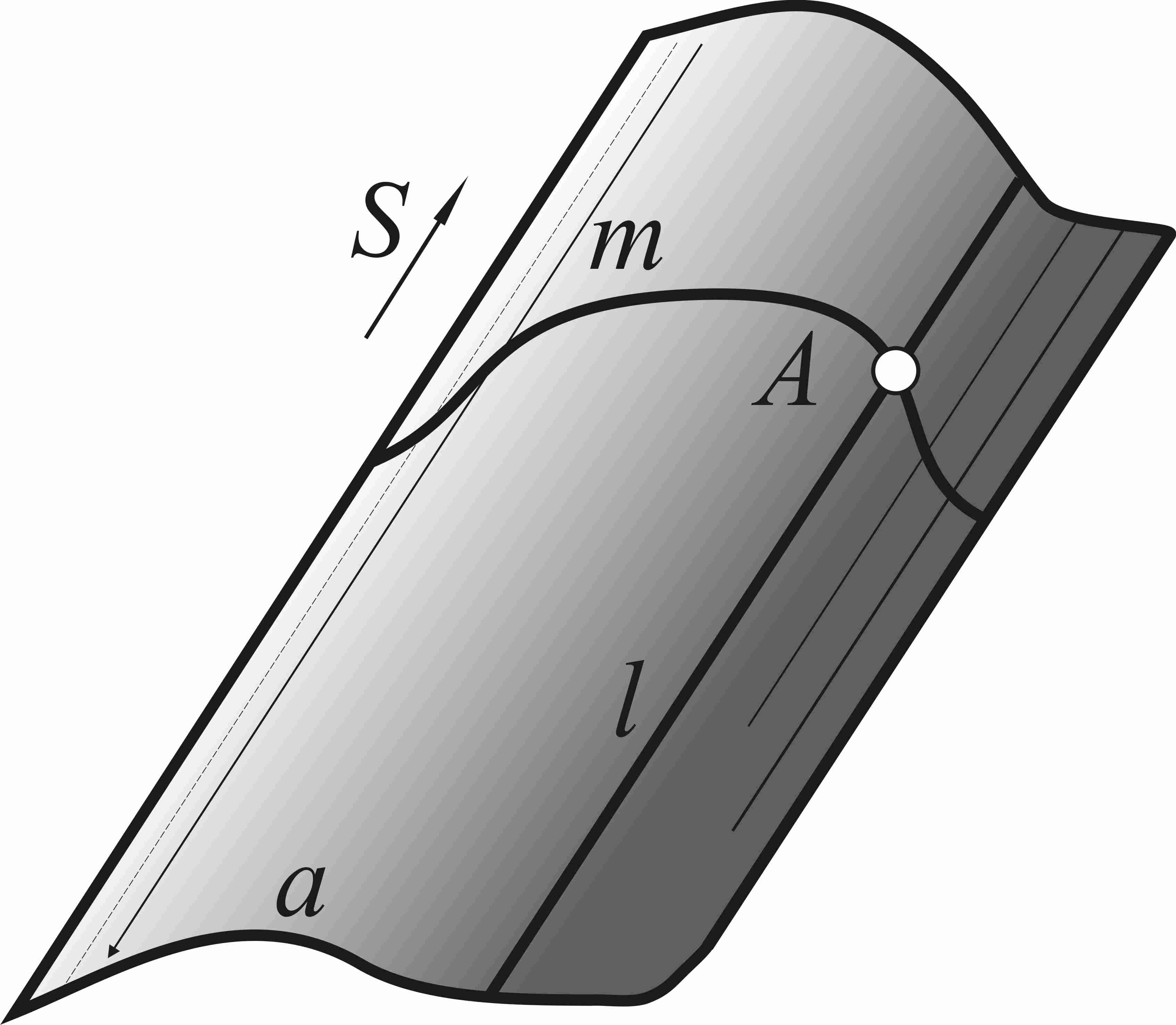
Поверхности с плоскостью параллелиз­ма представляют собой множество прямых (образующих), параллельных некоторой плоскости (плоскости параллелизма) и пересекающих две данные линии - на­правляющие.

Если направляющими являются две кривые линии, то поверхность называется цилиндроидом. Если одна из направ­ляющих — прямая линия, а вторая — кри­вая, то поверхность называется конои­дом и, наконец, если обе направляю­щие — прямые линии, то поверхность называют гиперболическим пара­болоидом или косой плоскостью.

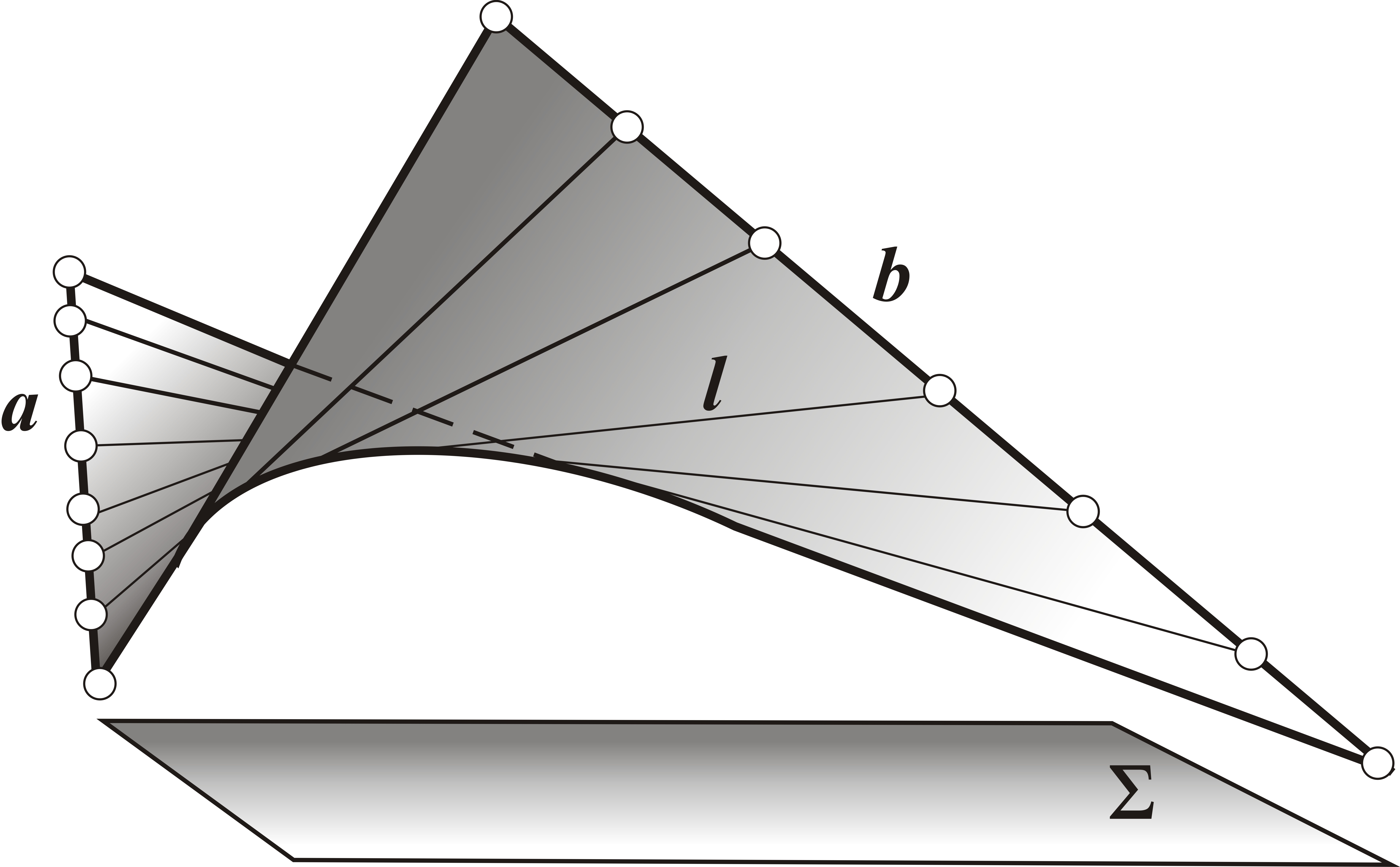
Поверхность цилиндроида определяется плоскостью параллелизма Σ (рис.12) и двумя криволинейными направляющими a и b, которые могут быть пространствен­ными кривыми или плоскими. В последнем случае

Рис.12. Цилиндроид	Рис.13. Коноид

плоскости, в которых расположены направляющие, не должны совпадать друг с другом. Прямая линия l, оставаясь параллельной заданной плоскости Σ, при своем движении по направляющим образует поверхность цилиндроида.

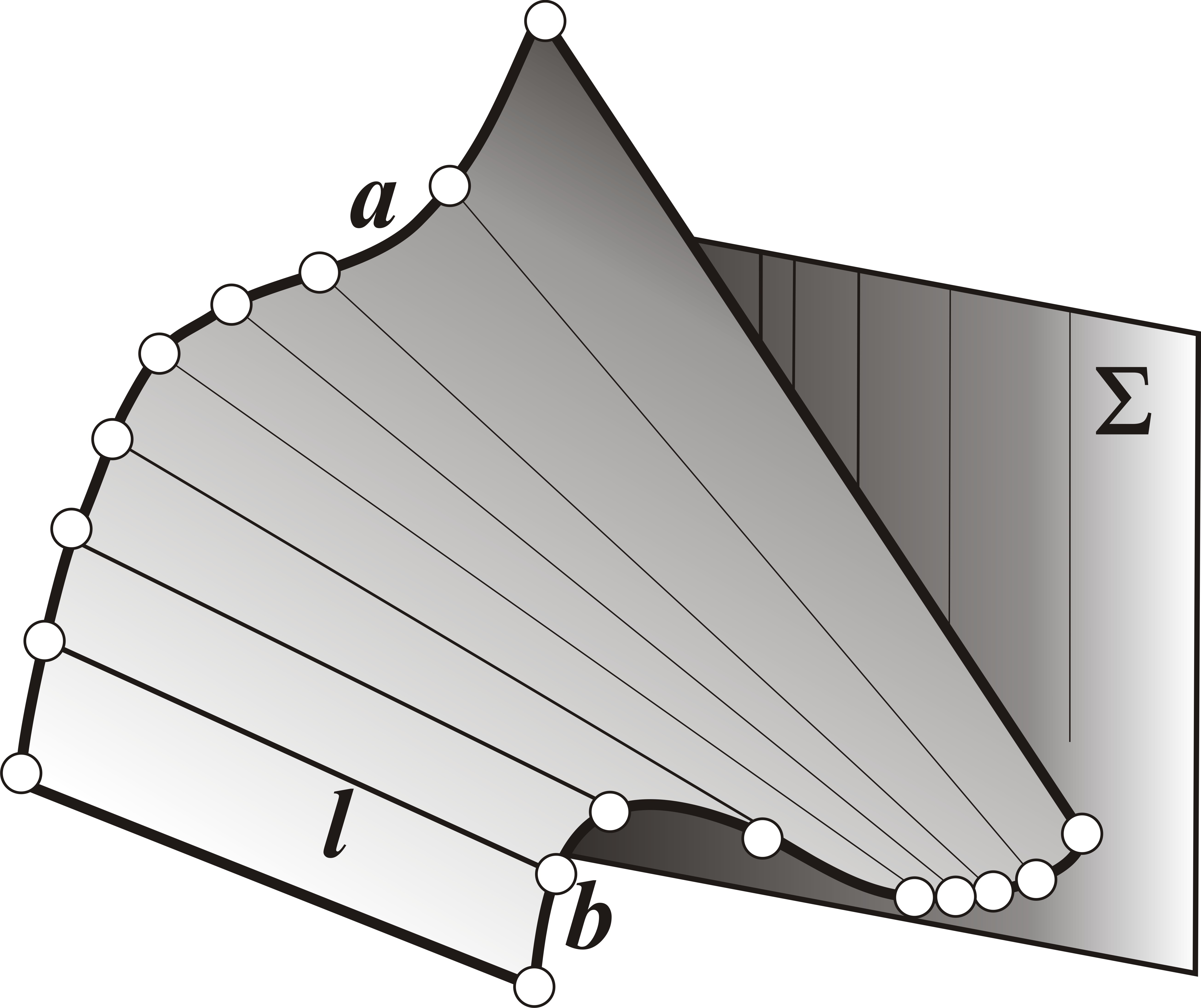
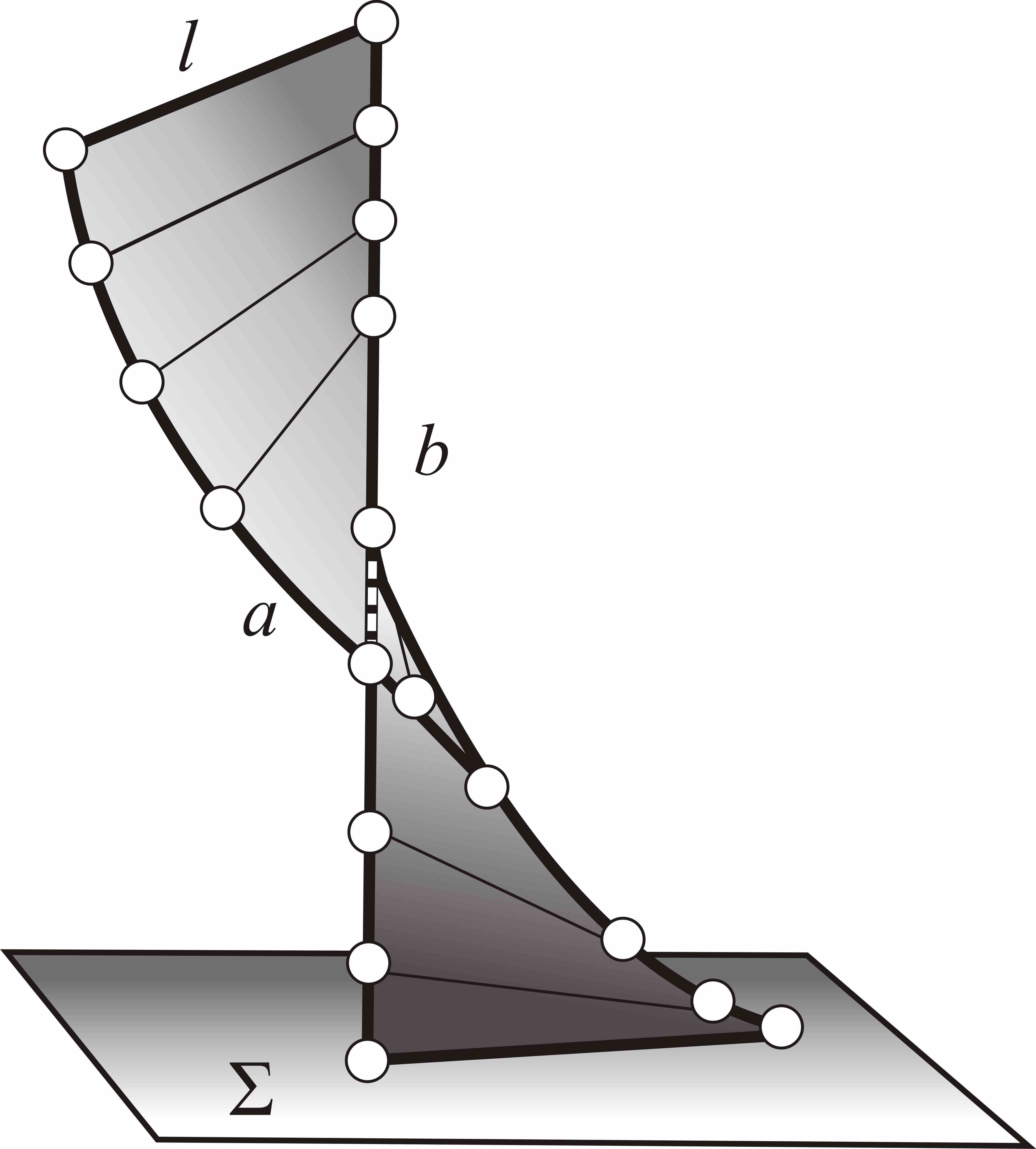
Коноид и гиперболический параболоид отличаются от цилиндроида лишь видом направляющих, которые входят в набор постоянных элементов геометрических час­тей определителей рассматриваемых по­верхностей. У коноида – прямая и кривая (рис.13), а у косой плоскости две прямые (рис.14).

Рис.14. Косая плоскость