МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ “ЛЬВІВСЬКА ПОЛІТЕХНІКА"

Лабораторна робота № 3

з дисципліни ЕММ на тему:

«Виробнича регресія»

Варіант № 1

Виконала:

ст. гр. ОА-31

Атаманчук О.І.

Перевірила:

Князевська О.В.

Львів 2011

Мета: оцінити параметри виробничої регресії Кобба-Дугласа, оцінити адекватність моделі статистичним даним генеральної сукупності за допомогою критерію Фішера, визначити частинні коефіцієнти еластичності та сумарний коефіцієнт еластичності, визначити прогнозне значення та інтервал довіри для прогнозу, побудувати ізокванти.

Завдання:

За даними табл. 3.1 з ймовірністю 0,95, використовуючи метод найменших квадратів, необхідно:

Таблиця 3.1

Статистичні дані

Працезатрати (x1), у.г.о.	Основні засоби (x2), у.г.о.	Обсяг виготовленої продукції (y), у.г.о.
30,1	50,2	78,2
30,7	53,5	82,5
33,7	53,1	83,9
35,2	56,5	86,7
36,4	54,1	87,0
39,4	58,2	92,8
41,8	55,1	91,6
40,4	57,2	95,3
44,2	56,1	94,7
46,0	55,2	92,8
47,8	57,1	99,5
49,5	58,7	102,9
49,7	58,1	102,6
50,0	58,1

1. оцінити параметри виробничої регресії Кобба-Дугласа, що має вигляд

;

2. оцінити адекватність побудованої моделі статистичним даним генеральної сукупності за допомогою критерію Фішера;

3. визначити частинні коефіцієнти еластичності та сумарний коефіцієнт еластичності;

4. визначити прогнозне значення та інтервал довіри для прогнозу;

5. побудувати ізокванти при у=у₃ та у=у₁₀.

Хід роботи:

1. Для оцінки параметрів лінії регресії прологарифмуємо рівняння і виконаємо заміну величин:

.

Заміна . Отримаємо

.

Використовуючи метод найменших квадратів, отримаємо систему нормальних рівнянь

,

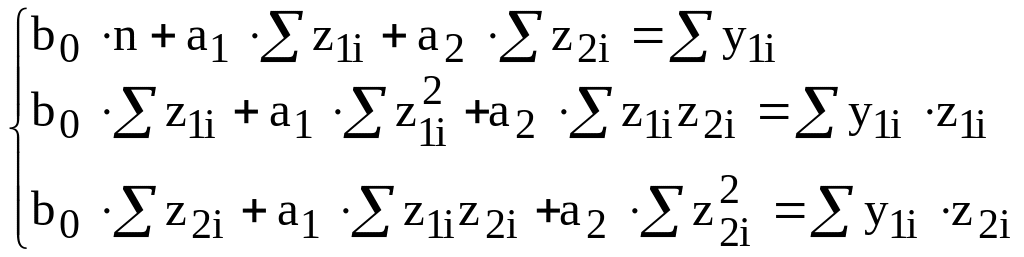з якої визначаємо параметри моделі b₀ , а_1,a₂ матричним методом :

n ∑lnx₁ ∑lnx₂ ∑lny b₀ ∑lnx₁ ∑lnx₁² ∑lnx_1* lnx₂ × ∑lny *lnx₁ = a₁

∑lnx₂ ∑lnx_1* lnx₂ ∑ lnx₂² ∑lny *ln x₂ a₂

Для того щоб визначити ці параметри, необхідно знайти показники, які записуємо в таблиці 3.2:

Таблиця 3.2

	lnX1	lnX2	lnY	lnX1*lnX1	lnX1*lnX2	lnX2*lnX2	lnY*lnX1	lnY*lnX2
1	3,405	3,916	4,359	11,591	13,332	15,335	14,841	17,071
2	3,424	3,980	4,413	11,726	13,627	15,838	15,111	17,562
3	3,517	3,972	4,430	12,373	13,972	15,778	15,581	17,595
4	3,561	4,034	4,462	12,681	14,366	16,275	15,891	18,003
5	3,595	3,991	4,466	12,921	14,345	15,927	16,053	17,823
6	3,674	4,064	4,530	13,497	14,930	16,515	16,644	18,411
7	3,733	4,009	4,517	13,935	14,966	16,073	16,863	18,111
8	3,699	4,047	4,557	13,681	14,968	16,375	16,856	18,440
9	3,789	4,027	4,551	14,354	15,258	16,218	17,241	18,326
10	3,829	4,011	4,530	14,658	15,357	16,088	17,345	18,171
11	3,867	4,045	4,600	14,954	15,641	16,360	17,789	18,607
12	3,902	4,072	4,634	15,225	15,891	16,585	18,081	18,871
13	3,906	4,062	4,631	15,257	15,867	16,501	18,088	18,811
Разом	47,900	52,230	58,681	176,853	192,519	209,868	216,384	235,802

Підставляємо отримані результати в формулу (матрицю) для отримання параметрів b₀ , а_1,a_{2 :}

1 3	47,8998	52,2300
47,8998	176,8526	192,5192
52,2300	192,5192	209,8682

58,681	b0
216,384	= a1
235,802	a2

- 1

*

Обертаємо матрицю:

1 3	47,8998	52,2300
47,8998	176,8526	192,5192
52,2300	192,5192	209,8682

1 210,086	61,634	-357,694
61,634	7,169	-21,915
-357,694	-21,915	109,128

-1

==

Перемножуємо отримані матриці:

1 3	47,8998	52,2300
47,8998	176,8526	192,5192
52,2300	192,5192	209,8682

58,681	0,560
216,384	= 0,331
235,802	0,681

- 1

*

a₀=e^b0, a₀=1,751

Виробнича регресія Кобба-Дугласа матиме вигляд:

y=1,751*x₁^0,331*x₂^0,681.

2. Визначаємо та оцінюємо адекватність побудованої моделі за допомогою критерія Фішера (F-критерій) та Дарбіна-Уотсона( за даними табл. 3.3)

F=

F_кр = 4,67 (за статистичними таблицями з ймовірністю 0,95);

172,477>4,67; F> F_кр . Отже модель адекватна.

Критерій Дарбіна-Уотсона:

d= _,

_{де ut=yt-y}^{^}_t

3. Частинний коефіцієнт еластичності для фактора обчислюється за формулою

Для виробничої регресії Кобба-Дугласа отримаємо

, =0,331.

. Цей показник називають загальним (сумарним) коефіцієнтом еластичності. На основі отриманих формул можна зробити висновок:

а=1,012, отже, збільшення факторів в разів викличе збільшення обсягу в разів. В даному випадку маємо економію ресурсів на масштабах виробництва.

4. Точкову оцінку прогнозу знайдемо за формулою

= 1,751*50 ^0,331*58,1 ^0,681= 101,434

Інтервал довіри знаходять спочатку для лінійної регресії, а потім шляхом потенціювання – для нелінійної регресії:

,

,

,

де t – значення t-критерію при ймовірності р і n-m-1 ступенях вільності; t=1,77.

- середньоквадратичне відхилення залишків;

1210,086	61,634	-357,694
61,634	7,169	-21,915
-357,694	-21,915	109,128

* 1

3,912

4,062

=

-1,813

0,656

-0,131

= =

1

3,912

4,062

-1,813

0,656

-0,131

=

= 0,220

.

=1,77* 1,394* = 2,725

=4,619.

Знаходимо інтервал довіри:

101,434+2,725=103,559

101,434-2,725= 99,308,

Отже, інтервал довіри для прогнозу матиме вигляд:

103,559< < 99,308

5. Будуємо ізокванти при у = у₃ та при у = у₁₀.

Таблиця 3.3