1.2 Минимизация функций методом наискорейшего спуска
Одним из самых распространенных методов минимизации функции нескольких переменных является метод градиентного спуска. В этом методе в качестве направления поиска минимума заданной функции выбирается вектор, направление которого противоположно направлению вектора градиента функции F(X), где X={x1, x2, x3, … xn}. Координаты этого вектора :
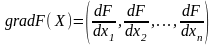
В математическом анализе доказывается, что вектор gradF(X) характеризует направление наиболее быстрого возрастания функции. Поэтому вектор – gradF(X) (антиградиента) является направлением наиболее быстрого ее убывания. Каждое последующее приближение получается из предыдущего смещением в направлении антиградиента функции F(X) (смотри рис.1).
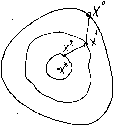
Рис. 1
Задавшись начальным приближением X0 ищется следующее приближение с помощью реккурентного соотношения вида:
,
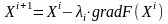i=0,1,2…
Приведенное соотношение не определяет алгоритм однозначно, поскольку ничего не сказано о выборе параметра li. Например его можно определять из условия минимума величины:
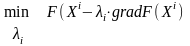
В этом случае рассматриваемый метод называют методом наискорейшего градиентного спуска, или просто методом наискорейшего спуска.
Рассматриваемая функция является функцией одного параметра l и ее минимум находится или методами одномерной минимизации или решением уравнения, которое имеет вид:
,
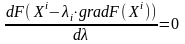минимальный неотрицательный корень этого уравнения и является искомым значением l i.
Поиск
прекращается при выполнении условия
,
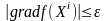так как градиент в точке минимума функции
= 0, а при приближенных вычислениях
.
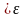2. Методика решения задачи
2.1 Алгоритм метода наискорейшего спуска
Подбирается для тестирования функция
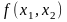.Задается точность e и шаг h для аппроксимации частных производных.
Задается любое начальное (
)
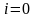приближение
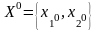
Определяются координаты вектора антиградиента минимизируемой функции в точке спуска
:
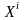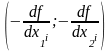методом
аппроксимации частных производных и
его модуль
Если , то поиск прекращается, так как градиент в точке минимума функции=0, а при приближенных вычислениях .
В направлении антиградиента ищется минимум функции
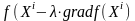одной переменной l.Находится следующее приближение
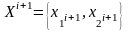по формулам:
.
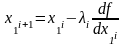
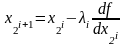
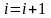Поиск повторяется с п. 3
2.2 Вычислительная схема
3. Блок-схемы алгоритма
Приведем пример общей блок-схемы для функций с «p» переменных.
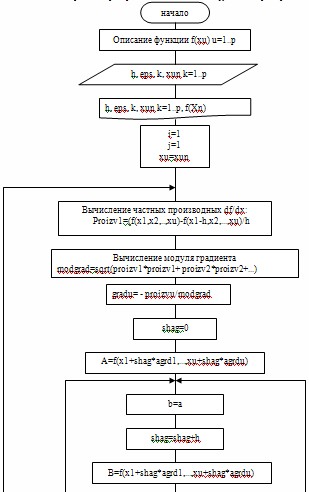
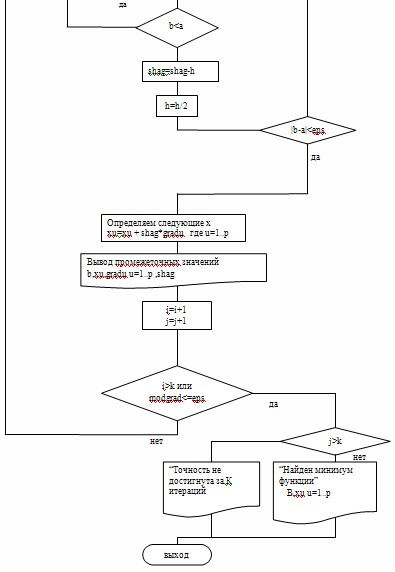
4. Текст программы на языке Pascal
функция переменная минимум спуск
1) Приведу пример программы для блок-схемы описанной в предыдущем пункте применимо к функции с одной переменной.
program p1;
function f(x:real):real;
begin
f:=(x-3)*(x-3)+2;
end;
var
k,i,j:integer;
x0,x,h,eps:real;
grad:real;
proizv,a,b,shag:real;
begin
writeln;
writeln('Введите начальные данные:');
writeln;
writeln('Введите h,eps,k');
readln(h,eps,k);
writeln('шаг h=',h:6:4,' точность eps=',eps:8:5,' число итераций k=',k);
writeln(''Введите Начальное приближение (x0)');
readln(x0);
write(' Начальные данные:');
write(' x0=',x0:9:5);
writeln('f(x0)=',f(x0):15:8);
writeln;
writeln('Результаты счёта:');
writeln;
writeln('Итер.: (xn) : анти-градиент : шаг : (xk) : f(xk) :');
writeln('----------------------------------------------------------------------');
j:=1;
i:=1;
x:=x0;
repeat
proizv:=(f(x)-f(x-h))/h;
grad:=-(f(x)-f(x-h))/h;
write(i:2,'(',x:8:3,') (',grad:2:4,') ');
shag:=0;
a:=f(x+shag*grad);
repeat
repeat
b:=a;
shag:=shag+h;
a:=f(x+shag*grad);
until b<a;
shag:=shag-h;
h:=h/2;
until abs(a-b)<=eps;
x:=x+shag*grad;
writeln(' ',shag:4:4,' (',x:4:3,') ',b:5:8);
readln;
if (grad<=eps) then
begin
i:=k+1;
writeln('Минимум функции найден:',b:5:8,' (',x:4:3,')');
end
else
begin
i:=i+1;
j:=j+1;
end;
until i>k;
if (j>k) then
writeln('Точность не достигнута за к =',k:3,' итераций');
readln;
end.
Исходные данные:
f = (x-2)*(x-2) + 1
шаг h = 0.1 точность eps = 0.001
кол-во итераций k =30
Начальное приближение:
x0 = 0.00000
f(x0)= 5.00000000
Результаты тестирования:
Итер. |
(xn) |
-вектор-градиент |
шаг |
(xk) |
f(xk) |
1 |
(0.000) |
(4.1) |
0.5998 |
2.459 |
1.21086392 |
2 |
(2.459) |
(-0.9183) |
0.5001 |
2.000 |
1.00000000 |
Найден минимум функции:
1.0000000 (2.000)
2) Теперь приведу пример программы для поиска минимума функции двух переменных.
program p2;
function f(x1,x2:real):real;
begin
f:= x1*x1-2*x1+16*x2*x2-32*x2+18;
end;
var
k,i,j:integer;
x10,x20,x1,x2,h,eps:real;
grad1,grad2,modgrd:real;
proizv1,proizv2,a,b,shag:real;
begin
writeln;
writeln('Введите начальные данные:');
writeln;
write('Введите шаг h=');
readln(h);
write('Введите точность eps=');
readln(eps);
write('Введите число итераций k=');
readln(k);
writeln('шаг h=',h:6:4,' точность eps=',eps:8:5,' число итераций k=',k);
writeln;
writeln('Введите Начальное приближение (x10,x20)');
write('x10=');
readln(x10);
write('x20=');
readln(x20);
write(' Начальное приближение и значение в этой точке функции:');
write(' x10=',x10:9:5,' x20=',x20:9:5);
writeln('f(x10,x20)=',f(x10,x20):15:8);
writeln;
writeln('Результаты:');
writeln;
writeln('Итерация: (x1n,x2n) : -вектор градиент : модуль : шаг : (x1k,x2k) : f(x1k,x2k) :');
writeln('---------------------------------------------------------------------------');
j:=1;
i:=1;
x1:=x10;
x2:=x20;
repeat
proizv1:=(f(x1,x2)-f(x1-h,x2))/h;
proizv2:=(f(x1,x2)-f(x1,x2-h))/h;
modgrd:=sqrt(proizv1*proizv1+proizv2*proizv2);
grad1:=-proizv1/modgrd;
grad2:=-proizv2/modgrd;
write(i:2,'(',x1:8:3,',',x2:8:3,') (',grad1:2:4,',',grad2:2:4,') ',modgrd:5:4);
shag:=0;
a:=f(x1+shag*grad1,x2+shag*grad2);
repeat
repeat
b:=a;
shag:=shag+h;
a:=f(x1+shag*grad1,x2+shag*grad2);
until b<a;
shag:=shag-h;
h:=h/2;
until abs(a-b)<=eps;
x1:=x1+shag*grad1;
x2:=x2+shag*grad2;
writeln(' ',shag:4:4,' (',x1:4:3,',',x2:4:3,') ',b:5:8);
readln;
if (modgrd<=eps) then
begin
i:=k+1;
writeln('найден минимум функции в точке:',b:5:8,' (',x1:4:3,',',x2:4:3,')')
end
else
begin
i:=i+1;
j:=j+1;
end;
until i>k;
if (j>k) then
writeln('Точность не достигнута за к=',k:3,' итераций');
readln;
end.
Исходные данные:
f1 = x1*x1-2*x1+16*x2*x2-32*x2+18
шаг h = 0.0001 точность eps = 0.00100
кол-во итераций k = 100
Начальное приближение:
x10 = -9.00000 x20 = 2.00000
f(x10,x20)= 117.00000000
Результаты тестирования:
Итер |
(x1n,x2n) |
-вектор-градиент |
модуль градиента |
шаг |
(x1k,x2k) |
f(x1k,x2k) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
(-9.0000, 2.0000) (-8.1516, 0.6425) (-6.3963, 1.7396) (-5.7687, 0.7356) (-4.4707, 1.5470) (-4.0065, 0.8044) (-3.0463, 1.4046) (-2.7030, 0.8553) (-1.9932, 1.2991) (-1.7392, 0.8929) (-1.2143, 1.2212) (-1.0263, 0.9208) (-0.6381, 1.1636) (-0.4990, 0.9414) (-0.2120, 1.1210) (-0.1091, 0.9566) (0.1030, 1.0895) (0.1792, 0.9679) (0.3362, 1.0662) (0.3926, 0.9762) (0.5087, 1.0490) (0.5504, 0.9824) (0.6362, 1.0362) (0.6672, 0.9869) (0.7305, 1.0268) (0.7535, 0.9903) (0.8002, 1.0198) (0.8172, 0.9928) (0.8518, 1.0147) (0.8645, 0.9946) (0.8899, 1.0108) (0.8993, 0.9960) (0.9179, 1.0079) (0.9250, 0.9969) (0.9386, 1.0058) (0.9440, 0.9977) (0.9538, 1.0043) (0.9579, 0.9982) (0.9652, 1.0032) (0.9683, 0.9987) (0.9737, 1.0024) (0.9761, 0.9989) (0.9800, 1.0018) (0.9819, 0.9992) (0.9847, 1.0013) (0.9861, 0.9994) (0.9883, 1.0010) (0.9894, 0.9995) (0.9909, 1.0007) (0.9919, 0.9996) (0.9929, 1.0005) |
(0.5300, -0.8480) (0.8480, 0.5300) (0.5300, -0.8480) (0.8480, 0.5300) (0.5301, -0.8479) (0.8480, 0.5300) (0.5300, -0.8480) (0.8479, 0.5302) (0.5303, -0.8478) (0.8478, 0.5303) (0.5304, -0.8478) (0.8478, 0.5304) (0.5304, -0.8477) (0.8476, 0.5306) (0.5306, -0.8476) (0.8474, 0.5309) (0.5310, -0.8473) (0.8474, 0.5309) (0.5312, -0.8473) (0.8473, 0.5311) (0.5314, -0.8471) (0.8472, 0.5313) (0.5319, -0.8468) (0.8465, 0.5325) (0.5330, -0.8461) (0.8456, 0.5337) (0.5348, -0.8450) (0.8454, 0.5341) (0.5351, -0.8448) (0.8435, 0.5372) (0.5385, -0.8426) (0.8405, 0.5419) (0.5439, -0.8392) (0.8361, 0.5486) (0.5512, -0.8344) (0.8288, 0.5595) (0.5635, -0.8261) (0.8267, 0.5626) (0.5679, -0.8231) (0.8232, 0.5678) (0.5686, -0.8226) (0.8117, 0.5841) (0.5867, -0.8098) (0.7956, 0.6058) (0.6072, -0.7946) (0.8007, 0.5991) (0.6046, -0.7966) (0.7714, 0.6363) (0.6525, -0.7578) (0.7322, 0.6811) (0.6805, -0.7327) |
37.7353 21.5841 27.9090 15.9646 20.6411 11.8083 15.2679 8.7349 11.2896 6.4618 8.3502 4.7804 6.1765 3.5371 4.5685 2.6176 3.3783 1.9372 2.4997 1.4338 1.8495 1.0614 1.3679 0.7864 1.0114 0.5831 0.7475 0.4325 0.5540 0.3214 0.4091 0.2396 0.3019 0.1794 0.2229 0.1352 0.1642 0.1019 0.1228 0.0771 0.0925 0.0589 0.0683 0.0456 0.0506 0.0347 0.0389 0.0275 0.0280 0.0223 0.0209 |
1.6008 2.0699 1.1840 1.5308 0.8757 1.1323 0.6478 0.8371 0.4791 0.6191 0.3544 0.4579 0.2622 0.3386 0.1940 0.2503 0.1435 0.1852 0.1062 0.1370 0.0786 0.1013 0.0582 0.0748 0.0431 0.0552 0.0319 0.0409 0.0237 0.0301 0.0176 0.0221 0.0131 0.0162 0.0098 0.0118 0.0073 0.0088 0.0055 0.0066 0.0042 0.0048 0.0032 0.0035 0.0024 0.0027 0.0019 0.0019 0.0015 0.0014 0.0012 |
(-8.1516, 0.6425) (-6.3963, 1.7396) (-5.7687, 0.7356) (-4.4707, 1.5470) (-4.0065, 0.8044) (-3.0463, 1.4046) (-2.7030, 0.8553) (-1.9932, 1.2991) (-1.7392, 0.8929) (-1.2143, 1.2212) (-1.0263, 0.9208) (-0.6381, 1.1636) (-0.4990, 0.9414) (-0.2120, 1.1210) (-0.1091, 0.9566) (0.1030, 1.0895) (0.1792, 0.9679) (0.3362, 1.0662) (0.3926, 0.9762) (0.5087, 1.0490) (0.5504, 0.9824) (0.6362, 1.0362) (0.6672, 0.9869) (0.7305, 1.0268) (0.7535, 0.9903) (0.8002, 1.0198) (0.8172, 0.9928) (0.8518, 1.0147) (0.8645, 0.9946) (0.8899, 1.0108) (0.8993, 0.9960) (0.9179, 1.0079) (0.9250, 0.9969) (0.9386, 1.0058) (0.9440, 0.9977) (0.9538, 1.0043) (0.9579, 0.9982) (0.9652, 1.0032) (0.9683, 0.9987) (0.9737, 1.0024) (0.9761, 0.9989) (0.9800, 1.0018) (0.9819, 0.9992) (0.9847, 1.0013) (0.9861, 0.9994) (0.9883, 1.0010) (0.9894, 0.9995) (0.9909, 1.0007) (0.9919, 0.9996) (0.9929, 1.0005) (0.9937, 0.9996) |
86.79556740 64.45720228 47.93446521 35.71523586 26.67678836 19.99208346 15.04696284 11.39108929 8.68640754 6.68625352 5.20636207 4.11195235 3.30212499 2.70343298 2.26024138 1.93268856 1.69018046 1.51081645 1.37800772 1.27981375 1.20707634 1.15331690 1.11348831 1.08408924 1.06227753 1.04618463 1.03423639 1.02539864 1.01882734 1.01399489 1.01039152 1.00774673 1.00576726 1.00431662 1.00322468 1.00242801 1.00182378 1.00137608 1.00103492 1.00078339 1.00058875 1.00044920 1.00033973 1.00026157 1.00019896 1.00015311 1.00011610 1.00009048 1.00006927 1.00005451 1.00004175 |
Найден минимум функции:
f(x1n,x2n)= 1.00004175
Вывод
Данная программа не более чем за две итерации находит минимум простой функции (на первой она находит минимум, а на второй уточняет его) но для нахождения минимума сложной, т.е. «изогнутой» функции потребуется 10-ть и более итераций т.к. вектор антиградиент будет сильно менять направление.