Теория по ОАПЭЦ

можно записать для каждой ветви произвольной цепи. Таким образом, если цепь со- держит Q ветвей, то получится система из Q уравнений:

(2.23)

которая в матричной форме выглядит следующим образом:

I&B + J&B = YB (U&B + E&B ).

(2.24)

Исходя из уравнений (2.21) аналогичным путем получим

U&B + ĖB = ZB (I&B + J&B ).

(2.25)

Соотношения (2.24) и (2.25) представляют собой закон Ома в матричной форме.

2.6.1. Матричные уравнения контурных токов

Умножим обе части уравнения (2.25) на контурную матрицу В:

B(U&B + Ė) = BZB (I&B + J&B ).

Учитывая, что произведение BU&B равно нулю, так как выражает сумму на- пряжений на зажимах ветвей замкнутых контуров, получим

BZBI&B = B(E& − ZB J&).

(2.26)

Но токи ветвей IB можно выразить через контурные токи согласно (2.12), следовательно,

BZBBT I&K = B(E& − ZB J&).

(2.27)

Уравнение (2.27) является обобщением второго закона Кирхгофа и назы-

вается матричным уравнением электрического равновесия в контурных токах.

Правая часть этого уравнения выражает результирующее действие всех источ- ников в контурах. Тройное матричное произведение BZBBT в левой части пред- cтавляет собой квадратную матрицу и имеет порядок, равный числу независимых контуров. В этом нетрудно убедиться, учитывая, что матрица ZB является мат- рицей порядка Q, где Q – число ветвей, а матрица В имеет N строк и Q столб- цов, где N – число независимых контуров.

Тройное матричное произведение, называемое матрицей контурных со-

противлений, обозначим так:

Диагональный член матрицы контурных сопротивлений ZKK представляет собой сумму всех сопротивлений k–го контура, а недиагональный член ZKJ – сопротивление, общее для контуров k и j; знак этого сопротивления определя- ется направлениями контурных токов. Если направления контурных токов контуров k и j в ветви kj совпадают, то сопротивление ZKJ имеет положительный знак. В противном случае перед ZKJ ставится отрицательный знак.

Пример 2.3. Составить матрицу контурных сопротивлений для цепи, граф которой показан на рис. 2.14.

Решение. Составим контурную матрицу для заданного графа:

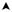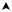III II

3 2

5

Затем найдем произведение матрицы сопротивлений ветвей ZВ и транспониро- ванной контурной матрицы ВT:

Наконец, определим тройное матричное произведение, равное матрице контурных сопротивлений:

Если в цепи имеются индуктивно связанные ветви, то матрицу сопротивле- ний ZB удобно разбить на подматрицы ZLM, r, ZC. Тогда тройное матричное про- изведение BZBBT может быть представлено в виде

(2.30)

то основное уравнение электрической цепи для контурных токов примет вид

(ZLM' + r' + ZC' )I&K = B(E& − ZB J&).

(2.31)

Вернемся к рассмотрению уравнения (2.27). Если подставить в левую часть этого уравнения значение тройного матричного произведения из (2.28) и записать его в развернутом виде, то получим систему уравнений контурных токов в той форме, в какой она обычно приводится в курсах ТОЭ:

(2.32)

Здесь Ė1ЭКВ , Ė2ЭКВ,..., ĖNЭКВ – эквивалентные ЭДС, соответствующие правой час-

ти (2.27). Каждая из них равна сумме ЭДС источников соответствующего кон- тура за вычетом суммы падений напряжений от токов источников тока.

Любой контурный ток системы уравнений (2.32) можно найти из выраже- ния Inn= n / , где определитель

а алгебраическое дополнение n получается из определителя путем замены п- го столбца на элементы матрицы ЕЭКВ (правая часть системы (2.32)). Разлагая

n по элементам n-го столбца (правило Крамера), получим

Здесь jn , j=1…N – алгебраические дополнения (адъюнкты) элемента jn опре- делителя . Уравнение (2.33) может быть также записано в виде

I&kn = Y1n (s)E&1Э + Y2n(s)E&2Э + ...+ YNn(s)E&NЭ ,

(2.34)

где Yjn(s)– частная функция проводимости.

2.6.2.Матричные уравнения узловых потенциалов

Втех случаях, когда число узлов меньше числа независимых контуров, целесообразно за искомые величины принять потенциалы узлов, приняв рав- ным нулю потенциал базисного узла.

Для составления матричных уравнений узловых потенциалов следует ис- пользовать узловую матрицу А, которая, как указывалось, может быть получена из

полной узловой матрицы А0 путем отбрасывания одной строки, соответствующей ба- зисному узлу. За базисный можно принять любой из узлов. Базисный узел будем нумеровать цифрой нуль. Поясним принцип составления уравнений узловых по- тенциалов на конкретном примере.

Составим узловую матрицу А для графа, изображенного на рис. 2.15:

Обозначим токи в ветвях через Im ( индекс m соответствует номеру ветви). Если

умножить токи ветвей на соответствующие элементы матрицы А и затем просум- мировать полученные произведения по строкам, то получим следующую систему уравнений:

+ I&1 - I&3 − I&7 = 0 üï −I&1 + I&2 − I&8 = 0ï + I&4 − I&6 + I&7 = 0ïý. −I&4 + I&5 + I&8 = 0ïï −I&5 + I&6 − I&9 = 0ïþ

(2.35)

Эта система уравнений выражает первый закон Кирхгофа для токов ветвей. Ее можно записать в матричной форме:

AI&B = 0

Обозначим теперь потенциалы узловых точек через ϕ&n (индекс n соответст-

вует номеру узла, в котором измеряется потенциал относительно базисного узла). Если умножить элементы матрицы А на потенциалы соответствующих узлов и за- тем просуммировать полученные произведения по столбцам, то можно видеть, что каждая такая сумма будет представлять собой напряжение ветви графа, равное разно- сти потенциалов в узлах этой ветви:

(2.38)

Эту систему можно записать в матричной форме:

ATϕ&у = U&B.

(2.39)

Умножим левую и правую части уравнения (2.24) на матрицу А и учтем соотношения (2.36) и (2.39), в результате получим

(AYB AT )ϕ&у = A(J& − YB Ė).

(2.40)

Тройное матричное произведение

называется матрицей узловых проводимостей. Здесь Υ11,Υ22,..., YPP – собствен-

ные проводимости узлов, представляющие собой сумму проводимостей всех ветвей, сходящихся k данному узлу; Ykl – взаимная проводимость, представляющая

собой проводимость ветви между узлами k и l, взятую с обратным знаком. Предпо- лагается, что цепь не содержит индуктивно связанных ветвей. Если проводи- мость ветви между узлами k и l будет YBkl, тο соответствующий элемент матри-

цы (2.41) Yk= – YBkl.

Пример 2.4. Составить матрицу узловых проводимостей для цепи, граф кото- рой показан на рис. 2.16.

Решение. Для заданного графа составим узловую матрицу:

Запишем произведение матрицы проводимостей ветвей ΥB и транспонированной узло- вой матрицы АT:

Подставим в уравнение (2.40) значение тройного матричного произведе- ния (2.41), произведём умножение матриц в левой и правой частях и запишем полученный результат в виде системы алгебраических уравнений:

представляет собой сумму токов от всех источников тока за вычетом суммы то-

Определив значения узловых потенциалов, можно найти напряжения на зажимах ветвей как разность соответствующих узловых потенциалов, а затем получить токи ветвей.

2.6.3. Уравнения переменных состояния

Вынесем за пределы анализируемой схемы независимые источники и ре- активные элементы. Оставшаяся часть схемы будет представлять собой линей- ную пассивную R-цепь, токи и напряжения в которой не изменят своих значений, если индуктивные элементы заменить источниками тока, а емкост- ные – источниками напряжения. В результате линейная часть схемы оказывается под воздействием источников двух типов: независимых источников, представляемых вектором

и источников замещения реактивных элементов

X = UC , IL

называемых вектором состояния.

При известных напряжениях и токах независимых источников напряжения и токи всех элементов схемы в любой момент времени определяются вектором состояния для этого момента времени. Поэтому метод

анализа схемы с описанием протекающих процессов с использованием вектора состояния называется методом переменных состояния. Согласно этому методу для анализа схемы необходимо составить два уравнения:

×

X (t) = A1X (t) + A2 Xни (t),

(2.42)

Xвых (t) = D1X (t) + D2 X ни (t),

(2.43)

×

где X (t) – производная вектора состояния по времени, X ни (t) – вектор независимых источников;

X вых (t) – вектор подлежащих расчету токов и напряжений; A1, A2, D1, D2 – матричные коэффициенты.

Уравнение (2.42) называют уравнением состояния, уравнение (2.43) – уравнением выхода. Для составления уравнения состояния необходимо выбрать дерево графа так, чтобы оно содержало все конденсаторы и источники ЭДС, но не содержало катушек индуктивности и источников тока. Такое дерево графа будем называть нормальным деревом. Сечением будем называть замкнутую линию, которая однократно пересекает ветви некоторой совокупности ветвей графа и разделяет граф на две несвязанные части. Если такая линия пересекает одно ребро, то будем называть ее главным сечением.

Матрица F, называемая матрицей главных сечений, определяет связь между токами ребер I р и токами хорд Ix : I р = − FIх .

С помощью транспонированной матрицы F можно выразить зависимость между напряжениями хорд Ux и напряжениями ребер U р : Ux = FTU р . Строки и столбцы матрицы F можно сгруппировать по типам элементов:

Матрицу главных сечений можно получить из узловой матрицы. Это осу- ществляется путем проведения последовательных операций исключения пере- менных узловой матрицы так, чтобы в левой части получилась единичная мат- рица. Матрица в правой части при этом будет представлять собой искомую мат- рицу главных сечений.

Пример 2.5. Получим матрицу главных сечений для схемы рис. 2.17.

Рис. 2.17. Принципиальная схема цепи Решение. Граф рассматриваемой схемы имеет вид, представленный на

рис. 2.18.

6

Рис. 2.18. Граф цепи

Узловая матрица для рассматриваемой схемы имеет вид

Получим матрицу главных сечений: