ИТиУвТС / ТЭС, вариант 19

Задача 1

1. Запишите формулы для расчета спектральных коэффициентов ряда Фурье в тригонометрической форме.

2. Вычислите спектральные коэффициенты для сигналов, приведенных на рис. 1. Интервал разложения равен [-τ/2; τ/2]. Число спектральных коэффициентов n = 5.

где

2. Вычисление спектральных коэффициентов сигнала

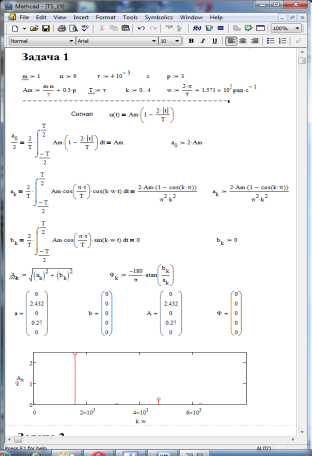
Запись ряда Фурье

Задача 2

Задача 3

1. Дайте определение автокорреляционной функции (АКФ) сигнала и за- пишите формулу для еѐ расчета.

2. Для заданного сигнала u(t) с параметрами определите АКФ одним из предложенных способов.

Автокорреляционная функция - это характеристика сигнала, которая помогает находить повторяющиеся участки сигнала или определять несущую частоту сигнала, скрытую из-за наложений шума и колебаний на других частотах. Автокорреляционная функция используется в обработке сигналов и анализе временных рядов.

Автокорреляционная функция - это сходство между значениями сигнала как функция от разницы во времени между ними.

Автокорреляционная функция - функция, характеризующая автокорреляционные свойства сигнала.

где τ – временной сдвиг.

Считается, что сигнал обладает хорошими автокорреляционными свойствами, если пик автокорреляционной функции максимальный, а уровень ее боковых лепестков минимален.

График автокорреляционной функции можно получить, отложив по оси ординат коэффициент корреляции двух функций (базовой и функции сдвинутой на величину ) а по оси абсцисс величину . Если исходная функция строго периодическая, то на графике автокорреляционной функции тоже будет строго периодическая функция. Таким образом из этого графика можно судить о периодичности базовой функции, а следовательно и о её частотных характеристиках. Это применяется для анализа сложных колебаний, например электроэнцефалограммы человека.

Автокорреляционная функция – четная функция поэтому

Значение АКФ про сдвиге τ = 0 равно энергии сигнала.

Вычисляем АКФ графическим способом.

Для упрощения расчетов сдвинем ось времени на τ/2

АКФ будет определяться площадью перекрытия импульсов

Задача 4

1. Приведите формулу для определения энергии.

2. Определите энергию сигнала u(t) с параметрами согласно варианта.

Энергия сигнала

Задача 5

Составьте структурную электрическую схему модулятора шумоподобного сигнала (ШПС). Опишите работу модулятора. В ячейках регистра сдвига генера- тора ШПС до подачи тактовых импульсов хранятся кодовые комбинации (табл.8,вариант 19). Электронный ключ модулятора подключен к ячейке регистра, номер которой со- ответствует номеру группы р потока.

Структурная схема модулятора

Г

1

0

1

0

0



Наиболее распространенный подкласс генераторов ШС строится на базе цифровых автоматов. Если формируемая на его выходе двоичная последовательность получена с использованием операций задержки и логической операции суммирования по модулю два, то такой автомат называется линейным, а формируемая на его выходе последовательность — линейной последовательностью. Если кроме указанных операций используются дополнительные логические операции (например, операция И), то формируемая цифровым автоматом двоичная последовательность называется нелинейной.

На рисунке приведена схема генератора ШПС, кодированного М-последовательностью. Буквой М принято обозначать разновидность линейных двоичных последовательностей. Генератор содержит регистр сдвига с обратными связями и сумматор по модулю два. Подключение входов сумматора к выходам определенных ячеек регистра определяет структуру М- последовательности.

Таблица работы генератора. Х1=Х3Х5, Xk=Xk-1

Такт	Х1	Х2	Х3	Х4	Х5
0	1	0	1	0	0
1	1	1	0	1	0
2	0	1	1	0	1
3	0	0	1	1	0
4	1	0	0	1	1
5	1	1	0	0	1
6	1	1	1	0	0
7	1	1	1	1	0
8	1	1	1	1	1

При поступлении первого тактового импульса происходит смешение данных Xk+1=Xk, в ячейку Х1 записывается величина Х3Х5.

С поступлением последующих тактовых импульсов процесс смены состояний ячеек продолжится. В результате на их выходах будет генерироваться ШС, кодированные циклически сдвинутыми М-последовательностями. Каждый из этих ШС состоит из единичных элементов — импульсов прямоугольной формы. Их ам­плитуда равна или не равна нулю в соответствии с символом {0,1} М-последовательности.

Период М-последовательности N=2^k-1=2⁵-1=31, где k – число используемых регистров.

Задача 6

Для заданного конечного числа выборочных значений сигнала и числа выбо- рочных значений импульсной характеристики линейного дискретного фильтра (табл. 9) найти: – коэффициенты дискретного преобразования Фурье; – коэффициенты передачи линейного дискретного фильтра; – z – преобразование выборочных значений на входе фильтра и на выходе фильтра; – z – преобразование выборочных значений импульсной характеристики.