Задача 4. Элементы математической логики и теории автоматов

Конечный автомат задан графом, определенным в задаче 1 контрольной работы № 1. Вершины графа отождествляются с состояниями автомата таким образом, что множество состояний Q = {q₁, q₂ ,…, q_n}. Переход автомата из одного состояния в другое осуществляется под воздействием множества входных сигналов X={x₁, x₂, x₃, x₄}. Переходы определяются законом отображения Г вершин графа, причем каждому переходу соответствует только одна из букв множества X. При задании графа эти буквы расставить произвольно.

Автомат позволяет вырабатывать выходные сигналы Y={y₁, y₂, y₃}:

y₁ – переход из состояния q_i в состояние q_i (петля);

y₂ – переход из состояния q_i в q_j при i<j;

y₃ – переход из состояния q_i в q_j при i>j.

Осуществить структурный синтез конечного автомата. Реализацию осуществить на элементах, указанных в табл. 1, в соответствии с номером варианта. Обязательной является минимизация реализуемых функций.

Таблица 1

№ варианта	1	2	3	4	5	6	7	8	9	10
Тип элементов	И НЕ	И ИЛИ НЕ	ИЛИ НЕ	И ИЛИ НЕ	И НЕ	ИЛИ НЕ	ИЛИ НЕ	И ИЛИ НЕ	И НЕ	ИЛИ НЕ
Тип триггера	RS	JK	T	RS	JK	D	RS	T	D	RS

Решение:

Множество вершин X = {x₁, x₂, x₃, x₄, x₅}.

Вершины графа отожествляются с состояниями автомата таким образом, что множество состояний Q = {q₁, q₂, q₃, q₄, q₅}. Переход автомата из одного состояния в другое осуществляется под воздействием множества входных сигналов X={x₁, x₂, x₃, x₄}. Автомат позволяет вырабатывать выходные сигналы Y={y₁, y₂, y₃}. Так как в графе нет петель, выходной сигнал y₁ будет отсутствовать.

На основании аналитического описания ориентированного графа из задания № 1 запишем закон отображения состояний автомата:

Гq₁ = { q₂(x₁/y₂), q₄(x₂/y₂)},

Гq₂ = {q₁(x₃/y₃), q₃(x₄/y₂)},

Гq₃ = {q₂(x₁/y₃), q₄(x₂/y₂)},

Гq₄ = {q₁(x₃/y₃), q₅(x₄/y₂), q₃(x₁/y₃)},

Гq₅ = {q₄(x₂/y₃)}.

Обобщенная таблица переходов и выходов соответствующего конечного автомата представлена в табл. 2.

Таблица 2

X	Q	q1	q2	q3	q4	q5
X1		q2/y2	─	q2/y3	q3/y3	─
X2		q4/y2	─	q4/y2	─	q4/y3
X3		─	q1/y3	─	q1/y3	─
X4		─	q3/y2	─	q5/y2	─

Осуществим структурный синтез автомата, заданного табл. 1. В качестве элементов памяти используем JK-триггеры, в качестве элементной базы используем логические элементы И-НЕ.

n = 4 p ≥ log₂ n = log₂ 4 = 2;

m = 2 e ≥ log₂ m = log₂ 2 = 1;

r = 5 z ≥ log₂ r = log₂ 5 = 3.

q	w	w1	w2	w3
q1		1	0	0	2
q2		0	0	1	2
q3		0	1	0	2
q4		0	0	0	3
q5		0	1	1	1

Приступаем к кодированию:

	v
y2	1	5
y3	0	5

х	u	u1	u2
x1		0	0	3
x2		0	1	3
x3		1	1	2
x4		1	0	2

На основании результатов кодирования строим обобщенную таблицу переходов и выходов структурного автомата (табл.3), заменяя состояния, входные и выходные переменные их кодами.

Таблица 3

u1u2	w1w2w3	100	001	010	000	011
00		001/1	─	001/0	010/0	─
01		000/1	─	000/1	─	000/0
11		─	100/0	─	100/0	─
10		─	010/1	─	011/1	─

Используя таблицу переходов JK-триггера и данные предыдущей таблицы, составим обобщенную таблицу функционирования структурного автомата (табл.4). Функции возбуждения трех триггеров обозначены через J₁K₁, J₂K₂, J₃K₃, соответственно.

Таблица 4

u1	u2	w1(t)	w2(t)	w3(t)	w1 (t+1)	w2 (t+1)	w3 (t+1)	v	J1	K1	J2	K2	J3	K3
0	0	1	0	0	0	0	1	1	*	1	0	*	1	*
0	1	1	0	0	0	0	0	1	*	1	0	*	0	*
1	1	1	0	0	*	*	*	*	*	*	*	*	*	*
1	0	1	0	0	*	*	*	*	*	*	*	*	*	*
0	0	0	0	1	*	*	*	*	*	*	*	*	*	*
0	1	0	0	1	*	*	*	*	*	*	*	*	*	*
1	1	0	0	1	1	0	0	0	1	*	0	*	*	1
1	0	0	0	1	0	1	0	1	0	*	1	*	*	1
0	0	0	1	0	0	0	1	0	0	*	*	1	1	*
0	1	0	1	0	0	0	0	1	0	*	*	1	0	*
1	1	0	1	0	*	*	*	*	*	*	*	*	*	*
1	0	0	1	0	*	*	*	*	*	*	*	*	*	*
0	0	0	0	0	0	1	0	0	0	*	1	*	0	*
0	1	0	0	0	*	*	*	*	*	*	*	*	*	*
1	1	0	0	0	1	0	0	0	1	*	0	*	0	*
1	0	0	0	0	0	1	1	1	0	*	1	*	1	*
0	0	0	1	1	*	*	*	*	*	*	*	*	*	*
0	1	0	1	1	0	0	0	0	0	*	*	1	*	1
1	1	0	1	1	*	*	*	*	*	*	*	*	*	*
1	0	0	1	1	*	*	*	*	*	*	*	*	*	*

По этой таблице запишем СДНФ выходных функций V и функций возбуждения триггеров J₁K₁, J₂K₂, J₃K₃, зависящих от набора переменных u₁, u₂, w₁(t), w₂(t), w₃(t). В результате получим систему логических функций для построения комбинационной части автомата:

.

.

.

.

.

.

.

Минимизируем функции согласно картам Карно:

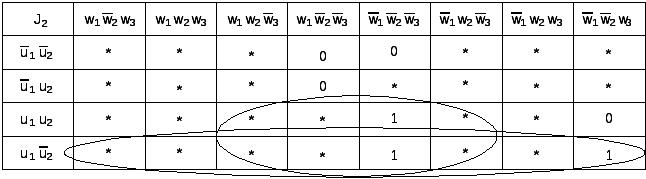
Представим логические функции в базисе И-НЕ:

; .

; .

; .

Функциональная схема структурного автомата: