
Сходимость метода
Теперь
докажем сходимость процесса итерации,
для этого надо доказать сходимость
![]() .
.
Выясним
условия сходимости последовательности
![]()
Теорема
1. Для того чтобы последовательность
приближений
![]() сходилась достаточно,
чтобы
все собственные значения матрицы B
были по модулю меньше единицы:
сходилась достаточно,
чтобы
все собственные значения матрицы B
были по модулю меньше единицы:
![]()
![]() . (3)
. (3)
Доказательство.
Найдем значение любого выражения
![]() через
через![]()
 (4)
(4)
Отсюда
и из условия теоремы с учетом свойств
опеделителя матрицы сразу следует что
при
![]()
![]() и
и
![]() ,
,
Откуда
![]() .
.
Теорема 2.
Если
требовать, чтобы последовательность
![]() сходилась к
сходилась к![]() при любом начальном приближении
при любом начальном приближении![]() ,
то условие (3) является необходимым
,
то условие (3) является необходимым
Доказательство.
Пусть для всякого начального приближения
![]() будет
будет![]() .
Имеем
.
Имеем
![]() .
.
При
![]() разность
разность![]() стремиться к нулю, поэтому последний
член цепи равенства должен стремиться
к нулю, каким бы ни был вектор
стремиться к нулю, поэтому последний
член цепи равенства должен стремиться
к нулю, каким бы ни был вектор![]() .
Отсюда следует, что
.
Отсюда следует, что![]() ,
последнее же будет лишь в том случае,
когда верно неравенство (3)
,
последнее же будет лишь в том случае,
когда верно неравенство (3)
Применение теорем 1 и 2 требует знания границ собственных значений матрицы В; нахождение их часто является нелегкой задачей. Укажем более простые, но только достаточные признаки сходимости.
Теорема 3.
Для
того чтобы последовательность приближений
![]() в методе простой итерации сходилась,
достаточно, чтобы какая-либо норма
матрицы В была меньше единицы.
в методе простой итерации сходилась,
достаточно, чтобы какая-либо норма
матрицы В была меньше единицы.
Доказательство.
Если
![]() ,
то все собственные значения матрицыВ
по
модулю меньше единицы, и по теореме 1
последовательность
,
то все собственные значения матрицыВ
по
модулю меньше единицы, и по теореме 1
последовательность
![]() сходится.
сходится.
Непосредственным следствием теоремы (3) и равенств определяющих кубическую и октаэдрическую норму матрицы, является
Теорема
4. Последовательность
![]() в методе простой итерации сходится,
если для матрицы В выполняется одно из
неравенств:
в методе простой итерации сходится,
если для матрицы В выполняется одно из
неравенств:
Для
многих приложений важно знать, какой
является скорость сходимости
![]() ,
и
уметь оценить Погрешность
,
и
уметь оценить Погрешность
![]() замены
точного решения
замены
точного решения![]() ситемы приближением
ситемы приближением![]() .
.
Теорема 5.
Если
какая-либо норма матрицы В, согласованная
с рассматриваемой нормой вектора
![]() ,
меньше единицы, то верна следующая
оценка погрешности приближения в методе
простой итерации:
,
меньше единицы, то верна следующая
оценка погрешности приближения в методе
простой итерации:
![]() . (5)
. (5)
Доказательство.
Для
![]() выше
дано выражение (4), и так как
выше
дано выражение (4), и так как![]() ,
то
,
то
![]()
Поэтому
![]() (6)
(6)
и, стало быть,
![]() .
.
Часто
за
![]() принимают векторb.
В этом случае оценка (5) немного упростится;
подставляя
принимают векторb.
В этом случае оценка (5) немного упростится;
подставляя
![]() =b
в (6) получим
=b
в (6) получим
![]() .
.
Метод Зейделя
Метод Зейделя применяют в двух видоизменениях. Рассмотрим сначала случай канонической формы системы для метода итерации
![]() (1)
(1)
В
методе простой итерации следующее
приближение
![]() находится по предыдущему
находится по предыдущему![]() путем подстановкиxk
в
правую часть всех уравнений системы
(1). Для нас сейчас удобнее записать
результат подстановки не в векторной
форме, а в развернутом виде по составляющим:
путем подстановкиxk
в
правую часть всех уравнений системы
(1). Для нас сейчас удобнее записать
результат подстановки не в векторной
форме, а в развернутом виде по составляющим:
 (2)
(2)
В этой операции порядок выбора уравнений значения не имеет. Здесь, очевидно; опускаются две возможности улучшения итераций: разумный выбор порядка уравнений для подстановок и немедленный ввод в вычисления каждого из полученных исправленных значений неизвестных.
О
принципах выбора порядка уравнений
будет говориться ниже, а сейчас
предположим, что для перехода от
приближения
![]() к
следующему —
к
следующему —![]() нами
выбран какой-то порядок привлечения
уравнений для подстановок. Изменяя,
если необходимо, нумерацию уравнений
и неизвестных, можно считать, что
уравнения для подстановок берутся в
порядке роста их номеров. Для каждого
шага от приближенияk
до
k+1
порядок
привлечения уравнений может быть своим,
и должны быть выполнены свои изменения
нумерации и перестановки, что влечет
за собой свое изменение матрицы В
системы
и свободного вектора b.
Чтобы
отметить это, обозначим матрицу В
для
рассматриваемого, шага
нами
выбран какой-то порядок привлечения
уравнений для подстановок. Изменяя,
если необходимо, нумерацию уравнений
и неизвестных, можно считать, что
уравнения для подстановок берутся в
порядке роста их номеров. Для каждого
шага от приближенияk
до
k+1
порядок
привлечения уравнений может быть своим,
и должны быть выполнены свои изменения
нумерации и перестановки, что влечет
за собой свое изменение матрицы В
системы
и свободного вектора b.
Чтобы
отметить это, обозначим матрицу В
для
рассматриваемого, шага
![]() и
свободный вектор
и
свободный вектор![]() .
В
этих обозначениях итерация в методе
Зейделя выполняется в следующем порядке:
.
В
этих обозначениях итерация в методе
Зейделя выполняется в следующем порядке:
 (3)
(3)
После
нахождения вектора![]() устанавливают
порядок подстановок в уравнения
значений
устанавливают
порядок подстановок в уравнения
значений
![]() (i
=
1, ..., п)
и
переходят к вычислению вектора
(i
=
1, ..., п)
и
переходят к вычислению вектора
![]() и т.д.
и т.д.
Приведем
теперь пример принципа, на основании
которого можно устанавливать порядок
привлечения уравнений для подстановок
![]() (i
=
1,...,п).
Можно
пытаться в первую очередь улучшить ту
составляющую решения, которая найдена
наименее точно, чтобы при нахождении
всех других составляющих употреблять
улучшенное ее значение. О точности
(i
=
1,...,п).
Можно
пытаться в первую очередь улучшить ту
составляющую решения, которая найдена
наименее точно, чтобы при нахождении
всех других составляющих употреблять
улучшенное ее значение. О точности
![]() можно
было бы судить по вектору погрешности,
можно
было бы судить по вектору погрешности,![]() ,
но так как вектор точного решения
,
но так как вектор точного решения![]() неизвестен,
то
неизвестен,
то![]() в вычислениях заменяют другим
вектором, по которому можно, хотя бы
неполно, судить о погрешности
в вычислениях заменяют другим
вектором, по которому можно, хотя бы
неполно, судить о погрешности![]() .
Чаще всего для этой цели пользуются
вектором поправки на последнем шаге
.
Чаще всего для этой цели пользуются
вектором поправки на последнем шаге![]() ,
где
,
где![]() .
Величины
поправок составляющих нумеруют в порядке
убывания их абсолютных значений, и в
том же порядке вычисляют составляющие
следующего приближения
.
Величины
поправок составляющих нумеруют в порядке
убывания их абсолютных значений, и в
том же порядке вычисляют составляющие
следующего приближения
![]() :
сначала ту составляющую, которая отвечает
наибольшей по модулю поправке, и т.д.
:
сначала ту составляющую, которая отвечает
наибольшей по модулю поправке, и т.д.
Пример:

Приведем эту систему к удобному для итерации
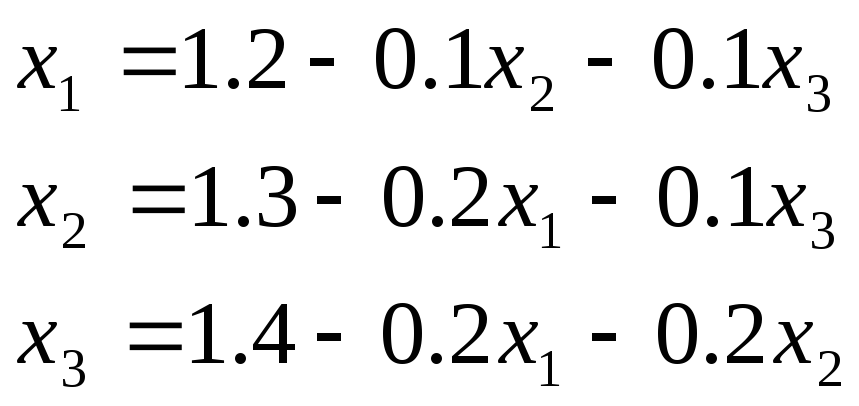
В
качестве нулевых приближений корней
возьмем
![]()
![]()
![]()
Применяя последовательно процесс решения методом Зейделя


Результаты вычисления корней приведены в Таблице 1ниже с точностью до 4-х знаков
|
i |
|
|
|
|
0 |
1.2000 |
0.0000 |
0.0000 |
|
1 |
1.2000 |
1.0600 |
0.9480 |
|
2 |
0.9992 |
1.0054 |
0.9991 |
|
3 |
0.9996 |
1.0001 |
1.0001 |
|
4 |
1.0000 |
1.0000 |
1.0000 |
|
5 |
1.0000 |
1.0000 |
1.0000 |
Таблица 1
Точные
значения:
![]() ;
;
![]() ;
;
![]()
