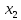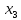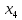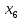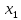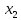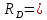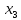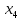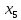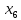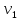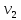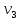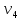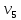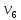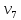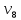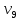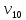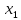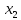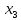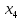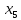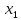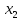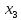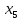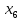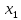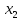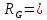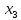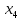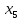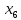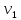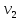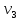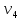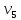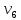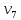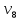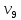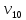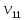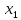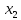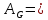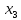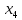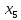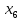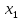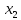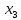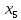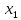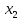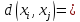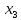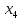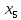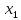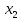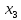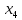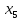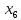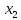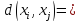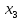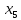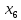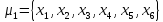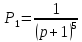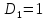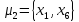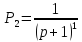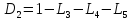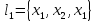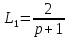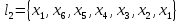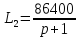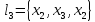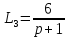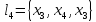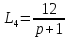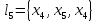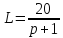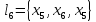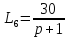Kursovaja_po_MOTS_19

^{ЗАДАНИЕ 1. ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ}

Связный ориентированный граф задан множеством 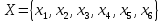и отображением Гx_i={x_|Ik|, x_I+l},

где i – текущий номер вершины,

n-количество вершин графа.

K=1; L=5; N=6;

Аналитический способ задания графа:

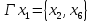
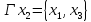
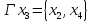
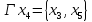
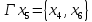
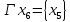
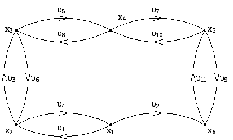
Графический способ задания графа:

- ориентированный граф:

-неориентированный граф:

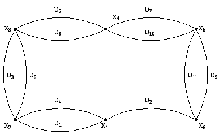
Матричный способ задания графа:

- ориентированный граф:

Матрица смежности:

			0	1	0	0	0	1
			1	0	1	0	0	0
			0	1	0	1	0	0
			0	0	1	0	1	0
			0	0	0	1	0	1
			0	0	0	0	1	0

Матрица инцидентности:

			1	1	0	-1	0	0	0	0	0	0	0
			-1	0	1	1	0	-1	0	0	0	0	0
			0	0	-1	0	1	1	0	-1	0	0	0
			0	0	0	0	-1	0	1	1	0	-1	0
			0	0	0	0	0	0	-1	0	1	1	-1
			0	-1	0	0	0	0	0	0	-1	0	1

- неориентированный граф:

Матрица смежности:

			0	2	0	0	0	1
			2	0	2	0	0	0
			0	2	0	2	0	0
			0	0	2	0	2	0
			0	0	0	2	0	2
			1	0	0	0	2	0

Матрица инцидентности:

			1	1	0	1	0	0	0	0	0	0	0
			1	0	1	1	0	1	0	0	0	0	0
			0	0	1	0	1	1	0	1	0	0	0
			0	0	0	0	1	0	1	1	0	1	0
			0	0	0	0	0	0	1	0	1	1	1
			0	1	0	0	0	0	0	0	1	0	1

Установим центры и периферийные вершины графов, найдем радиусы и диаметры графов.

Для ориентированного графа:

-матрица отклонений:

			0	1	2	3	2	1
			1	0	1	2	3	2
			2	1	0	1	2	3
			3	2	1	0	1	2
			4	3	2	1	0	1
			5	4	3	2	1	0

-вектор удаленностей:

В данном графе вершины x_1, x_2, x_3, x₄ являются центрами графа, вершины x₆ являются периферийными вершинами, соответственно радиус графа ρ(G) = 3; диаметр графа D(G) = 5

Для неориентированного графа:

-матрица отклонений:

			0	1	2	3	2	1
			1	0	1	2	3	2
			2	1	0	1	2	3
			3	2	1	0	1	2
			2	3	2	1	0	1
			1	2	3	2	1	0

-вектор удаленностей:

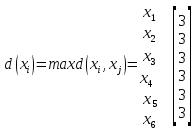
В данном графе все вершины являются центрами графа и периферийными вершинами, соответственно радиус графа ρ(G) = 3; диаметр графа D(G) = 3

Опишем систему уравнений, соответствующую сигнальному графу, считая, что передача между вершинами x_i и x_j:

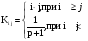
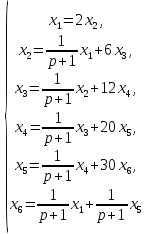
Сигнальный граф в соответствии с приведенной системой:

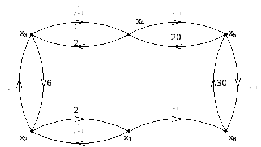
Найдем передачу между x₁ и x₆ по правилу Мезона.

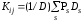
где: Р_s – передача S-го элементарного пути;

D – определитель графа, который зависит только от передач контуров;

D_s – алгебраическое дополнение для S-ro пути;

S – число элементарных путей.

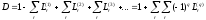
Элементарные пути из x₁ в x₆:

Контуры:

Пары несоприкасающихся контуров:

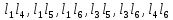
Тройки несоприкасающихся контуров:

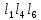
D = 1–(L₁+L₂+L₃+L₄+L₅+L₆)+L₁L₄+L₁L₅+L₁L₆+L₃L₅+L₄L₆+L₃L₆-L₁L₄L₆

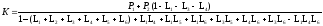
Приведем структурную схему системы, определяемой топологией графа

ЗАДАНИЕ 2. ЗАДАЧА О МАКСИМАЛЬНОМ ПОТОКЕ И ПОТОКЕ МИНИМАЛЬНОЙ СТОИМОСТИ

Транспортная сеть задана графом:

4

8

2/2

3/3

9/8

5/3

1/7

I

1

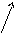
9/8

4/6

7