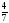ИТиУвТС / МОСТ Курсовая

Форматирование самостоятельно.

Работа выполнена в шаблоне. У всех одинаково. Для индивидуализации можешь исправить\заменить на синонимы\перефразировать описание, внести свои изменения. Преподша сказала, что ей важно решение, описание не надо, поэтому можно его и вовсе удалить, оставить для себя, чтоб знать, что сделано, и суметь ответить на вопросы на экзамене.

----------------------------------------------------

Задание 1: Линейное программирование.

1. Найти оптимальный план x* и экстремальное значение функции F(x).

2. Построить задачу, двойственную к исходной, решить её и сравнить решения прямой и двойственной задач.

3. Если решение не является целочисленным, получить целочисленное решение путём введения дополнительных ограничений по методу Гомори.

Вариант 5.

1) Условия задачи: F(x) = 3x₁ +3x₃ (min)

Для удобства заполнения симплекс-таблицы приведем ограничения к виду «≤», умножив обе части неравенства на «-1».

Приведем ограничения к виду равенств, введя дополнительные переменные со знаком «+», т.к. ограничения вида «≤»:

Матрицы A, Bи C^Tвыглядят следующим образом:

_A=; B= ; С^T =

Симплекс-таблица выглядит следующим образом:

БП	СЧ	НП
		x1	x2	x3
x4 x5 x6	-12 33 -30	3 3 -5	-4 2 -4	-3 6 -1
Fmin	0	3	0	3

Производится поиск базисного решения. Т.к. не все свободные члены положительны, значит, решение не является допустимым.

Производим пересчет симплекс-таблицы:

Определяем, какую небазисную переменную введем в базис, и какую базисную переменную выведем из базиса. Для этого выбираем любой из отрицательных элементов столбца свободных членов.

Пусть это будет b₃= -30 < 0.Просматриваем строку, в которой находится этот элемент, и выбираем любой отрицательный элемент.

Пусть это будет a₃₂ = -4 < 0.

Таким образом, ведущим элементом будет являться элемент a₃₂ = -4. Ведущая строка x₆, ведущий столбец – x₂. Из базиса исключается переменная x₆, в базис вводится переменная x₂.

Производим пересчет симплекс-таблицы.

Элементы новой таблицы помечаются штрихом и вычисляются следующим образом:

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

Новая симплекс-таблица выглядит следующим образом:

БП	СЧ	НП
		x1	x6	x3
x4 x5 x2	18 18	8	-1	-2
Fmin	0	3	0	3

Все элементы столбца свободных членов положительны, следовательно, допустимое базисное решение найдено.

Признаком оптимальности является неотрицательность переменных в F-строке. c₁, c₂, c₃ ≥ 0. Следовательно, решение является оптимальным.

Оптимальное решение найдено:

F_min = 0

Оптимальный план:

x₄ = 18

x₅ = 18

x₂ =

2) Условия задачи:

F(x) = 3x₁ +3x₃ (min)

Так как задача минимизации, то условия приводим к виду «≥»:

=>

Матрицы A^T, Bи C выглядят следующим образом:

A^T= ; B = ; С =;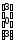

Количество переменных в двойственной задаче равно количеству переменных в прямой, и наоборот.

Тогда A^TY ≤ C примет вид:

Функция цели F(y) = B^TY = = 12y₁ -33 y₂ +30y₃ (max)

Так как среди ограничений прямой задачи нет равенств и на все переменные наложено условие неотрицательности, то двойственная задача симметрична.

Далее решение производится симплекс-методом.

Вводим дополнительные переменные и приводим ограничения к виду равенств.

БП	СЧ	НП
		y1	y2	y3
y4 y5 y6	3 0 3	-3 4 3	-3 -2 -6	5 4 1
Fmax	0	-12	33	-30

Базисное решение найдено. Производим поиск оптимального решения. Ведущей строкой будет та, которой соответствует максимальное абсолютное значение элемента c_l. В данной задаче это элемент c₃ = -30 < 0.

Ведущая строка определяется положительным минимальным симплексным отношением. В данной задаче оно достигается в строке, соответствующей элементу y₅. Таким образом, ведущий элемент a₂₃ = 4.

Производим пересчет симплекс-таблицы.

БП	СЧ	НП
		y1	y2	y5
y4 y3 y6	3 0 3	-8 1 2
Fmax	0	18	18

Элемент b₂ = 0. Решение является вырожденным. Дальнейшее преобразование невозможно.

Оптимальный результат:

F_max = 0

Оптимальный план:

y₄ = 3

y₃ = 0

y₆ = 3

Решения прямой и двойственной задачи совпадают.

3. Решение задачи без условия целочисленности приведено в пункте 1.

Задача имеет целочисленное решение, а значит и выполнение данного пункта не целесообразно.

Задание 2: Нелинейное программирование.

1. Построить область допустимых значений переменных.

2. Найти максимальное значение функции F(x) без учета ограничений на переменные, используя:

а) метод наискорейшего спуска

б) метод Ньютона

Процесс оптимизации начинать с точки x⁰.

3. Найти максимальное значение функции F(x) с учетом системы ограничений задачи, используя:

а) метод допустимых направлений Зойтендейка

б) условия теоремы Куна-Таккера

Процесс оптимизации начинать с точки x⁰.

Вариант 5.

F(x) = -5-2+4

x_1,2≥ 0

x⁰ = [4;1]

x1	2
x2	5	0

1) x₂ ≤

x1		2
x2	0	5

x₂ ≤

2)

а) Находим составляющие вектора градиента функции:

1 шаг: Движение осуществляется из x⁰вдоль в новую точку x¹:

Градиент в точке x⁰ равен:

Координаты точки x¹определяются выражением:

Величину шага определим из условия:

В результате точка x¹:

2 шаг:

Градиент в точке x¹равен:

Координаты точки x² определяются выражением:

Величину шага определим из условия:

В результате точка x²:

3 шаг:

Градиент в точке x²равен:

Координаты точки x³ определяются выражением:

Величину шага определим из условия:

В результате точка x³:

В точке х³ функция достигает значения

_Fmax =

Метод наискорейшего спуска неэффективен при приближении к точке экстремума, поэтому существует погрешность.

б) Так как функция цели квадратичная, экстремум будет найден за один шаг.

H^-1= , где detH– определитель матрицы H.

detH = (-10)∙(-4) –0∙0 = 40 – 0 = 40.

AdjH – присоединенная к H матрица (транспонированная матрица алгебраических дополнений).

Найдем алгебраические дополнения элементов матрицы H:

, тогда:

Тогда AdjH=; H^-1 = ;

_Fmax =

Равенство градиента нулю показывает, что найденная точка является экстремальной, а решение – оптимальным. Исходя из этого, можно построить графики функций и наглядно увидеть, что метод наискорейшего спуска оставляет погрешность и эффективен только для задач с большим удалением начальной точки от точки максимума, а метод Ньютона позволяет за один шаг определить экстремум квадратичной функции.

3) а)

Градиент в точке х⁰ равен:

Выбираем наиболее сильные условия:

Находим значение как в методе наискорейшего спуска. . Данное значение не принадлежит найденному интервалу, поэтому .

Таким образом, точка попадает на ограничение .

Точка х¹ равна:

Градиент в точке х¹ равен:

Движение в этом направлении выводит за пределы ОДЗП, поэтому очередная точка поиска будет производиться в направлении S¹:

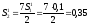
Выбираем наиболее сильные условия:

-2,51 ≤ ≤ 11,78

Определяем значение при котором функция будет достигать максимальной величины. Для этого подставляем в исходную функцию:

Данное значение находится вне допустимого интервала.

Принимаем значение

Точка лежит на ограничениях и .

Градиент в точке x² равен:

_{Градиент направлен в противоположную сторону от области допустимых значений переменных, а это значит, что данная точка является оптимальной.}

Функция достигает максимума в точке .

F_max = 0,64.

б) Составим функцию Лагранжа:

Запишем условия теоремы Куна-Таккера: Производные и, так как цель максимизация.

БП	СЧ	НП
		x1	x2	λ1	λ2
v1 v2 w1 w2	-4 0 -4 16	-10 0 -7 3	0 -4 2 2	7 -2 0 0	-3 -2 0 0

БП	СЧ	НП
		v1	x2	λ1	λ2
x1 v2 w1 w2	0	0	0 -4 2 2	-2	-2

БП	СЧ	НП
		v1	x2	w1	λ2
x1 v2 λ 1 w2		0 0			0 0

Решение, определяемое последней таблицей, соответствует допустимому базисному решению x₁ = ; v₂ = ; λ₁ = ; w₂ = ; v₁ = x₂ = w₁ = λ₂ = 0.

Выполняется условие x₁∙ v₁ = x₂∙ v₂ = λ₁∙ w₁ = λ₂∙ w₂ = 0, поэтому является оптимальным решением задачи.

При этом F_max= 0,64.