Занятие 6. Контрольная работа №1. Прием части-1 бдз.

☺ ☻ ☺

Контрольная работа №1 предназначена оценить степень усвоения основных терминов, определений и свойств геометрических фигур, изучаемых «Аналитической геометрии».

Состав и степень трудности предлагаемых в Контрольной работе заданий согласовывается с Методическим советом кафедры «Высшая математика».

При разработке заданий Контрольной работы учитывается также требование побудить студентов повторить пройденный материал по предмету. Это значит, что в заданиях не должно быть ничего такого, что, так или иначе, требует самостоятельных обобщений и выводов со стороны студентов.

Перед выполнением Контрольной работы студенты должны ознакомиться с перечнем вопросов, которые будут отражены в заданиях. Так же важным элементом подготовки к контрольной работе должны быть регулярные текущие контрольные мероприятия в виде оперативных опросов: по 6-7 минут в начале каждого занятия.

Прием части-1 БДЗ. Приём БДЗ определяется двумя последовательными мероприятиями:

1). Формальный приём выполненных Заданий непосредственно в аудитории: проверка на соответствие правилам закрепления вариантов заданий за каждым студентом.

2). Контроль выполненных Заданий преподавателем: проверка правильности решения заданий и соответствия требованиям по оформлению каждого задания БДЗ.

3). Защита выполненных заданий БДЗ каждым студентом в специально назначенное время (обычно, в день консультаций по предмету). Определение окончательной оценки качества выполнения Части-1 БДЗ.

Замечание: 1). Сборник заданий по БДЗ находится в информационной системе института с самого начала семестра, постоянно.

2). Сборник заданий по БДЗ содержит по каждому заданию примеры решения и оформления.

< * * * * * >

Занятие 7. Кривые второго порядка: окружность, эллипс, гипербола, парабола. Общие свойства кривых второго порядка.

☺ ☻ ☺

Окружность: основные определения и формулы:

Если точка – произвольная точка плоскости, а точка – фиксированная точка, то = – векторная форма записи окружности, в координатной форме уравнение окружности имеет вид:

→ нормальное уравнение. (1)

Если центр окружности находится в начале координат (0,0), то уравнение (1) принимает простейший вид: → каноническое уравнение. (2)

Если вместо выражения (1) имеем равенство: , то нетрудно получить выражение: . (3)

В зависимости от величины Е могут реализоваться такие случаи:

1). > 0 , то есть → окружность: .

2). = 0 → , выполняется для одной точки (x₀,y₀) .

3). < 0 , то есть → – мнимая окружность.

••• ≡ •••

Пример 1–242: Пусть – центр окружности, – радиус окружности, , , , – точки окружности. Составить уравнение окружности в каждом из следующих случаев:

1) (2,–3), =7; 2) (2,6), (–1,2); 3) (3,2), (–1,6) – концы диаметра окружности; 4) (1,–1), прямая линия : =0 касается окружности; 5) (1,2) – точка окружности, окружность касается координатных осей; 6) (3,1), (–1,3) – точки окружности, принадлежит прямой : =0; 7) (–1,3), (0,2), (1,–1) – точки окружности.

Решение:

1). Сразу записываем уравнение окружности: .

2). Из условия имеем: = =(2,6)–(–1,2)=(3,4) → = =5. Тогда уравнение окружности: .

3). Так как центр окружности делит заданный отрезок пополам, то = , откуда: 2 = + =(2,8) → =(1,4). В то же время = =(–4,–4) → =2 . Тогда уравнение окружности: .

4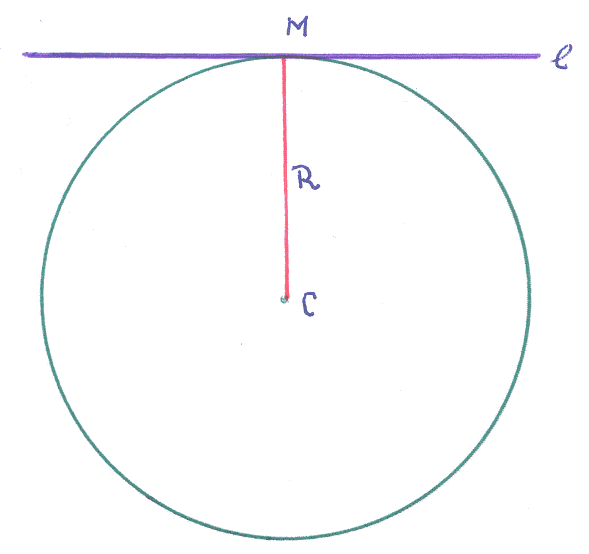 ). Радиус окружности равен расстоянию до касательной. Нормируем уравнение прямой линии и находим отклонение точки от этой прямой: = =2 → =2. Тогда – уравнение окружности.

5). Обозначим радиус окружности = . Учитывая свойство касания окружности осей координат, запишем уравнение окружности: . Так как точка принадлежит окружности, то необходимо: . Из уравнения получаем два корня: =1 и =5. Решение: или .

6). Точки (3,1) и (–1,3) выделяют на окружности хорду . Известна теорема, что прямая линия , проходящая через середину хорды окружности и ей перпендикулярная, проходит через центр этой окружности.

Н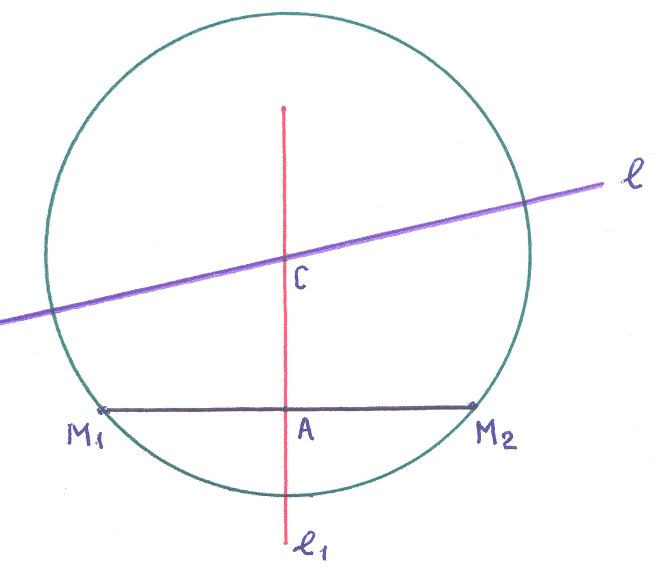 айдём уравнение . Из равенства 2 = находим (1,2). Запишем =(–2,1)= . Тогда уравнение : , или .

Точку пересечения прямых линий и найдём из системы уравнений: находим координаты центра (2,4). Радиус окружности: = = = . Тогда: – уравнение искомой окружности.

7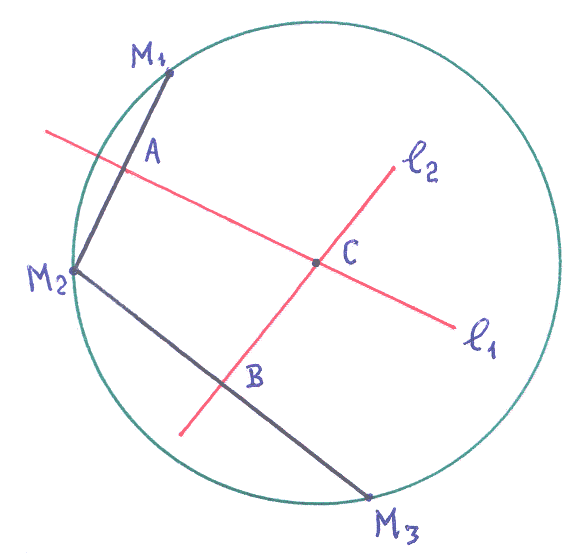 ). Найдём уравнение . Из равенства 2 = находим . Запишем = , примем =(3,–1). Тогда уравнение : , или .

Найдём уравнение . Из равенства векторов = имеем 2 = , находим . Запишем = , примем =(1,–3). Тогда уравнение : , или .

Точку пересечения прямых линий и найдём из системы уравнений: → (–4,–1). Радиус окружности: = = =5. Тогда: – уравнение искомой окружности.

Ответ: 1) , 2) , 3) ,

4) , 5) , 6) ,

7) .

☺ ☻ ☺

Эллипс: геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Если принять, что – большая полуось, то фокусы эллипса располагаются на оси , причём: = – левый фокус, = – правый фокус.

Каноническое уравнение эллипса имеет вид: , – большая полуось, – малая полуось. Величины , , связаны соотношением: = – .

В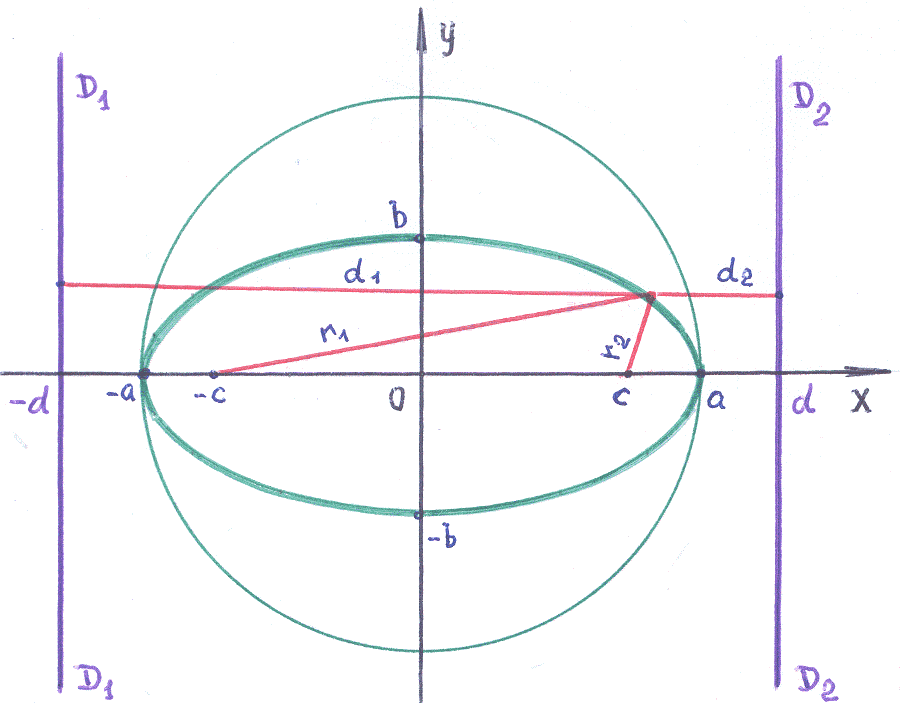 ажной характеристикой эллипса является величина: – эксцентриситет, которая определяет степень сжатия окружности вдоль оси .

Для вычисления расстояний до фокусов используют выражения: = , = , причём + =2 .

Особое место в свойствах эллипса занимают прямые линии: и – директрисы. Положение директрис определяет число: .

••• ≡ •••

Пример 2–246: Задано уравнение линии второго порядка: . Показать, что линия есть эллипс, записать его каноническое уравнение. Найти: а) полуоси, б) координаты фокусов, в) эксцентриситет, г) уравнения директрис.

Решение:

1). Перепишем уравнение: – это каноническое уравнение эллипса с фокусами, расположенными на оси .

2). Полуоси эллипса: =5, =3. Вычислим: = – =16. Это значит: = – левый фокус, = – правый фокус. Вычислим эксцентриситет: = = . Вычислим параметр директрисы: = = . Уравнения директрис : =– , : = .

Ответ: а) уравнение эллипса , =5, =3; б) фокусы = , = ; в) эксцентриситет = ; г) директрисы : =– , : = .

Пример 3–252: Главные оси эллипса совпадают с осями координат. Точки и (0,2) принадлежат эллипсу. Написать уравнение эллипса, найти фокальные радиусы точки и расстояние этой точки до директрис.

Решение:

1). Воспользуемся уравнением: . Обозначив (для удобства!): = и = , для точек и запишем систему: откуда = и = . Можем записать уравнение эллипса: . Причём, = – =12 и тогда запишем = .

2). Вычислим фокальные радиусы для точки , принадлежащей эллипсу: именно = = . = .

3). По определению директрисы, расстояние точки до левой директрисы вычисляем как = = , а до правой как = = .

Ответ: уравнение эллипса , фокальные радиусы = , = ; расстояния до директрисы : = , до директрисы : = .

Пример 4–254: Написать уравнение кривой, по которой движется точка , если сумма расстояний от неё до точек (–1,–1) и (1,1) остаётся постоянной и равна .

Решение:

1). Расстояние от точки до точки определяется выражением: = , а до точки выражением: = . По условию : = .

2). Выполнив тождественные преобразования выражения , окончательно запишем уравнение кривой линии, по которой движется точка , именно : .

Ответ: уравнение кривой линии : .

☺ ☻ ☺

Г ипербола: геометрическое место точек плоскости, для каждой из которых абсолютное значение разности расстояний до двух данных точек плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами:

Пусть фокусы гиперболы располагаются на оси , причём: = – левый фокус, = – правый фокус. Каноническое уравнение гиперболы имеет вид: , причём < и . Эксцентриситет гиперболы: . Фокальные расстояния определяются выражениями:

– левая ветвь → ( – ) =–2 .

– правая ветвь → ( – ) =2 .

Директрисы гиперболы и определяются параметром . Асимптоты гиперболы определяют выражения: = ± .

Замечание: для принятого расположения фокусов ось называют действительной осью гиперболы, ось – мнимой осью.

••• ≡ •••

Пример 5–265: Задано уравнение линии второго порядка: . Показать, что линия есть гипербола, записать её каноническое уравнение. Найти: а) полуоси, б) координаты фокусов, в) эксцентриситет, г) уравнения директрис и асимптот.

Решение:

1). Перепишем уравнение: – это каноническое уравнение гиперболы с фокусами, расположенными на оси .

2). Полуоси гиперболы: =3, =4. Вычислим: = + =25. Это значит: = – левый фокус, = – правый фокус. Вычислим эксцентриситет: = = . Вычислим параметр директрисы: = = . Уравнения директрис : =– , : = . Уравнения асимптот выражением: = ± = ± .

Ответ: а) уравнение гиперболы , =3, =4; б) фокусы = , = ; в) эксцентриситет = ; г) директрисы : =– , : = , асимптоты: = ± .

Пример 6–269: Задано уравнение линии второго порядка. Показать, что линия есть гипербола, найти её центр и записать её каноническое уравнение. Найти: а) полуоси, б) координаты фокусов, в) эксцентриситет, г) уравнения директрис и асимптот.

Решение:

1). Перепишем уравнение: – это каноническое уравнение гиперболы с фокусами, расположенными на прямой линии =3, с центром в точке (2,–3).

2). Воспользуемся параллельным переносом системы координат: , . Тогда уравнение принимает канонический вид, для которого все величины можно переписать из Примера 5-265. Полуоси гиперболы: =3, =4. Вычислим: = + =25. Это значит: = – левый фокус, = – правый фокус. Вычислим эксцентриситет: = = . Вычислим параметр директрисы: = = . Уравнения директрис : =– , : = . Уравнения асимптот выражением: = ± = ± .

3). Учитывая , , запишем уравнения для старой системы координат: для директрис : = , : = и для асимптот +3 = ± . Фокусы: = , = .

Ответ: а) уравнение гиперболы , =3, =4; б) фокусы = , = ; в) эксцентриситет = ; г) директрисы : = , : = , асимптоты: +3 = ± .

☺ ☻ ☺

Парабола: геометрическое место точек плоскости, для каждой из которых расстояние до данной точки плоскости, называемой фокусом, равно расстоянию до данной прямой, называемой директрисой.

В соответствии с определением параболы, отметим на плоскости точку – фокус и прямую : = – директрису:

И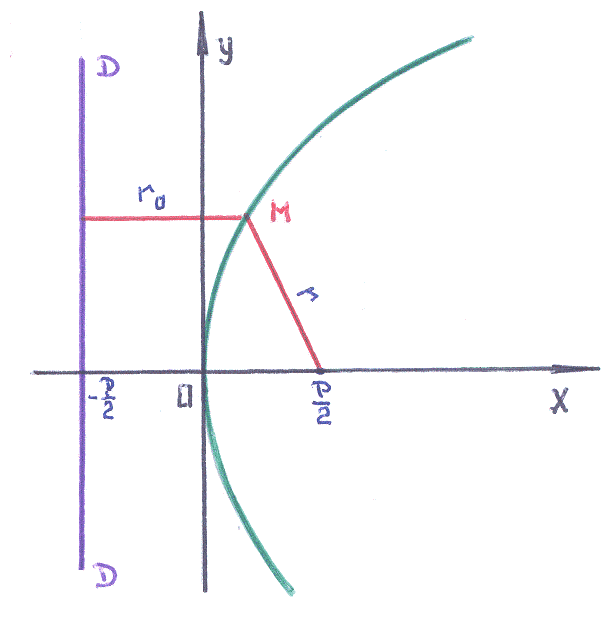 спользуя принятые на рисунке обозначения, в соответствии принятым определением параболы , легко получают каноническое уравнение параболы . (17)

Для параболы имеем: – эксцентриситет.

Замечание: рисунок и расположение директрисы и фокуса соответствуют случаю, когда и осью параболы является ось .

••• ≡ •••

Пример 7–285: Построить параболы: 1) ; 2) ; 3) ; 4) . Найти параметр для каждой параболы.

Решение:

1). Перепишем уравнение: . Имеем параболу с параметром =2, причём график заданной параболы – это график параболы , смещённый вправо на 2.

2). Из уравнения: следует, что осью параболы является ось . Имеем параболу с параметром = , ветви параболы направлены вверх.

3). Из уравнения: следует, что осью параболы является ось . Имеем параболу с параметром =–2, причём график заданной параболы – это график параболы , симметрично отображённый относительно оси .

4). Из уравнения: следует, что осью параболы является ось . Имеем параболу с параметром =– , причём график заданной параболы – это график параболы , симметрично отображённый относительно оси .

•◄ Дополнительно ►•

Пример 8–274. Записать уравнение гиперболы, если известно, что её фокусами являются точки =(–3,–4) и =(3,4), а расстояние между директрисами равно 3,6.

Р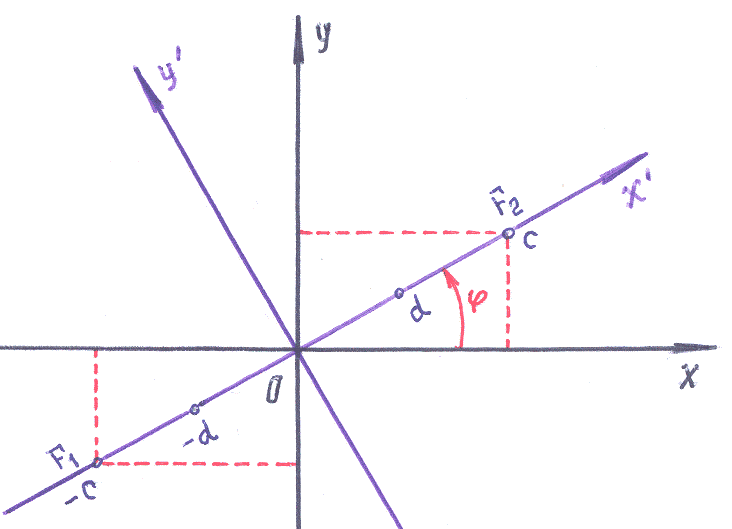 ешение:

1). Легко заметить, что точки и расположены симметрично относительно начала координат и расстояние между ними равно 10. Так как известно, что заданная кривая есть гипербола, то воспользуемся системой координат , в которой фокусы и гиперболы располагаются на оси и имеют координаты: (–5,0) и (5,0).

2). Так как параметр директрисы = = , то из условия: = запишем =9. Теперь можем вычислить: = – =16 и записать каноническое уравнение гиперболы в системе координат : .

3). Система координат получена из системы координат поворотом относительно точки на угол , такой что: = и = . Воспользуемся формулами перехода: → (S)

Подставляя (S) в каноническое уравнение гиперболы: достаточно просто получаем уравнение заданной гиперболы в координатах : .

Ответ: уравнение гиперболы: .

Пример 9–293. Записать уравнение касательной к параболе , параллельной прямой линии: .

Решение:

1). Перепишем уравнение касательной: . Отсюда получаем угловой коэффициент касательной: =–1.

Замечание: можно было бы воспользоваться универсальными средствами математического анализа и выделить на параболе точку, в которой .

2). Воспользуемся готовым уравнением касательной к параболе в точке , именно: → .

3). В нашем случае =4. Тогда для точки получаем: =–1. Из равенства: получаем =2. Можем записать уравнение касательной: .

Ответ: уравнение касательной: .

☻

Вопросы для самопроверки:

1. Что такое окружность, эллипс?

2. Что такое гипербола?

3. Что такое парабола?

4. Что такое эксцентриситет кривой второго порядка?

5. Что такое директриса для кривой 2-го порядка?

< * * * * * >

Задачи для самоподготовки:

Пример C7–1: Написать уравнение диаметра окружности: , перпендикулярного прямой линии : .

Ответ: уравнение диаметра : .

Пример C7–2: Написать каноническое уравнение эллипса, если известно, что: 1) =3, =2; 2) =5, =4; 3) =3, = ; 4) =5, = ; 5) =2, 2 =5; 6) = , 2 =32.

Ответ: для случаев: 1) , 2) , 3) , 4) .

5) , 6) .

Пример C7–3: На эллипсе: найти точку, расстояние которой до фокуса в 4 раза больше расстояния до фокуса .

Ответ: точка: .

Пример C7–4: Написать уравнение кривой, по которой движется точка , если расстояние её до точки (3,0) остаётся в 2 раза меньше расстояния до прямой линии : .

Ответ: уравнение кривой линии : .

Пример C7–5: Задано уравнение линии второго порядка: . Показать, что линия есть гипербола, записать её каноническое уравнение. Найти: а) полуоси, б) координаты фокусов, в) эксцентриситет, г) уравнения директрис и асимптот.

Ответ: а) уравнение гиперболы , =4, =3; б) фокусы = , = ; в) эксцентриситет = ; г) директрисы : =– , : = , асимптоты: = ± .

Пример C7–6: Задано уравнение линии второго порядка. Показать, что линия есть гипербола, найти её центр и записать её каноническое уравнение. Найти: а) полуоси, б) координаты фокусов, в) эксцентриситет, г) уравнения директрис и асимптот.

Ответ: а) уравнение гиперболы , =8, =6; б) фокусы = , = ; в) эксцентриситет = ; г) директрисы : =– , : = , асимптоты: –1 = ± .

Пример C7–7: Написать уравнение параболы с вершиной в начале координат, если известно, что: 1) парабола расположена в левой полуплоскости симметрично оси и = ; 2) парабола расположена симметрично оси и проходит через точку (4,–8); 3) фокус параболы расположен в точке (0,–3).

Ответ: параболы: 1) , 2) , 2) .

< * * * * * >