Занятие 2. Определители 2-го порядка и системы линейных уравнений с двумя неизвестными. Определители 3-го порядка. Простейшие правила вычисления определителей.
☺ ☻ ☺
Определители 2-го и 3-го порядков появились в связи с решением систем линейных уравнений 2-го и 3-го порядков. Этот факт мы будем наблюдать при изучении определителей произвольного порядка. В настоящем параграфе рассматриваются только формальные правила вычисления определителей 2-го и 3-го порядков: этого будет достаточно при изучении векторного произведения двух векторов, а также в некоторых геометрических задачах на плоскости и в пространстве.
Определители 2-го порядка.
Определителем
2-го порядка называют число,
представленное в виде специальной
записи: 
=
=
. (1)
Говорят, что правая часть выражения (1) определяет правило вычисления определителя 2-го порядка. При использовании определителя применяют термины:
▫ элементы определителя – числа a11, a12, a21, a22;
▫ строки определителя: 1-я строка: пара чисел: a11,a12 , 2-я строка: пара чисел a21,a22;
▫ столбцы определителя: 1-й столбец: пара чисел: a11,a21, 2-й столбец: пара чисел a12,a22;
▫ члены определителя: (a11·a22) и (–a21·a12).
При внимательном рассмотрении соответствия (1) нетрудно заметить правило использования элементов определителя для записи суммы левой части выражения (1). Для записи положительного члена определителя (a11·a22) используют схему:
Для записи отрицательного члена определителя (–a21·a12) используют схему:
Рассмотрим несколько примеров вычисления определителей 2-го порядка, использующих в качестве своих элементов числа, или некоторые аналитические выражения.
Пример 2–1:
Вычислить
определитель 2-го порядка:
=
.
Решение:
1). Воспользуемся общей формулой: = = .
2). В нашем примере: d=(-1)·2–(-5)·4 = 18.
Ответ: =18.
Пример 2–6:
Вычислить
определитель 2-го порядка:
=
.
Решение:
1). Воспользуемся общей формулой: = = .
2). Прежде, чем вычислять определитель, воспользуемся формулами тригонометрии:
=
,
=
,
=
.
2).
Перепишем определитель с учётом
записанных формул:
=
,
после чего очевиден ответ:
=1.
Ответ: =1.
Пример
3–8: Решить
уравнение:
=
.
Решение:
1). Воспользуемся общей формулой вычисления: = = .
2). Вынося
общий множитель второго столбца за знак
определителя, получим:
=
=
·
.
3). Из
условия:
=0
получаем корни уравнения
=–1,
=–4.
Ответ: корни уравнения =–1, =–4.
Замечание: формальное применение правила вычисления определителей 2-го порядка не вызывает никаких затруднений!
Определители 3-го порядка.
Определителем 3-го порядка называют число, представленное в виде специальной записи:
=
=
+
+
–
–
–
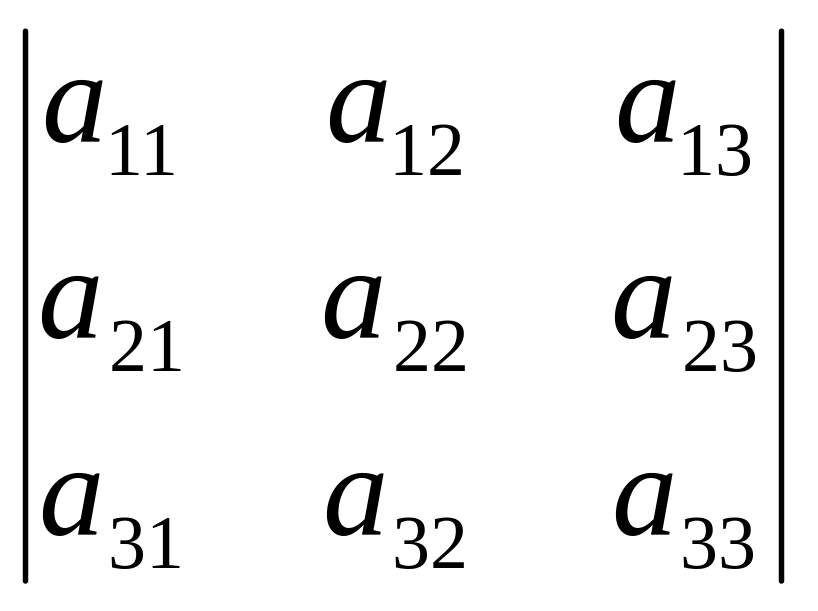. (2)
Говорят, что правая часть выражения (2) определяет правило вычисления определителя 3-го порядка. Соответствие, представленное выражением (2), легко запоминается, если использовать геометрическую схему составления членов определителя:
Замечание: нетрудно заметить, что правило (1) вычисления определителя 2-го порядка запомнить значительно проще, чем правило (2) для определителей 3-го порядка!
Оказывается, есть правило сведения вычисления определителя 3-го порядка к вычислению нескольких определителей 2-го порядка, а именно:
=
=
–
+
, (3)
или
=
=
–
+
, (4)
Обоснование
правил (3) и (4) вычисления определителя
3-го порядка мы получим в теории
определителей
-
го порядка.
Замечание: правило (3) называют: вычисление определителя разложением по первой строке, а правило (4): разложение по первому столбцу.
Рассмотрим несколько примеров вычисления определителей 3-го порядка, использующих в качестве своих элементов числа, или некоторые аналитические выражения.
Пример 4–12:
Вычислить
определитель 3-го порядка:
=
.
Решение:
Вычислим
определитель, применяя правило (2) и
учитывая принятые обозначения:
=
,
или:
=
=0.
Ответ: d = 0.
Пример 5–15:
Вычислить
определитель 3-го порядка:
=
.
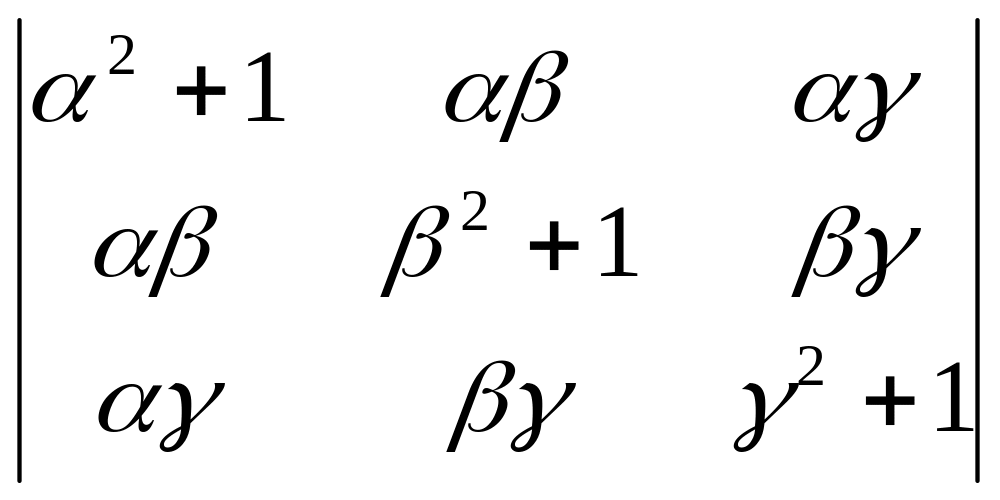Решение:
1). Воспользуемся формулой (3) вычисления:
=
–
+
,
или
=
–
+
.
2).
Применяя тождественные преобразования,
получаем величину:
=
.
Ответ: d = .
Пример
6–17: Вычислить
определитель 3-го порядка:
=
,
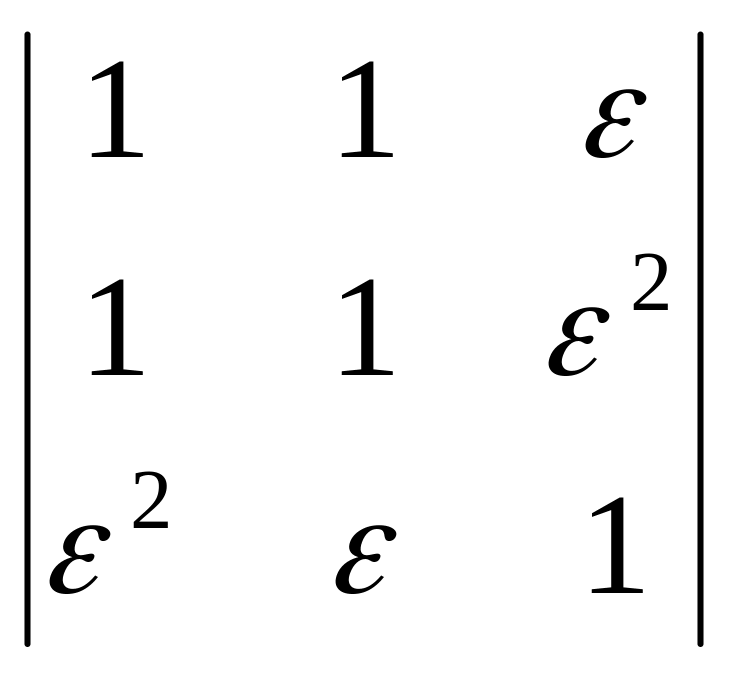учитывая, что
=
.
Решение:
1).
Воспользуемся формулой (3) вычисления:
=
–
+
,
или
=
–
+
=
.
2).
Запишем:
=
и
=
.
Тогда
=–3
(учтено:
=–1).
Ответ: d = –3.
☻
Вопросы для самопроверки:
1. Что такое определитель 2-го порядка, как его вычисляют?
2. Что такое определитель 3-го порядка, как его вычисляют?
Задачи для самоподготовки:
Пример
C2–1:
Вычислить
определитель:
=
.
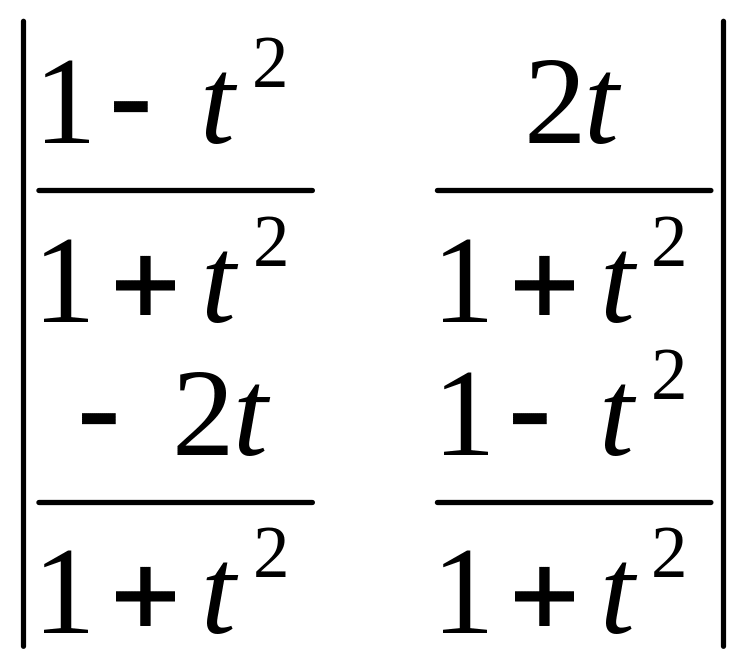Ответ: d =1.
Пример
C2–2:
Решить уравнение:
=
.
Ответ:
решение:
=
,
.
Пример
C2–3:
Вычислить
определитель:
=
.
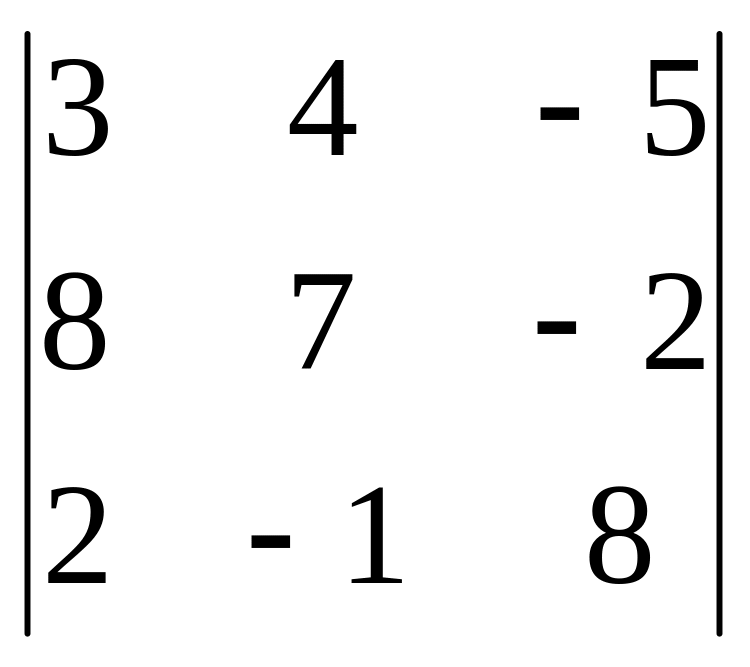Ответ: d =1.
Пример
C2–4:
Вычислить
определитель:
=
.
Ответ:
d
=
.
Пример
C2–5:
Вычислить определитель:
=
,
=
.
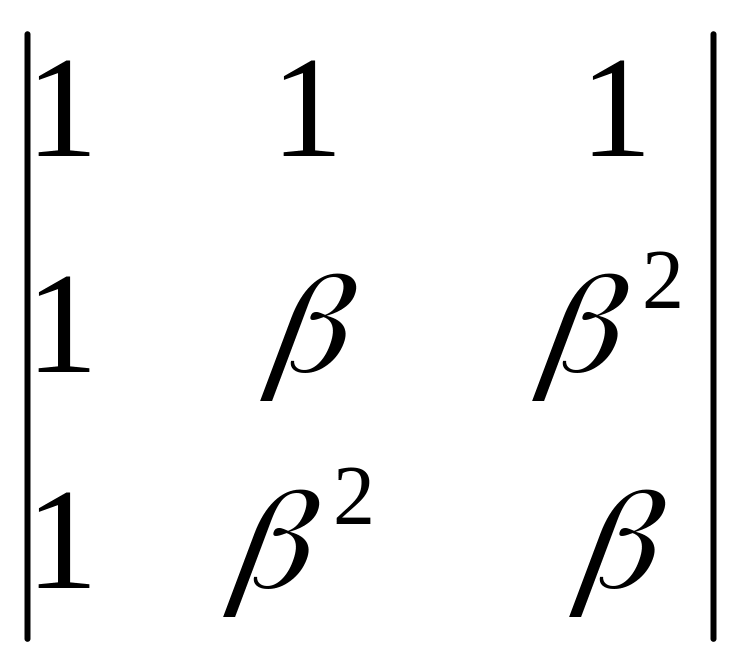Ответ:
d =
.
< * * * * * >
ЗАНЯТИЕ 3. Правые и левые тройки векторов. Векторное произведение векторов: определение и свойства (физический смысл). Векторное произведение векторов, заданных своими проекциями. Смешанное произведение векторов.
☺ ☻ ☺
Пусть
векторы
,
,
образуют правую тройку. Векторное
произведение для векторов
,
записывают в виде:
=
x
=
=
∙
–
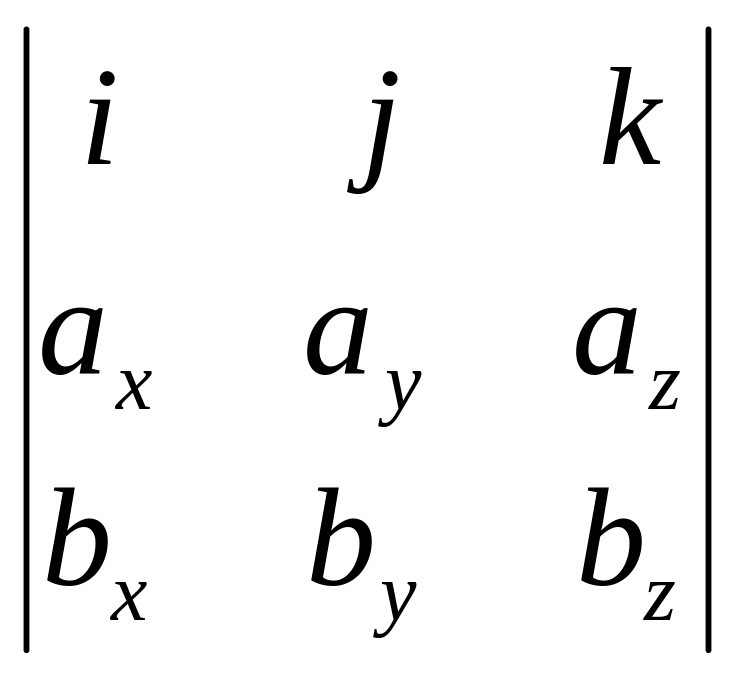∙j
+
∙k
=
,
причём
=
=
∙
,
где
–
угол между векторами
,
(известно:
,
то есть
≥0).
Для векторов , , определено векторно-скалярное, то есть смешанное, произведение: ( x )∙ или ∙( x ). В координатной форме вычисление определяется выражением:
(
x
)∙
=
–
+
=
=
=
.
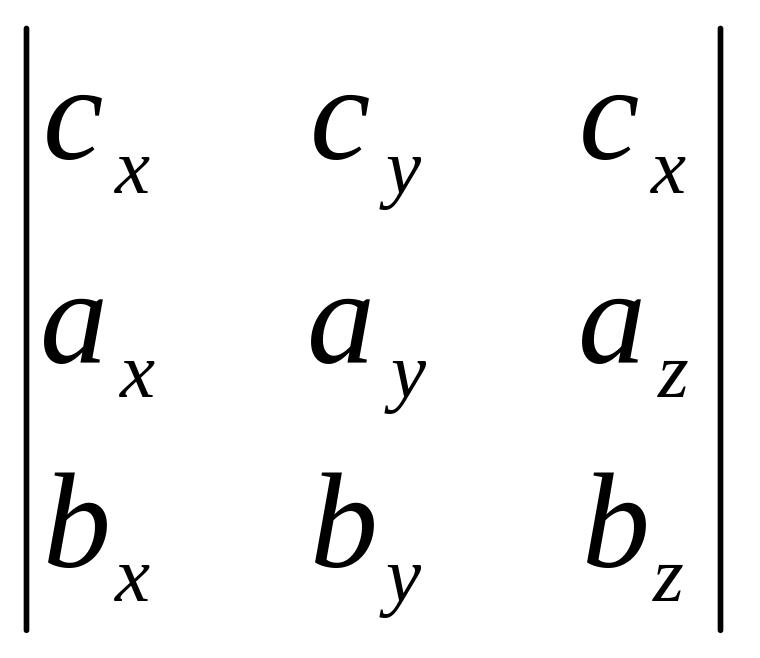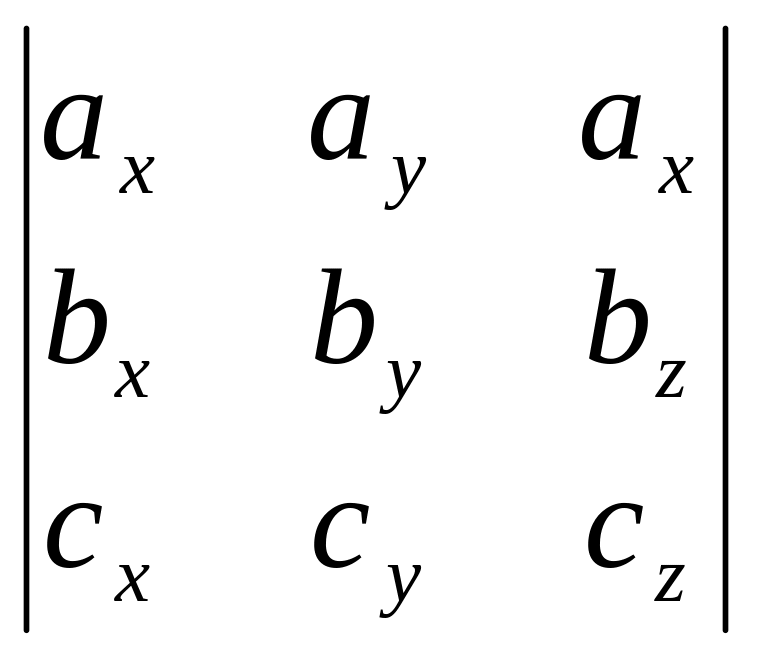Известно,
что векторное произведение обладает
свойствами: 1)
=
,
2)
,
3)
=
+
.
Используют также выражение: |( x )∙ |=| |∙| |∙| |∙ ∙ =|V| – объём параллелепипеда, построенного на векторах , , . Из последнего следует условие компланарности этих векторов: ( x )∙ =0.
••• ≡ •••
Пример
1–98:
Векторы
и
образуют угол
.
Зная, что
,
,
вычислить: 1)
,
2)
,
3)
.
Замечание: применение вместо записи векторов в виде: и предпочтительнее, чем использование записей векторов с индексами (учитывая почерк большинства!).
Решение:
Применяя общие формулы, решим каждую из поставленных задач:
1).
Вычислим:
=
∙
=
=
.
2).
Преобразуем выражение:
=
=3
=3
.
3). Как
в пункте 2):
=
=10
=10
.
Ответ: 1) , 2) 3 , 3) 10 .
Пример
2–106:
Даны векторы
=
(3,–1,2),
=
(1,2,–1).
Найти координаты векторных произведений:
1)
,
2)
,
3)
.
Решение:
Применяя общие формулы, решим каждую из поставленных задач:
1).Воспользуемся
формулой:
,
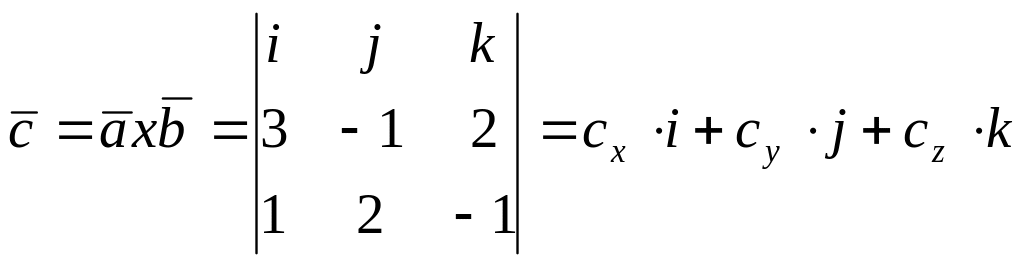где:
,
,
→
.
2). С
учетом результата п. 1:
.
3). С
учетом п. 1:
.
Замечание: преобразования в п. 1), 2), 3) учитывают свойства векторного произведения.
Ответ: 1): (–3,5,7); 2): (–6,10,14); 3): (–12,20,28).
Пример
3–115:
Сила
=(2,–4,5)
приложена к точке
=(4,–2,3).
Определить момент этой силы относительно
точки
=(3,2,–1).
Решение:
О
бщие
формулы: в
физике моментом силы относительно
неподвижной точки называют вектор,
вычисляемый по формуле:
=
x
=
,
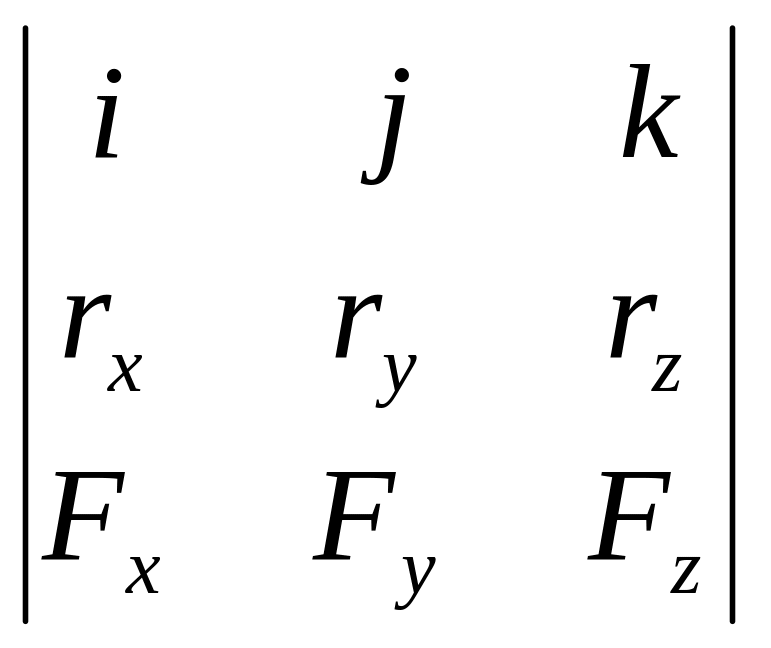где
–
радиус-вектор из точки
в точку
приложения силы
(на самом деле, вместо точки приложения
силы
,
может быть использована любая точка,
принадлежащая линии действия этой
силы).
Применяя общую формулу, запишем решение поставленной задачи:
1).
Вычислим радиус-вектор:
=
=
=(4,–2,3)
–(3,2,–1)= (1,–4,4).
2). Вычислим
вектор момента силы
относительно неподвижной точки
:
=
=
,
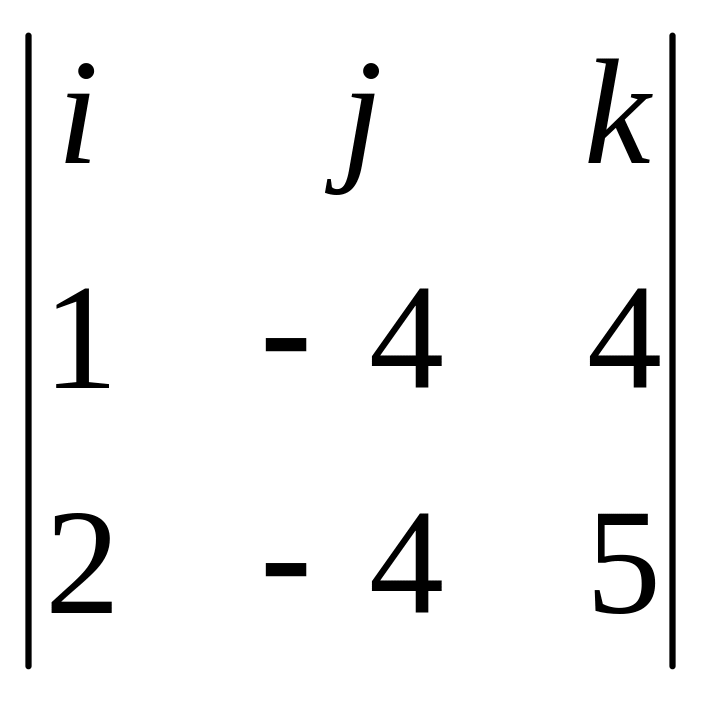где: 
=
=–4,
=–
=–3,
=
=4
→
=(–4,3,4).
Ответ: моментом силы: =(–4,3,4).
Пример 4–127: Установить, образуют ли векторы: , , базис в множестве векторов пространства : 1) = (2,3,–1), = (1,–1,3), = (1,9, –11),
2) = (3,–2,1), = (2,1,2), = (3,–1,–2).
Решение:
Общие
формулы: известно,
что векторы
,
,
образуют базис, то есть независимы, если
они не принадлежат одной плоскости или
параллельным плоскостям; для проверки
этого условия используют определитель
=
:
если
0,
то векторы независимы, если
=0,
то зависимы.
Применяя названный критерий, решим каждую из поставленных задач:
1).
Вычислим определитель:
=
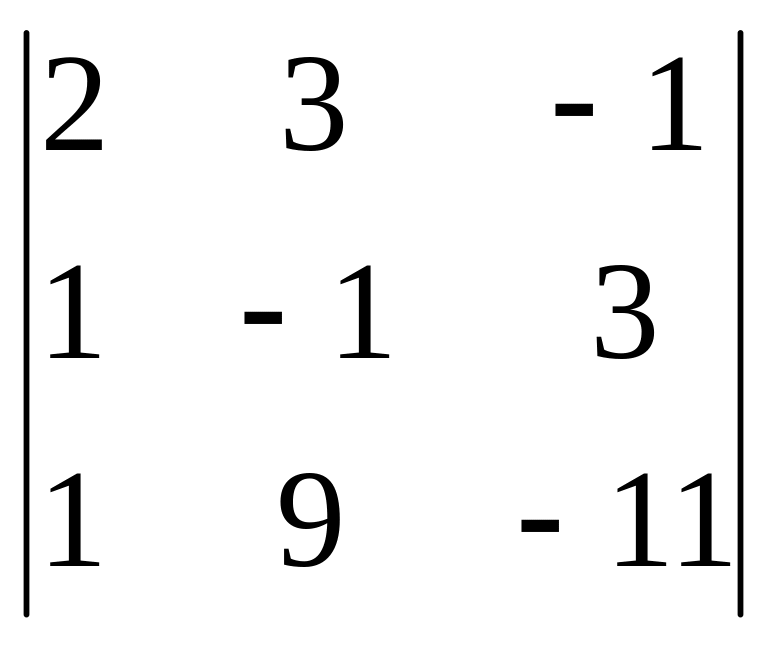=2
–1
+1
=0.
Следует: векторы не образуют базис.
2).
Вычислим определитель:
=
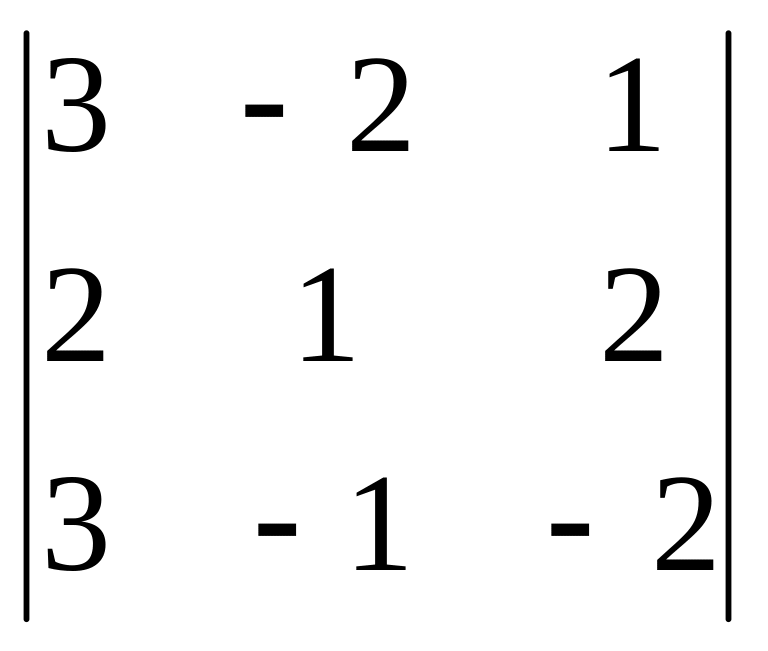=3
–2
+3
0.
Следует: векторы образуют базис.
Ответ: для случаев: а) не образуют, б) образуют.
Пример
5–132:
Вычислить объём
тетраэдра
,
если
=
,
=
,
=
.
Р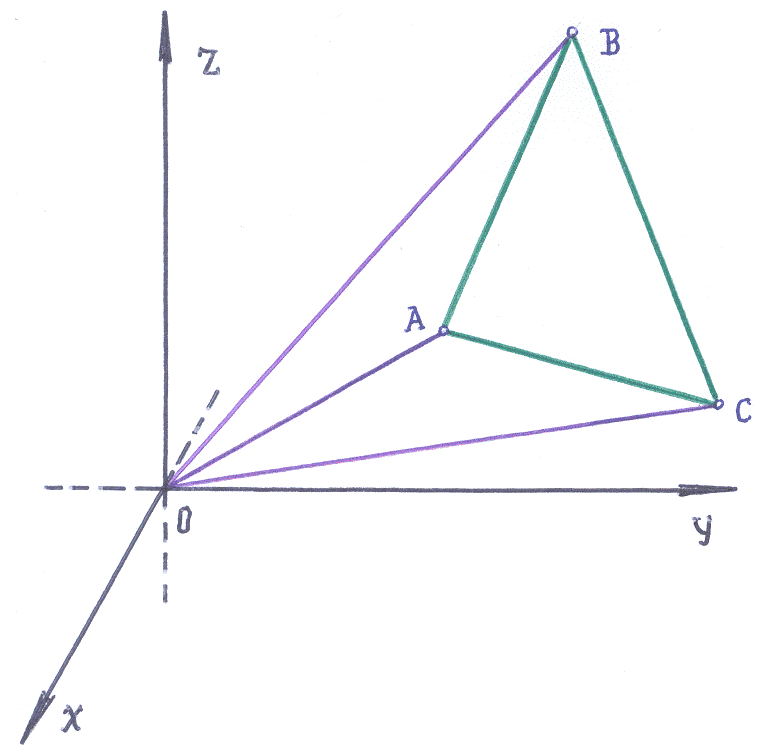
ешение:
Замечание: задачу можно было решать без рисунка (достоинство аналитической геометрии), но мы воспользуемся простым эскизом для побуждения зрительного образа решения задачи.
Алгоритм:
1) вспомним: объём пирамиды равен 1/3 объёма соответствующей призмы;
2)
обозначим объём пирамиды –
,
а объём параллелепипеда, построенного
на векторах
=
,
=
,
=
–
;
вычислим
=
–
величина объёма со знаком;
3)
учтём, что
=6
и запишем результат
=
.
Реализуем принятый алгоритм:
1). Вычислим смешанное произведение векторов , , :
=
=
=3
+0
+0 =–51.
2).
Вычислим объём пирамиды:
=
=
.
Ответ: объём пирамиды: = = .