Санкт-Петербургский государственный электротехнический университет

Кафедра автоматики и процессов управления

Санкт-Петербургский государственный политехнический университет

Кафедра управления проектами

11

Лекция № 6 странные аттракторы. Динамический хаос

Странные аттракторы. Показатели Ляпунова. Детерминированный хаос. Фрактальные объекты, фрактальные аттракторы

1. Странные аттракторы

Аттракторы вида узел, фокус и предельный цикл являются математическими образами установившихся режимов в динамических системах.

Принадлежащие аттрактору траектории устойчивы.

Это свойство позволяет предсказывать поведение таких систем, даже если начальные условия x₀ известны с некоторой погрешностью.

Объекты, получившие название странных аттракторов, открыты в начале 60-х американским метеорологом Э. Лоренцем при исследовании упрощенной математической модели физики атмосферы. Они описывают непериодические хаотические режимы в динамических системах вида

dx/dt = F(x), x(t₀) = x₀ (1)

Странные аттракторы не обладают свойством устойчивости:

пусть x₀ – любое малое отклонение в начале траектории, тогда

||x(t, x₀) – x(t, x₀ + x₀)||  e^t||x₀||,  > 0. (2)

Отсюда следует, что при t  T будет теряться какая-либо информация о положении системы dx/dt = F(x) в фазовом пространстве. Такой вывод означает, что в классическом смысле задачи, связанные с изучением странных аттракторов, не корректны. В корректных задачах теоремы существования и единственности решений выполняются на конечном интервале 0  t  T. Необходимо, чтобы существовала некоторая величина , которая гарантировала бы близость траекторий при 0  t  . Это условие фигурирует в ляпуновской теории устойчивости решений.

Для странного аттрактора такого условия нет.

Это не связано с несовершенством формализма обыкновенных дифференциальных уравнений. Причиной является физическое явление динамического хаоса.

Странные аттракторы являются математическим образом установившегося хаотического поведения в динамических системах.

Странные аттракторы существуют даже в сравнительно простых системах трех дифференциальных уравнений, в правые части которых входят только линейные и квадратичные члены.

1.1. «Странность» странных аттракторов связана с их чувствительностью к начальным данным.

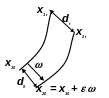
Две близкие точки x₁₀ и x₂₀ , лежащие на аттракторе, отстоят одна от другой на расстояние d₀. Со временем это расстояние меняется d_t = | x_1t – x_2t |.

Если аттрактор – особая точка, то d_t = 0.

Если аттрактор – предельный цикл, то d_t – периодическая функция времени.

Если аттрактор – странный, то d_t = e^t,  > 0.

Чтобы величина  характеризовала аттрактор, надо рассматривать бесконечно близкие траектории и среднюю скорость их разбегания на большом интервале времени.

( x₁₀,  ) = lim lim [(1/t) ln (d_t/d₀)], . (3)

t, d₀0

 - вектор от x₁₀ до x₂₀

Выбирая различные точки х₁₀ и x₂₀ , можно получать разные числа .

В 1968 г. В. Оселедец показал, что при весьма общих условиях почти все точки х₁₀ и x₂₀ в окрестности странного аттрактора в N-мерной динамической системе будут давать один и тот же набор ляпуновских показателей ₁, ₂,… _N.

 - характеризует изменение длины отрезка d_t.= |x_1t – x_2t |.

Изменение площади треугольника с вершинами х_1t, х_2t, х_3t пропорционально

exp (₁ + ₂)t.

₁ - характеризует изменение длины d₁.= |x_1t – x_2t |,

₂ - изменение длины d₂.= |x_2t – x_3t|.

Изменение N-мерного объема пропорционально

exp (₁ + ₂ + _N)t.

N-мерный объем малого элемента в фазовом пространстве N-мерной диссипативной системы для аттракторов сокращается

1  i  N

_i < 0.

Если аттрактор точка или цикл, то, наблюдая за системой достаточно долго, можно дать достоверный прогноз даже, если х_t известен с некоторой ошибкой. Ведь d_t не будет расти.

Положительные ляпуновские показатели и связанная с этим чувствительность к начальным данным заставляют по-иному смотреть на саму возможность предсказания явлений природы. У странного аттрактора через время  1/ две близкие вначале траектории с течением времени перестанут быть близкими.

Существуют фундаментальные ограничения на возможность прогнозов в нелинейных системах.

1.2. «Странность» хаотических аттракторов связана с их геометрическими свойствами. Часто эти объекты имеют сложную структуру, обладающую масштабной инвариантностью. В мелком масштабе они выглядят также, как в крупном.

Вычисление ляпуновских показателей в тех случаях, когда известна функция F(x), достаточно просто осуществляется с помощью компьютера.

Система рассматривается в вариациях.

Пусть известна траектория x(t). Рассмотрим близкую траекторию

x*(t) = x(t) +  t.

Матрица A(x) = D(F(x))/D(x) – матрица системы (якобиан), линеаризованной в окрестности траектории x(t).

Если траектории x(t) и x*(t) бесконечно близки, то членами, квадратичными по (t) можно пренебречь. Отклонение x(t) от x*(t) определяется системой в вариациях для (t):

(t) = A(x(t)) (t), (4)



t

= lim [1/t ||(t)|| / ||₀||], ₀ = (t=0). (5)

Определенный таким образом ляпуновский показатель  эквивалентен заданному выражением (3). Использование формул (4), (5) в расчетах более предпочтительно.

Чтобы определить старший ляпуновский показатель, наряду с исходным уравнением (1) считают систему в вариациях (4).

Чтобы решение (t) не было слишком большим, через определенный интервал времени его перенормируют (делят на достаточно большое число). В соответствии с этим модифицируются формулы (4) и (5).

Перенормировка нужна, чтобы повысить точность определения показателей. Взяв наугад (t=0), обычно находят первый ляпуновский показатель ₁. Чтобы оценить k показателей ₁, ₂, _k, считают k систем в вариациях. Вычисляют k-мерный объем и пользуются соотношениями, аналогичными формуле (5).

Через определенное время приходится выполнять не только перенормировку, но и ортогонализацию, поскольку ₁, ₂, …, _k, с течением времени стремятся повернуться вдоль ₁, соответствующего наибольшему ляпуновскиму показателю.

В настоящее время ляпуновкие показатели являются наиболее эффективно и просто вычисляемыми характеристиками динамического хаоса.