Министерство образования и науки РФ

Санкт-Петербургский государственный горный институт

(технический университет)

Кафедра Общей и технической физики

(лаборатория электромагнетизма)

Лабораторная работа №3

Изучение магнитного поля

(закон Био–Савара–Лапласа)

По дисциплине: Физика

^{(наименование учебной дисциплины согласно учебному плану)}

Выполнил: студент гр. ГМ-10-1 __________ /Татко В.Д./

^{(подпись) (Ф.И.О.)}

Проверил ассистент __________ /Быстров Д.С,/

^{(должность) (подпись) (Ф.И.О.)}

Санкт – Петербург

2011

Цель работы: Измерение магнитных полей, создаваемых проводниками различных конфигураций. Экспериментальная проверка закона Био–Савара–Лапласа.

1. Магнитное поле прямолинейного проводника с током

Проводник, по которому протекает электрический ток, создает магнитное поле. Магнитное поле характеризуется вектором напряженности H (рис. 1), который можно вычислить по формуле

H = dH.

Cогласно закону Био-Савара-Лапласа,

,

где I – сила тока в проводнике, dl – вектор, имеющий длину элементарного отрезка проводника и направленный по направлению тока, r – радиус вектор, соединяющий элемент с рассматриваемой точкой P.

Р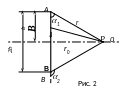 ассмотрим магнитное поле, создаваемое прямолинейным проводником с током конечной длины (рис. 2). Отдельные элементарные участки этого проводника создают поля dH, направленные в одну сторону (перпендикулярно плоскости чертежа), поэтому напряженность магнитного поля в точке P может быть найдена интегрированием:

Имеем l = r_oсtg, так что Кроме того, Поэтому

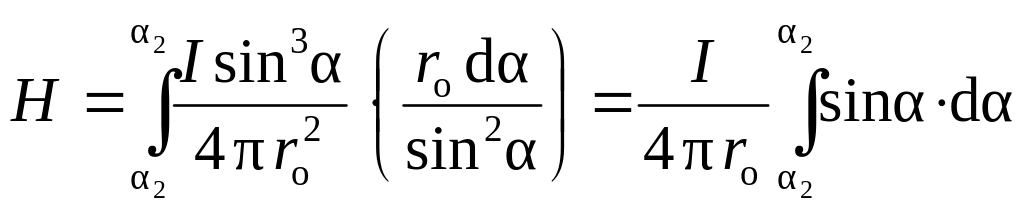
После интегрирования получим

, (1)

где r_o – кратчайшее расстояние от точки P до проводника с током, ₁ и ₂ – углы между крайними элементами проводника и соответствующими радиус-векторами PA и PB.

Если определять напряженность в точках, расположенных на перпендикуляре, восстановленном к середине проводника, то cos₂ = cos(180 – ₁) = –cos₁ и, следовательно,

(cos₁ – cos₂) = 2cos₁ =  . (2)

С учетом выражения (2) формулу (1) можно записать в виде

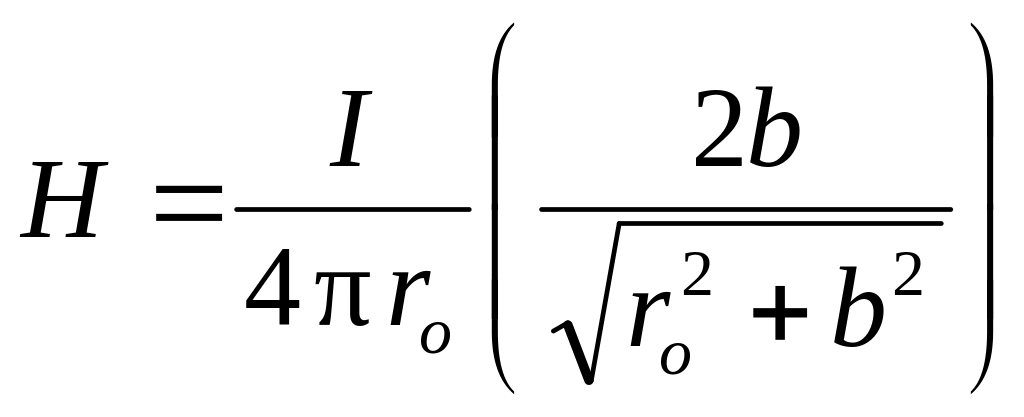. (3)

Учитывая, что в настоящей работе длина проводника 2b много больше расстояния r₀ от проводника до точки наблюдения магнитного поля, формулу (3) можно записать в виде

. (4)

Поэтому индукция магнитного поля рассчитывается по формуле:

, (5)

где ₀ – магнитная постоянная,  – магнитная проницаемость среды (для воздуха  = 1)

2. Магнитное поле на оси короткой катушки с током

Проводник, по которому протекает электрический ток, создает магнитное поле которое характеризуется вектором напряженности H (рис. 3). Напряженность магнитного поля подчиняется принципу суперпозиции

а, согласно закону Био-Савара-Лапласа,

, (6)

где I – сила тока в проводнике, – вектор, имеющий длину элементарного отрезка проводника и направленный по направлению тока, r – радиус вектор, соединяющий элемент с рассматриваемой точкой P.

Одной из часто встречающихся конфигураций проводников с током является виток в виде кольца радиуса R (рис. 3, а). Магнитное поле такого тока в плоскости, проходящей через ось симметрии, имеет вид (см. рис. 3, б). Поле в целом должно иметь вращательную симметрию относительно оси z (рис. 3, б), а сами силовые линии должны быть симметричны относительно плоскости петли (плоскости xy). Поле в непосредственной близости от проводника будет напоминать поле вблизи длинного прямого провода, так как здесь влияние удаленных частей петли относительно невелико. На оси кругового тока поле направлено вдоль оси Z.

В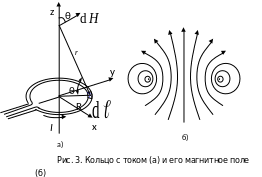 ычислим напряженность магнитного поля на оси кольца в точке расположенной на расстоянии z от плоскости кольца.

По формуле (6) достаточно вычислить z-компоненту вектора :

. (7)

Интегрируя по всему кольцу, получим dl = 2R. Поскольку, согласно теореме Пифагора r² = R² + z², то искомое поле в точке на оси по величине равно

. (8)

Направление вектора H может быть направлено по правилу правого винта.

В центре кольца z = 0 и формула (8) упрощается:

(9)

Нас интересует короткая катушка – цилиндрическая проволочная катушка, состоящая из N витков одинакового радиуса. Из-за осевой симметрии и в соответствии с принципом суперпозиции магнитное поле такой катушки на оси H представляет собой алгебраическую сумму полей отдельных витков H_i: . Таким образом, магнитное поле короткой катушки, содержащей N_к витков, в произвольной точке оси рассчитывается по формулам

, , (10)

где H – напряженность, B – индукция магнитного поля.