2. Постановка задачи на программирование
Задача 1
Заполнение таблицы истинности и построение СДНФ
Исходные данные:
В диалоге вводится количество переменных, строится соответствующая таблица истинности. В двоичном коде вводятся точки логического пространства, в которых функция равна 1.
Алгоритм:
В таблице предусмотрены пустые строки (минитермы, слагаемые), которые будут заполняться вручную. Итоговое выражение получается автоматически как конъюнкция, дизъюнкция, сумма по модулю 2 и т.д. этих строк.
Вывод:
Сообщение о результат расчетов выводится на экран и/или в текстовый файл.
Примечание:
Один из загружаемых файлов – функция из задания.
Задача 2
Минимизация функции при помощи карты Карно.
Исходные данные:
Карта Карно заполняется вручную, из файла или из таблицы истинности.
Алгоритм:
Вручную пользователь определяет, какие ячейки карты Карно он хочет обвести общим овалом. Обведенные ячейки выделяются цветом. В случае, Если не все выбранные ячейки содержат 1 или нельзя обводить группу подобной конфигурации, программа выдает сообщение об ошибке.
Вывод:
Сообщение о результат расчетов выводится на экран и/или в текстовый файл. Один из загружаемых файлов – функция из задания.
2.2 Описание разработанного объекта
2.2.1 Иерархия наследования
Для работы с графами мною создан собственный класс tbool, который имеет следующую структуру:
type
tbool=class
private
fn:integer;
fa:array of array of integer;
fb:array of array of integer;
fc:array of array of integer;
a1:array of array of integer;
a2:array of array of integer;
b1:array of array of integer;
b2:array of array of integer;
fi:integer;
fj:integer;
fk:integer;
procedure seti(const value:integer);
procedure setj(const value:integer);
procedure setk(const value:integer);
procedure setn(const value:integer);
public
property i:integer read fi write seti;
property j:integer read fj write setj;
property k:integer read fk write setk;
function cikl:boolean;
function vydelenie:boolean;
function fmin:integer;
procedure setab;
procedure setc;
procedure obnul;
procedure setvalue1;
procedure setvalue3;
procedure setvalue2(const value:integer);
property n:integer read fn write setn;
function Getvalue1(ind1,ind2:integer):integer;
function Getvalue2(ind1,ind2:integer):integer;
function Getvalue3(ind1,ind2:integer):integer;
end;
Разработанный класс наследование от TStringGrid, рис.2.1.
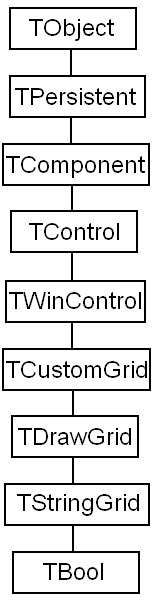
Рисунок 2.1 – Иерархия наследования моего класса.
2.2.2. Организация объекта
Для данного класса реализованы идеи инкапсуляции, включая инкапсуляцию, основанную на разделах private и public. Основное внимание уделено инкапсуляции, основанной на свойствах. Сокрытой частью класса является раздел private, в котором определены:
поле Fn – содержит количество элементов динамически создаваемых массивов (по сути – количество вершин в графах);
поля Fa, Fb, Fc – двумерные динамические массивы целых чисел (указатели на массивы целых чисел) предполагают работу с координатами вершин, ребрами графа;
методы SetI, SetJ, SetK и SetN реализуют инициализацию полей Fi, Fj, Fk и Fn. Правило гласит, что доступ к полям класса должны осуществлять только методы данного класса.
Данное ограничение легко реализуется с помощью механизма свойств, которые описаны в разделе public и являются общедоступными. Наиболее часто применимая конструкция свойств – это отражение чтения данных на поле класса, а запись на метод класса (обычно при записи данных осуществляется дополнительная проверка контроля). Например:
property i:integer read fi write SetI
Методы класса реализуются с помощью процедур и функций. В общедоступном разделе public содержатся следующие методы:
function cikl:boolean; – определение наличия циклов;
function ejler:boolean; – проверка, является ли граф эйлеровым;
function fmin:integer; – минимальная степень графа;
procedure obnul; – обнуление числовых матриц графа.