1.2. Пределы иррациональных выражений

Пример 1. Пр. 4, Пр. 2

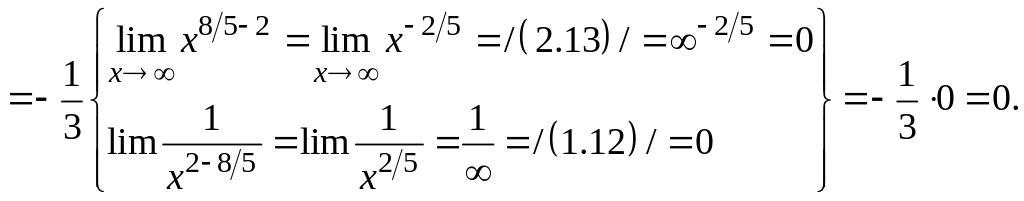
Примечание. При вычислении пределов иррациональных выражений, дающих неопределенности типа или используют введение новой переменной, освобождающей от иррациональности, или преобразование выражения с помощью сопряженного ему. Например, парами взаимно сопряженных выражений будут:

1) и

2) и

3) и которые при вычислении пределов используются в формах:

(1.6)

(1.7)

(1.8)

Пример 2. Пр.6

Пример 3.

Пример 4.

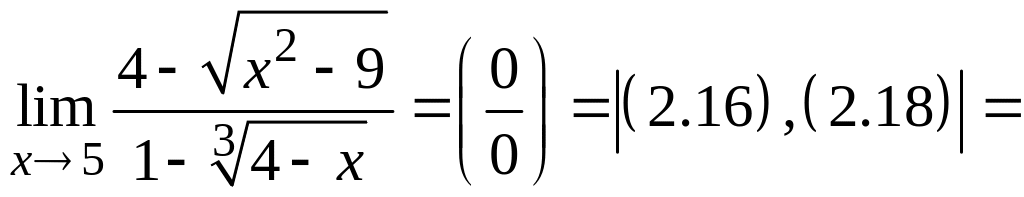
Примечание. Обратите внимание на то, что при вычислении предела 5 из пункта 2.4.I и 3,4 настоящего пункта, при раскрытии неопределенности и стараются так преобразовать выражение, чтобы дробь можно было сократить на множители стремящийся к нулю.

1.3. Вычисление пределов с использованием таблицы эквивалентных бесконечно малых функций.

Пример 1. Пр.2 Пр. 3

Пример 2. EMBED Equation.DSMT4

Пример 3. Пр. 2

Пример 4.

Пример5. Пр.4,Пр.6 Пр.6

Пример 6. 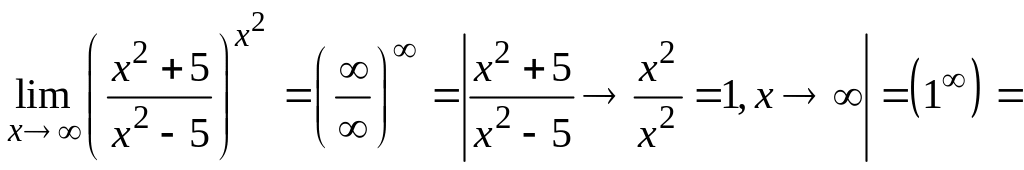(Пр.5)=

Пример 7.

Пример 8.

Пример 9. не определен из-за знака

1)

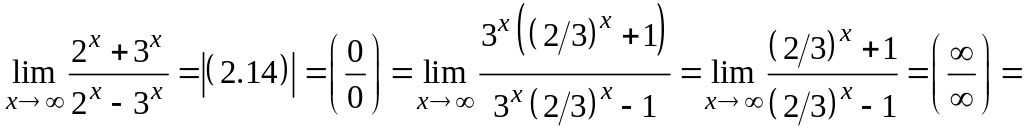
2) Пр.4

Таким образом, существуют различные односторонние на и на пределы.

1.4. Указания к заданию 5.

Пример. Докажите, что

и

бесконечно малые функции одного порядка при Найдите значение постоянной “C”, при котором они будут эквивалентны.

Решение.

Пр.

Пр. Пр.3 при

1.5. Пример выполнения задания 5.

Определите порядок относительно “x” функции

бесконечно малой при

Решение.

при

- бесконечно малая одного порядка по отношению к , то сеть второго порядка относительно “x”.

1.6. Указания к выполнению задания 7.

При исследовании функции на непрерывность пользуются теоремой о непрерывности элементарных функций там, где они определены; признаком непрерывности фуки в точке когда

(2.19)

При наличии точек разрывов исследуют функции в их окрестности и соответствующим образом классифицируют.

Пример 1. Исследовать функцию на непрерывность и построить её схематический график, если

Решение. Сначала найдем область определения функции

Область определения симметрична относительно начала координат, следует исследовать функцию на признак четности.

функция нечетная и её график симметричен относительно начала координат. Таким образом, достаточно исследовать функцию на промежутке построить график, а затем отобразить его симметрию начала координат.

1. В точке функция определена справа, поэтому найдем лишь правосторонний предел в ней:

- точка бесконечного разрыва (П-рода), не входит в

2. На получим

график приближается к оси OX ( =0) снизу при

3. Для уточнения графика найдем дополнительную точку

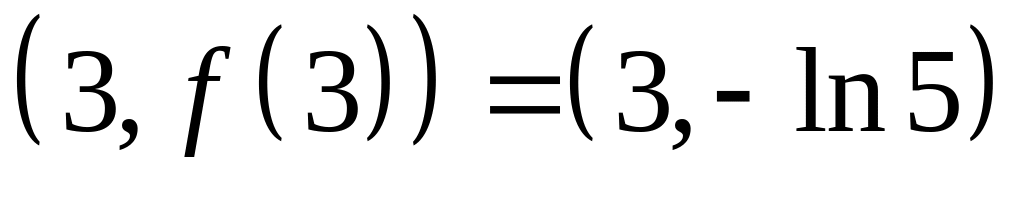
Заданная функция элементарная, и область её непрерывности совпадает с областью определения

- область непрерывности.

Строим график для а затем достраиваем для