Министерство образования и науки рф

Волгоградский государственный технический университет

Кафедра «высшая математика»

Введение в математический анализ

Методические указания

Волгоград

2009

УДК 514.742.4(075)

Рецензент

Печатается по решению редакционно-издательского совета

Волгоградского государственного технического университета

Введение в математический анализ: метод. указания/ сост.

ВолгГТУ. – Волгоград, 2009 - с.

Работа содержит методические указания к выполнению типового расчета по теме «Введение в анализ», вопросы к зачету по теме, варианты заданий, приведены решения типовых задач.

© Волгоградский государственный

технический университет, 2009

Настоящие методические указания предназначены для студентов всех специальностей первого курса. По теме «Введение в математический анализ» необходимо выполнить индивидуальное задание и сдать теоретический зачет.

1. Методические указания к выполнению заданий

Введение

Вычисление пределов функций начинают с непосредственной подстановки предельного значения основной переменной в выражении для функции, используя правила предельного перехода под знаком непрерывной функции, теоремы о пределах. Если получают неопределенности:

используют различные приемы их «раскрытия».

Ниже приведенное правило дет некоторые свойства бесконечно малых и бесконечно больших функций, связь между ними.

Правило 1.

Если

- (постоянная величина),

- ограниченная функция,

- бесконечно малая функция (или короче “0”),

- бесконечно большая функция, то

1) 2) ( - одного знака);

3) 4)

5) 6)

7) 8)

9) 10)

11) 12)

Таблица эквивалентных бесконечно малых функций при

Примечание. Приближенными равенствами 6 и 8 пользуется в другой форме при

Правило 1.

При нахождении предела отношения бесконечно малых при бесконечно больших функций каждую из них (или одну) можно заменить другой функцией, ей эквивалентной. То есть:

(1.1)

Правило 2.

Алгебраическая сумма бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.

Правило 3.

Алгебраическая сумма бесконечно больших функций разных поряд-ков эквивалентна слагаемому высшего порядка.

Правило 4.

При вычислении предела показательно-степенной функции где и

пользуются равенством:

(1.2)

Правило 5.

Неопределенности вида или приводят к виду дроби, которая может дать новые – типа или .

Часто используются при вычислении пределов следующие свойства показательной и степенной функции:

(1.3)

(1.4)

(1.5)

1.1. Пределы рациональных функций

Пример 1.

(Пр.4); Пр.2 Пр. 1.8

Пример 2. Пр. 1.11 Пр. 6 Пр. 1.11

Пример 3. 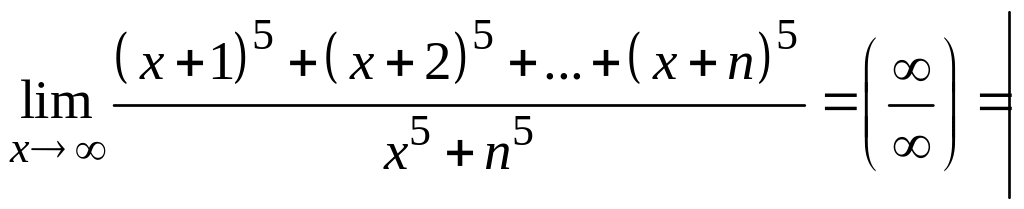Пр. 4, Пр.2

Пример4. Пр.6 Пр.4,Пр.2

Примечание. Если бы мы воспользовались вначале последовательно правилами 4 и 2, то получили бы:

что неверно, так как разность эквивалентных бесконечно больших функций есть функция более низкого порядка, чем каждая из них (бесконечно большая, постоянная) как в рассмотренном примере, или, в крайнем случае, предел их разности может быть бесконечно малой функцией (см. пример 2 пункта. 2.4.2).

Пример 5. /разложим многочлены на множители/=