Электронные конфигурации атомов и периодичность свойств химических элементов

Элементарные сведения о квантово-механической модели строения атома

К началу 20 века было открыто множество явлений прямо или косвенно свидетельствующих о сложном строении атомов (фотоэффект^*, радиоактивность^** и т.д.). Возник вопрос: как устроен атом? Наиболее удачная модель строения атома была предложена в 1911 г английским физиком Эрнестом Резерфордом.

• Фотоэффект - испускание электронов металлами и полупроводниками при их освещении.

• Радиоактивность – самопроизвольный распад атомов, сопровождающийся испусканием различных частиц.

Вокруг положительно заряженного ядра, в котором сосредоточена основная часть массы атома, вращаются электроны. Подобную модель называют ядерной. Радиус атома приблизительно оценивается величиной 10^-10 м, а ядра 10^-15 м. Согласно классической электромагнитной теории, система, состоящая из массивного положительно заряженного ядра (1,67 ּ 10^-27 кг для атома водорода) и лёгких (масса электрона 9,1 ּ 10^-31 кг) отрицательно заряженных электронов (электрон в 1835 раз легче ядра), может быть устойчивой лишь при условии, если электрон находится в движении. Однако непрерывно движущийся электрон (скорость движения электрона 10⁸ м/с) должен непрерывно излучать энергию и соответственно израсходовать её за ничтожную долю секунды. Однако атом водорода устойчив. Следовательно, такая модель неверна. В 1913 г Нильс Бор (Дания) предположил, что электрон движется не по любым, а лишь по строго определённым («разрешённым») орбитам. Энергия электрона теряется лишь при переходе между двумя «разрешённым» орбитами. Так был и заложены принципы квантования энергии электрона.

В 1924 г французский учёный Луи де Бройль высказал предположение о волновом характере материи. Согласно де Бройлю материальному объекту с импульсом mv отвечает длина волны λ . Количественная взаимосвязь между волновыми и корпускулярными свойствами материи выражена уравнением де Бройля:

, где

h – постоянная Планка, равная 6,626 ּ10^-34 Дж ּс,

m и – масса и скорость частицы.

Для макрообъектов длина волны крайне мала из-за относительно большой массы. Например, для винтовочной пули массой 0,025 кг, движущейся со скоростью 9ּ10² м/с длина волны равна 2,94 ּ10^-31 м. Для электрона при скорости движения 3 ּ10⁸ м/с - 2,4 ּ10^-10 м, а это уже размеры атома.

Матер. объект	Масса, кг	Скорость, м/с	Длина волны, м
Человек Винтовочная пуля	90 0,025	3 9 ּ 104	2,4∙10-36 2,94 ּ 10-35
Электрон	9,1 ּ 10-31	3 ּ 108	2,4 ּ 10-10

Таким образом, в макромире мы не замечаем волновых свойств материи. Электрон же можно рассматривать и как частицу, и как волну. Предположение де Бройля в дальнейшем подтвердилось – была обнаружена дифракция электронов, а впоследствии и дифракция нейтронов.

Описанием поведения микрочастиц занимается квантовая механика. В 1926 г Гейзенбергом сформулирован принцип неопределённости: невозможно одновременно с одинаково большой степенью точности указать положение микрочастицы и её импульс. В математической форме принцип неопределённости может быть выражен соотношением:

Δp ּ Δq ≥ h/2π, где

Δp – неточность измерения импульса (mv);

Δq - неточность измерения координаты частицы.

Можно оценить лишь вероятность нахождения электрона в том или ином месте пространства. Оценка этой вероятности проводится математически при помощи волнового уравнения Шрёдингера (1926 г). (Эрвин Шрёдингер – австрийский физик):

НΨ = ЕΨ, где

Н - оператор Гамильтона (математический символ, указывающий, какие действия следует осуществить над функцией, стоящей под знаком оператора);

Е – энергия электрона.

Ψ – волновая функция. Определённый физический смысл имеет её квадрат Ψ², который характеризует вероятность нахождения электрона в данной точке атомного пространства. Величина Ψ² ∆V представляет собой вероятность обнаружения электрона в элементе объёма ∆V (её называют орбиталью электрона).

Уравнение Шрёдингера имеет не одно, а набор решений:

Ψ_1, Ψ₂, Ψ₃, …, которым соответствуют энергии электрона:

Е₁, Е₂, Е₃, … , т.е. энергия электрона принимает не любые, а строго определённые значения (ряд дискретных «разрешённых» энергий). Таким образом, мы вновь говорим об энергетических уровнях, т. е. пришли к идее квантования энергии, но уже с точки зрения квантовой механики.

Ψ – волновая функция, соответствующая амплитуде трёхмерного волнового процесса Ψ = Ψ(x,y,z), где x,y,z – координаты точки. Поэтому результатом решения уравнения Шрёдингера является комбинация некоторых параметров (набор целых чисел n, l, m_l), которые называют квантовыми.

Ψ Ψ(x,y,z) n, l, m_l

Квантовые числа n, l, и m_l определяют геометрические особенности электронного облака.(Электрон в атоме представляет собой трёхмерную колеблющуюся систему, ему соответствует трёхмерная стоячая волна. Очевидно, что для описания пространственного движения электрона в атоме нужны три и только три квантовых числа.).

Квантовые числа

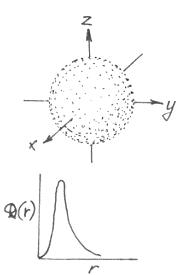
n - главное квантовое число, определяет энергию электрона и расстояние его наиболее вероятного нахождения вблизи ядра (размеры электронного облака). Принимает целочисленные значения n = 1, 2, 3,…¥

Чем больше n, тем больше энергия электрона и тем большие размеры имеет его электронное облако.

n = 1, 2, 3,…¥

э нергия увеличение

р азмеры электр.облака увеличение

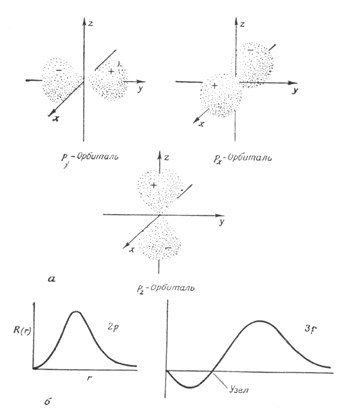
l - орбитальное квантовое число, определяет момент количества движения электрона (векторная величина). Принимает значения:

l = 0,1,2,3…(n-1);

определяет форму электронного облака (орбитали) и характеризует запас энергии электрона в энергетическом подуровне.

Для удобства вместо числовых значений l употребляются буквенные:

Значение l 0 1 2 3 4 …

Символ орбитали s p d f q …

Энергия орбиталей, которые находятся на одном энергетическом уровне, но имеют различную форму, неодинакова.

E_s < E_p < E_d < E_f …

Главное и орбитальное квантовые числа

n = 1,2, 3,4…	l от 0…до(n-1)	Обозначение подуровня	Число подуровней на уровне (равно n)	Число орбиталей на уровне (равно n2)
1	0	1s	1	1
2	0 1	2s 2p	2	4
3	0 1 2	3s 3p 3d	3	9
4	0 1 2 3	4s 4p 4d 4f	4	16

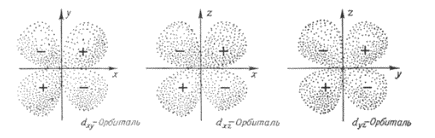
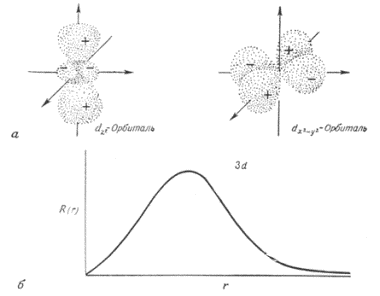
m_l - магнитное квантовое число, определяет проекцию вектора момента количества движения на направление магнитного поля. Значения m_l характеризуют разрешённые ориентации электронного облака в пространстве (m_l = -l …0…+l).

Орбитальное и магнитное квантовые числа

l подуровень	ml (-l…0…+l) всего 2l+1 значений	Число АО на подуровне 2l+1	Графическое изображение АО
0 (s)	0	1
1 (p)	-1,0,+1	3
2 (d)	-2,-1,0,+1,+2	5
3 (f)	-3,-2,-1,0,+1,+2,+3	7

Когда эти три квантовых числа определены, волновая функция описывает конкретный электрон и обычно называется атомной орбиталью (мы говорим, что задана орбиталь).

Форма s,p,d-орбиталей:

Изучая атомные спектры, установили, что электрон имеет еще и собственный момент количества движения, который был назван спином (to spin - вращать); квантовое число его определяющее (m_s) может иметь только два значения: +1/2 и -1/2. (­¯). Необходимость введения четвёртого квантового числа не связана с решением уравнения Шрёдингера.

Принципы заполнения электронами энергетических уровней и подуровней в атоме: принцип минимума полной энергии атома, принцип Паули, правила Гунда и Клечковского.

Распределение электронов в атоме, находящихся в основном состоянии, определяется зарядом ядра. При этом заполнение электронами энергетических уровней, подуровней и орбиталей происходит в той последовательности, при которой формируются электронные конфигурации, соответствующие минимуму полной энергии атома и наибольшей связи электронов с ядром.

Реализуется этот принцип, если соблюдаются принцип Паули, правило Гунда и правила Клечковского.

1. Принцип Паули: в системе (атоме) не может быть двух электронов, характеризующихся одним и тем же набором четырех квантовых чисел. Или: на одной орбитали могут находиться только два электрона с противоположными спинами.

+1/2



-1/2

неправильно

+1/2



-1/2

правильно

2. Правило Гунда: заполнение электронами данного энергетического подуровня происходит таким образом, чтобы суммарный спин электронов по абсолютной величине был максимальным.

Например, p – орбиталь заполняется:

p_x p_y p_z

↓

↑

↓

↓↑

↑

p_x p_y p_z

-1/2 +1/2 -1/2 -1/2 +1/2 +1/2

Σspin = 1/2 Σspin = 1/2 неправильно

↑

↑

↑

p_x p_y p_z p_x p_y p_z

↓

↓

↓

+1/2 +1/2 +1/2 -1/2 -1/2 -1/2

Σspin = 3/2 Σspin = 3/2 правильно

3. Последовательность заполнения электронами энергетических состояний в атоме определяется правилами Клечковского:

1) заполнение электронами орбиталей происходит в порядке возрастания суммы (n+l);

2) при равенстве суммы (n+l) - в порядке увеличения главного квантового числа n.

Орбитали	n	l	n+l
1s	1	0	1
2s	2	0	2
2p	2	1	3
3s	3	0	3
3p	3	1	4
3d	3	2	5
4s	4	0	4
4p	4	1	5
4d	4	2	6
4f	4	3	7
5s	5	0	5

Последовательность заполнения электронами уровней и подуровней:

1s²2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁶5s²4d¹⁰5p⁶6s²5d¹4f¹⁴5d^2-106p⁶7s²6d¹5f¹⁴6d^2-107p⁶…

Не вдаваясь в детали:

… 6s² 4f¹⁴5d¹⁰6p⁶7s²5f¹⁴6d¹⁰7p⁶…

Теперь можно составлять электронные формулы любых атомов, если известно количество электронов.

Малые периоды на примере элементов ІІІ периода:

Полная электронная формула атома натрия: ₁₁Na 1s²2s²2p⁶3s¹

Сокращённая: [Ne]3s¹ (…3s¹)

Электронные формулы других атомов: ₁₄Si [Ne]3s²3p²; ₁₅P [Ne]3s²3p³

₁₈Ar [Ne]3s²3p⁶

Большие периоды на примере элементов ІV периода:

₁₉K [Ar]4s¹ ₂₁Sc [Ar]4s²3d¹ ₂₃V [Ar]4s²3d³ ₂₆Fe [Ar]4s²3d⁶

₃₀Zn [Ar]4s²3d¹⁰ ₃₁Ga[Ar]4s²3d¹⁰4p¹ ₃₆Kr [Ar]4s²3d¹⁰4p⁶

«Проскок» электрона»

Атом	По положению в ПС	С учётом «проскока»
Cr Mo	…4s23d4 …5s24d4	…4s13d5 …5s1 4d5
Сu Ag	…4s23d9 …5s24d9	…4s13d10 …5s14d10

Электронно-графическая формула:

C

↑

↑

↑

↑

↑

↑

↑

r

4s 3d 4p возрастание Е

C

↑

↑

↑

↑

↑

↑

r

3d 4s 4p возрастание n