3. Виды вычислительных процессов

Различают три вида вычислительных процессов:

• линейные или простые,

• разветвляющиеся,

• циклические.

Линейным называют такой вычислительный процесс, при котором все операции выполняются последовательно, в одном направлении.

Пример: вычислить значение функции y = k(ax² + bx – c) при различных значениях параметров a, b, c, k, x.

На рис. 2. приведен алгоритм линейного вычислительного процесса. Как видно из рисунка все операции алгоритма выполняются последовательно и в одном направлении. Алгоритм применим для вычисления функции y при любых значениях a, b, c, k, x, следовательно, он обладает массовостью, не может быть двояко истолкован (обладает определенностью), всегда приводить к конечному результату (результативный).

Разветвляющимся называют такой вычислительный процесс, у которого на отдельных участках часть операций могут в зависимости от какого–либо условия выполняться различными путями, в одном или другом направлении.

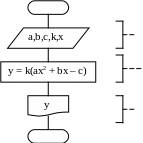
Ввод значений

a, b, c, k, х

Вычисление

функции y

Распечатка

результата

Рис. 2. Линейный вычислительный процесс

Примером разветвляющего вычислительного процесса может служить алгоритм вычисления корней квадратного уравнения, приведенного на рис. 1. Из того алгоритма видно, что после проверки условия d >= 0, в зависимости от его результата, дальнейшие вычисления могут происходить по ветви (+) или ветви ( – ).

Циклическим называют такой вычислительный процесс, в котором многократно (циклически) повторяется некоторая операция или группа операций, называемая телом цикла.

Выполнение любого цикла требует реализации следующих этапов:

• подготовка цикла, предполагающая инициализацию (установления начального значения) регулярно изменяющейся переменной, называемой параметром цикла;

• управление циклом, предусматривающее проверку условия выполнения цикла;

• выполнение тела цикла, означающее выполнение одних и тех же операций для каждого нового значения параметра цикла;

• продвижение цикла, предписывающее изменение параметра цикла на одну и ту же величину, называемую шагом, перед каждым новым выполнением тела цикла.

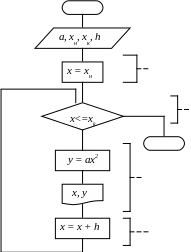
Пример. Вычислить значения функции y = ax², если а = 1.8, а х изменяется от х_н = -3.2 до х_к = 4.3 с шагом h = 0.1.

Блок – схема вычислений (рис.3) предполагает использование циклической операции.

Подготовка цикла

Управление

– циклом

+

Тело цикла

Продвижение

цикла

Рис. 3 Блок – схема циклического вычислительного процесса

Циклическая операция будет выполняться до тех пор, пока будет выполняться условие х <= x_k.

Следует отметить, что в большинстве реальных задач алгоритмы представляются как комбинация различных видов вычислительных процессов.

7