
Введение
Настоящее пособие имеет своей задачей оказать помощь студентам дневного и заочного отделений инженерно-технических специальностей в изучении курса физики.
Физика является наукой о наиболее общих законах природы, о наиболее общих формах движения материи. Занимая центральное место среди других наук в объяснении законов природы, физика имеет первостепенное значение в формировании научного мировоззрения.
Систематическое решение задач является необходимым условием успешного изучения физики. Решение задач помогает уяснить физический смысл явлений, закрепляет в памяти формулы, прививает навыки практического применения теоретических знаний.
При решении задач необходимо:
Указать основные законы и формулы, на которых базируется решение задачи, дать словесную формулировку этих законов, а также указать значение буквенных обозначений, употребленных при написании формул. Не следует пользоваться формулами, полученными для частного случая и не выражающими какой-либо закон.
Физические задачи весьма разнообразны и дать единый рецепт их решения невозможно. Однако, как правило, физические задачи следует решать в общем виде, т.е. в буквенных выражениях. При этом способе не производятся вычисления промежуточных величин; числовые значения подставляются только в окончательную (рабочую) формулу, выражающую искомую величину.
Сделать чертеж, поясняющий содержание задачи, если необходимо.
Сопровождать решение задачи краткими, но исчерпывающими пояснениями.
Подставить в окончательную формулу числовые значения, выраженные в единицах СИ. Несоблюдение этого правила приводит к неверному результату.
Проверить, даст ли рабочая формула правильную размерность величины. Для этого в рабочую формулу следует подставить размерность всех величин и произвести необходимые действия. Если полученная таким путем размерность не совпадает с размерностью искомой величины, то задача решена неверно.
Произвести вычисление величин, подставленных в формулу и записать в ответе числовое значение и сокращенное наименование или размерность единицы измерения искомой величины. Вычисления следует производить приближенно.
Пример решения задач
Пример. Через блок, выполненный в виде диска и имеющий массу m=80 г, перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами m1=100 г. и m2=200 г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь.
Решение. 1-ый способ. Применим к решению задачи основные законы поступательного и вращательного движения. Для этого рассмотрим силы действующие на грузы в отдельности и на блок. На каждый из движущихся грузов действует две силы: сила тяжести P=mg, направленная вниз, и сила натяжения нити Т, направленная вверх (рис.1,а). Спроектируем эти силы на ось х, которую направим вертикально вниз, и напишем уравнение движения в координатной форме.
r


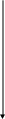


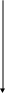
m
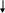
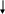
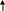
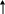
m1
m2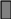
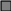
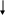
x
Груз m1 поднимается вверх, следовательно, Т1>m1g. По второму закону Ньютона равнодействующая этих сил, равная их разности, прямо пропорциональна массе груза и ускорению, с которым он движется, т.е.:
-Т1 + m1g = -m1a (1)
откуда
T1= m1g + m1a (2)
Груз m2 ускоренно опускается вниз, следовательно, T2<m2g. Запишем формулу второго закона Ньютона для этого груза:
m2g -T2 = m2a (3)
откуда
T2 = m2g - m2a (4)
Cогласно основному закону динамики вращательного движения, вращательный момент М, приложенный к диску, равен произведению момента инерции I диска на его угловое ускорение :
M = I (5)
Определим вращающий момент. Силы натяжения нитей действуют не только на грузы, но и на диск. по третьему закону Ньютона силы Т1' и Т2', приложенные к ободу диска, по величине равны соответственно силам Т1 и Т2, но по направлению им противоположны. При движении грузов диск ускоренно вращается по часовой стрелке, следовательно, Т2'>T1'. Вращающий момент, приложенный к диску, равен произведению разности этих сил на плечо, равное радиусу диска, т.е.:
M = (T2'-T1')r (6)
Момент инерции диска:
I=mr2/2 (7)
Угловое ускорение связано с линейным ускорением грузов соотношением:
= a/r (8)
Подставив в формулу (5) выражения M, I и , получим:
(Т2'-T1')r = (mr2/2)(a/r) (9)
откуда
T2' -T1' = ma/2 (10)
Так как Т1'=T1 и Т2'=T2, то можно заменить силы T1' и Т2' выражениями по формулам (2) и (4), тогда:
m2g -m2a -m1g -m1a = ma/2 (11)
или
(m2 -m1)g=(m2+m1+m/2)a (12)
откуда
a = (m2 -m1)g/(m2+m1+m/2) (13)
Отношение масс в правой части формулы (13) есть величина безразмерная. Поэтому числовое значение масс m1, m2, m можно взять в граммах, как они даны в условии задачи. Числовое значение ускорения g надо взять в единицах СИ. После подстановки получим:
а = (200 -100)9,8/(200+100+80/2) = 2,88 м/с2.
2-ой способ. Применим к решению задачи закон сохранения энергии, согласно которому при отсутствии трения полная энергия изолированной системы тел остается неизменной во время движения этих тел: энергия при этом может только превращаться из потенциальной в кинетическую или наоборот. Напомним, что в механике полной энергией тела называется сумма его потенциальной и кинетической энергий.
Положим, что в начальный момент движения потенциальная энергия первого груза была равна П1, второго П2. Через некоторое время высота первого груза увеличилась на h, второго уменьшилась на h (рис.1,б). Потенциальная энергия первого груза стала равна (П1+m1gh), второго (П1-m2gh). Кроме того, каждый из грузов, двигаясь с ускорением а, приобрел за это время скорость v и кинетическую энергию, равную соответственно:
m1v2/2 и m2v2/2. (14)
Точно так же диск, вращаясь равноускоренно, приобрел угловую скорость и соответствующую ей кинетическую энергию:
Ek=I2/2 (15)
Преобразуем выражение кинетической энергии диска. Так как:
I=mr2/2 и =v/r (16)
то
I2/2=1/2(mr2/2)(v2/r2)=mv2/4 (17)
По закону сохранения энергии:
П1+П2 = (П1+m1gh) +(П2-m2gh) +m1v2/2+m2v2/2+mv2/4 (18)
Перенесем члены соответствующие потенциальной энергии грузов, из правой части равенства в левую. После очевидных преобразований получим:
(m2 -m1)gh = (m2+m1+m/2)(v2/2) (19)
Так как грузы двигались равноускоренно, то:
v2 =2gh (20)
Следовательно:
(m2 -m1)g =(m2+m1+m/2)a (21)
откуда
a = (m2 -m1)g/(m2+m1+m/2) (22)
т.е. получен результат, совпадающий с выражением (13).
r
T1'
T1
r
r
T1'
m
T2'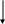
m1g
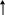

T2
m1
m2
m2g
.
r
m
T1'
T2'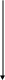
T1
T2
m1g
m2
m1

х
m2g
Контрольная работа № 1.
Вариант |
Номера задач |
||||||||
0 |
2 |
8 |
16 |
22 |
30 |
32 |
36 |
44 |
46 |
1 |
5 |
10 |
19 |
25 |
28 |
31 |
38 |
42 |
48 |
2 |
1 |
13 |
17 |
23 |
26 |
33 |
37 |
43 |
50 |
3 |
3 |
15 |
20 |
24 |
28 |
34 |
40 |
41 |
47 |
4 |
4 |
7 |
18 |
21 |
29 |
35 |
39 |
45 |
49 |
5 |
5 |
12 |
19 |
24 |
27 |
31 |
37 |
44 |
50 |
6 |
2 |
9 |
16 |
22 |
30 |
32 |
36 |
41 |
46 |
7 |
3 |
6 |
18 |
25 |
29 |
33 |
38 |
42 |
48 |
8 |
1 |
11 |
17 |
21 |
26 |
34 |
40 |
45 |
47 |
9 |
4 |
14 |
20 |
23 |
27 |
35 |
39 |
43 |
49 |
Зависимость пройденного телом пути от времени задается уравнением s = A + Bt + Ct2 + Dt3 (C = 0,1 м/с2, D = 0,03 м/с3). Определить: 1) через какое время после начала движения ускорение тела будет равно 2 м/с2; 2) среднее ускорение тела за этот промежуток времени.
Тело, двигаясь с постоянным ускорением, потеряло 2/3 своей начальной скорости. Найти время, за которое это произошло, и путь, пройденный телом за это время.
Материальная точка, двигаясь с постоянным ускорением, проходит расстояние 24 м за 2 с, а следующие 24 м - за 4 с. Найти скорость точки в начале и в конце пути, а также ускорение точки.
С крыши дома высотой 28 м брошен вверх камень со скоростью 8 м/с. Определить скорость падения камня на землю.
Мяч брошен со скоростью 10 м/с под углом 40о к горизонту. На какую высоту поднимется мяч? На каком расстоянии от места бросания он упадет на землю? Какое время он будет в движении?
Тело, брошенное с башни в горизонтальном направлении со скоростью = 20 м/с, упало на землю на расстоянии s (от основания башни), вдвое больше высоты h башни. Найти высоту башни.
Колесо радиуса R = 0,1 м вращается так, что зависимость угловой скорости от времени задается уравнением = 2At + 5Bt4 (А = 2 рад/с2 и В = 1 рад/с5). Определить полное ускорение точек обода колеса через t =1с после начала вращения и число оборотов, сделанных колесом за это время.
Маховик начал вращаться равноускоренно и за промежуток времени 10 с достиг частоты вращения 300 об/мин. Определить угловое ускорение маховика и число оборотов, которое он сделал за это время.
Вентилятор вращается с частотой 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75 об. Какое время прошло с момента выключения вентилятора до полной его остановки?
Найти радиус вращающегося колеса, если известно, что линейная скорость точки, лежащей на ободе, в 2,5 раза больше линейной скорости точки, лежащей на 5 см ближе к оси колеса.
Чему равна линейная скорость на ободе турбины диаметром 9 м, если частота вращения 1,2 Гц? На каком расстоянии от оси линейная скорость равна 15 м/с?
Колесо вращается с угловым ускорением 2 рад/с2. Через время t = 0,5 с после начала движения полное ускорение колеса а = 13,6 см/с2. Найти радиус колеса.
Канат лежит на столе так, что часть его свешивается со стола, и начинает скользить тогда, когда длина свешивающейся части составляет 1/4 его длины. Найти коэффициент трения каната о стол.
К концам нити, перекинутой через блок, подвешены два тела массами 200 г и 150 г. Определить, за какое время тела пройдут расстояние 1 м.
Тело весом 20 Н скользит по горизонтальной поверхности под действием груза весом 5 Н, прикрепленного к концу шнура, привязанного к телу и перекинутого через неподвижный блок. С каким ускорением движется тело и какова сила натяжения шнура? Коэффициент трения равен 0,1.
На наклонной плоскости находится тело весом Р = 500 Н, на которое действует горизонтально направленная сила F = 300 Н. Определить ускорение тела и силу, с которой оно давит на плоскость. Наклонная плоскость составляет с горизонтом угол 30о. Трение не учитывать.
Наклонная плоскость, образующая угол 25о с плоскостью горизонта, имеет длину 2 м. Тело, двигаясь равноускоренно, соскользнуло с этой плоскости за время 2 с. Определить коэффициент трения о плоскость.
Блок укреплен на вершине двух наклонных плоскостей, составляющих с горизонтом углы 30о и 45о. Гири равной массы (m = 2 кг) соединены нитью, перекинутой через блок. Блок и нити невесомы. Коэффициенты трения гирь о плоскость f = 0,1. Определить ускорение, с которым движутся гири и силу натяжения нити.
Пуля массой m = 10 г, летевшая горизонтально со скоростью = 500 м/с, попадает в баллистический маятник длиной l = 1 м и массой M = 5 кг и застревает в нем. Определить угол отклонения маятника.
Шар массой 200 г, движущийся со скоростью 10 м/с, ударяет неподвижный шар массой 800 г. Удар прямой, абсолютной упругий. Каковы будут скорости шаров после удара?
Два груза массами m = 10 кг и M = 15 кг подвешены на нитях длиной l = 2 м так, что грузы соприкасаются между собой. Меньший груз был отклонен на угол 60о и отпущен. На какую высоту h поднимутся оба груза после неупругого удара? Какое количество теплоты при этом выделится?
Шар массой 2 кг, движущийся со скоростью 1,2 м/с, налетает на покоящийся шар массой 1,5 кг. Вычислить скорости шаров после упругого взаимодействия.
Камень массой 500 г, брошенный под углом к горизонтальной плоскости, через 4 секунды упал на нее обратно на расстоянии 16 м. Найти работу бросания.
При подъеме груза массой 2 кг на высоту 1 м сила F совершает работу 78,5 Дж. С каким ускорением поднимается груз?
Шар массой 3 кг движется со скоростью 4 м/с и ударяется о неподвижный шар такой же массы. Считая удар центральным и абсолютно неупругим, найти количество теплоты, выделившееся при ударе.
Горизонтальная платформа массой 120 кг вращается с частотой 6 об/мин. Человек массой 80 кг стоит на краю платформы. С какой частотой начнет вращаться платформа, если человек перейдет в ее центр? Платформу принять за однородный диск.
Диск массой 5 кг вращается с частотой 5 Гц. Определить работу, которую надо совершить, чтобы частота вращения увеличилась в 3 раза. Радиус диска равен 20 см.
На барабан массой М = 9 кг намотан шнур, к концу которого привязан груз массой m = 2 кг. Найти ускорение груза. Барабан считать однородным цилиндром.
Вал в виде сплошного цилиндра массой 10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой 2 кг. С каким ускорением будет опускаться гиря, если ее предоставить самой себе?
К ободу однородного сплошного диска радиусом R = 0,5 м приложена постоянная касательная сила F = 100 Н. При вращении диска на него действует момент сил трения М = 2 Нм. Определить массу m диска, если известно, что его угловое ускорение постоянно и равно 12 рад/с2.
Через какое время от начала движения точка, совершающая гармоническое колебание, сместится от положения равновесия на половину амплитуды? Период колебаний Т = 24 с, начальная фаза равна нулю.
Диск радиусом 24 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Определить приведенную длину и период колебаний такого маятника.
Начальная фаза гармонического колебания равна нулю. Через какую долю периода скорость точки будет равна половине ее максимальной скорости?
Медный шарик, подвешенный к пружине, совершает вертикальные колебания. Как изменится период колебаний, если к пружине подвесить вместо медного шарика алюминиевый такого же радиуса?
Амплитуда гармонических колебаний материальной точки 2 см, полная энергия колебаний 0,3 мкДж. При каком смещении от положения равновесия на колеблющуюся точку действует сила 22,5 мкДж?
Максимальная скорость колебаний точки равна 10 м/с, амплитуда колебаний - 2 мм. Определить максимальное ускорение точки.
На железнодорожной платформе установлено орудие. Масса платформы с орудием 15 т. Орудие стреляет вверх под углом 60о к горизонту в направлении пути. С какой скоростью покатится платформа вследствие отдачи, если масса снаряда 20 кг и он вылетает со скоростью 600 м/с?
Грузик, привязанный к шнуру длиной 50 см, описывает окружность в горизонтальной плоскости. Какой угол образует шнур с вертикалью, если частота вращения 1 с-1?
Автомобиль идет по закруглению шоссе, радиус кривизны которого равен 200 м. Коэффициент трения колес о покрытие дороги равен 0,1. При какой скорости автомобиля начнется его занос?
Грузик, привязанный к нити длиной 1 м, описывает окружность в горизонтальной плоскости. Определить период обращения, если нить наклонена на угол 60о от вертикали.
Два неупругих шара массами 2 кг и 3 кг движутся со скоростями соответственно 8 м/с и 4 м/с. Определить увеличение внутренней энергии шаров при их столкновении в двух случаях: меньший шар нагоняет больший; шары движутся навстречу друг другу.
Из двух соударяющихся абсолютно упругих шаров большой шар покоится. В результате прямого удара меньший шар потерял 3/4 своей кинетической энергии. Определить отношение масс шаров.
Определить момент инерции тонкого однородного стержня длиной 30 см и массой 100 г относительно оси, перпендикулярной стержню и проходящей через: его конец; его середину; точку, отстоящую от конца стержня на 1/3 его длины.
Найти момент инерции тонкого однородного кольца радиусом 20 см и массой 100 г относительно оси, лежащей в плоскости кольца и проходящей через его центр.
Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязали грузики массой 100 г и 110 г. С каким ускорением будут двигаться грузики, если масса блока 400 г?
Через неподвижный блок массой 0,2 кг перекинут шнур, к концам которого подвесили грузы массами 0,3 кг и 0,5 кг. Определить силы натяжения шнура по обе стороны блока во время движения грузов, если масса блока равномерно распределена по ободу.
Определить жесткость системы двух пружин при последовательном и параллельном их соединении. Жесткость пружин 2 кН/м и 6 кН/м.
К стальному стержню длиной 3 м и диаметром 2 см подвешен груз массой 2,5103 кг. Определить напряжение в стержне, относительное и абсолютное удлинение стержня.
Гиря, положенная на верхний конец спиральной пружины, поставленной на подставке, сжимает ее на 2 мм. На сколько сожмет пружину та же гиря, упавшая на конец пружины с высоты 5 см?
Стальной стержень длиной 2 м и площадью поперечного сечения 2 см2 растягивается силой 10 кН. Найти потенциальную энергию растянутого стержня и объемную плотность энергии.
