4. Вплив зростання населення на капіталоозброєність

Ця функція означає, що під впливом технологічного прогресу у

співвідношенні капітал — праця змінюється праця

Технологічний прогрес викликає приріст ефективності праці Е з темпом g.

Це означає, що випуск продукції на одного працівника також зростає з

темпом g.

Тепер формули для визначення капіталоозброєності та продуктивності

набувають такого вигляду:

де А: — капітал на одиницю праці з постійною ефективністю, у — обсяг

виробництва на одиницю праці з постійною ефективністю.

Рівняння зміни капіталоозброєності має вигляд

Приріст запасів капіталу із зростанням технологічного прогресу

знизиться.

Отже, якщо населення зростає з темпом п, а ефективність праці — з темпом

g, то загальний обсяг виробництва збільшується під впливом приросту

населення та технологічного прогресу з темпом (п + g).

З урахуванням технологічного прогресу "золоте правило" формулюється

таким чином: для максимізації споживання необхідно, щоб гранична

продуктивність капіталу (приріст продукту на додаткову одиницю капіталу

без амортизації) дорівнювала темпові приросту загального обсягу

виробництва (п + g):

Модель Солоу показує, що зростання заощаджень у короткостроковому

періоді веде до збільшення капітальних запасів та обсягу виробництва. Це

відбувається лише до моменту досягнення рівноважного стану економіки при

стійкому рівні капіталоозброєності. У довгостроковому періоді зростання

виробництва залежить від темпу технологічного прогресу

Розглянемо більш детально неокласичну модель економічного зростання Р. Солоу

Неокласичні моделі зростання долали ряд обмежень кейнсіанських моделей і дозволяли більш точно описати особливості макроекономічних процесів. Р. Солоу показав, що нестабільність динамічної рівноваги в кейнсіанських моделях була наслідком невзаємозамінні факторів виробництва. Замість функції Леонтьєва він використовував у своїй моделі виробничу функцію Кобба-Дугласа, в якій праця і капітал є субститутами. Іншими передумовами аналізу в моделі Солоу є: спадна гранична продуктивність капіталу, постійна віддача від масштабу, постійна норма вибуття, відсутність інвестиційних лагів.

Взаємозамінність факторів (зміна капіталовооруженності) пояснюється не тільки технологічними умовами, але і неокласичної передумовою про досконалої конкуренції на ринках факторів.

Необхідною умовою рівноваги економічної системи є рівність сукупного попиту та пропозиції. Пропозиція описується виробничою функцією з постійною віддачею від масштабу: Y = F (K, L) і для будь-якого позитивного z вірно: zF (K, L) = F (zK, zL). Тоді якщо z = 1 / L, тоY / L = F (K / L, 1). Позначимо (Y / L) через у, а (K / L) через к і перепишемо вихідну функцію в формі взаємозв'язку між продуктивністю і фондоозброєністю (капіталоозброєності): у = ƒ (k) (див. рис. 1). Тангенс утла нахилу даної виробничої функції відповідає граничному продукту капіталу (МРК), який зменшується в міру зростання фондоозброєності (k).

остю.

Розглянемо більш детально неокласичну модель економічного зростання Р. Солоу.

Рис.1

Сукупний попит в моделі Солоу визначається інвестиціями та споживанням: у = i + с, де i і с - інвестиції і споживання в розрахунку на одного зайнятого. Дохід ділиться між споживанням і заощадженнями відповідно до норми заощадження, так що споживання можна представити як з = (1-s) y, де s-норма заощадження (накопичення), тоді у = с + i = (1-s) y + i,

звідки i = sy. В умовах рівноваги інвестиції дорівнюють заощадженням і пропорційні доходу.

Умови рівності попиту і пропозиції можуть бути представлені як ƒ (k) = з + i або ƒ (k) = i / s. Виробнича функція визначає пропозицію на ринку товарів, а нагромадження капіталу - попит на вироблений продукт.

Динаміка обсягу випуску залежить від обсягу капіталу (у нашому випадку-капіталу в розрахунку на одного зайнятого, або капіталовооруженності). Обсяг капіталу змінюється під впливом інвестицій та вибуття: інвестиції збільшують запас капіталу, вибуття - зменшує.

Інвестиції залежать від фондоозброєності і норми накопичення, що випливає з умови рівності попиту і пропозиції в економіці: i = sƒ (k). Норма накопичення визначає поділ продукту на інвестиції та споживання при будь-якому значенні k (рис. 1): у = ƒ (k), i = sƒ (k), с = (1-s) ƒ (k).

Амортизація враховується таким чином: якщо прия, що щорічно внаслідок зносу капіталу вибуває його фіксована частина d (норма вибуття), то величина вибуття буде пропорційна обсягу капіталу і дорівнює dk. На графіку цей зв'язок відображається прямий, що виходить з точки початку координат, з кутовим коефіцієнтом d (рис. 2).

Вплив інвестицій та вибуття на динаміку запасів капіталу можна представити рівнянням: Δk = i-dk, або, використовуючи рівність інвестицій і заощаджень, Δk = sƒ (k)-dk. Запас капіталу (k) буде збільшуватися (Δk> 0) до рівня, при якому інвестиції будуть дорівнюють величині вибуття, тобто sƒ (k) = dk. Після цього запас капіталу на одного зайнятого (фондоозброєність) не буде змінюватися в часі, оскільки дві діючі на нього сили урівноважать один одного (Δk = 0). Рівень запасу капіталу, при якому інвестиції дорівнюють вибуття, називається рівноважним (стійким) рівнем фондоозброєності праці і позначається k *. При досягненні k * економіка знаходиться в стані довгострокової рівноваги.

Рис.2

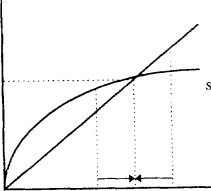
Рівновага є стійким, оскільки незалежно від початкового значення до економіка буде прагнути до рівноважного стану, тобто до k *. Якщо початкове k1 нижче k *, то валові інвестиції (sƒ (k) будуть більше вибуття (dk) і запас капіталу буде зростати на величину чистих інвестицій. Якщо k2> k *, це означає, що інвестиції менше, ніж знос, а значить запас капіталу буде скорочуватися, наближаючись до рівня k * (див. рис. 2).

Норма накопичення (заощадження) безпосередньо впливає на стійкий рівень фондоозброєності. Зростання норми заощадження з s1 до s2 зрушує криву інвестицій вгору з положення s1ƒ (k) до s2 (k) (див. рис. 3).

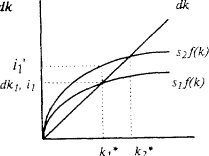
Рис.3

У вихідному стані економіка мала стійкий запас катала k1 *, при якому інвестиції дорівнювали вибуття. Після підвищення норми заощадження інвестиції зросли на (i'1-i1), а запас капіталу (k1 *) і вибуття (dk1) залишилися колишніми. У цих умовах інвестиції починають перевищувати вибуття, що викликає зростання запасу капіталу до рівня нової рівноваги k2 *, що характеризується більш високими знаннями фондоозброєності і продуктивності праці (випуск на одного зайнятого, у).

Таким чином, чим вище норма заощадження (накопичення), тим вищий рівень випуску та запасу капіталу може бути досягнутий в стані стійкої рівноваги. Однак підвищення норми накопичення веде до прискорення економічного зростання в короткостроковому періоді, до тих пір, поки економіка не досягне точки нової стійкої рівноваги.

Очевидно, що ні сам процес накопичення, ні збільшення норми заощадження не можуть пояснити механізм безперервного економічного зростання. Вони показують лише перехід від одного стану рівноваги до іншого.

Для подальшого розвитку моделі Солоу черзі знімаються дві передумови: незмінність чисельності населення і його зайнятої частини (їх динаміка передбачається однаковою) і відсутність технічного прогресу.

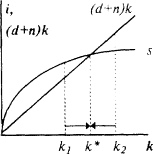
Припустимо, населення зростає з постійним темпом n. Це новий чинник, що впливає разом з інвестиціями і вибуттям на фондоозброєність. Тепер рівняння, що показує зміна запасу капіталу на одного працівника, буде виглядати як: Δk = i-dk-nk або Δk = i-(d + n) k.

Зростання населення аналогічно вибуття знижує фондоозброєність, хоча і по-іншому - не через зменшення наявного запасу капіталу, а шляхом розподілу його між зростанням числа зайнятих. У даних умовах необхідний такий обсяг інвестицій, який не тільки б покрив вибуття капіталу, але і дозволив би забезпечити капіталом нових робочих в колишньому обсязі. Твір nk показує, скільки потрібно додаткового капіталу в розрахунку на одного зайнятого, щоб капіталовооруженность нових робочих була на тому ж рівні, що і старих

Рис. 4 Рис. 5

k k′* k′

(капітал на ефективну одиницю праці)

Умова стійкої рівноваги в економіці при незмінній фондоозброєнності k * можна буде записати тепер так:

Δk = sƒ (k) - (d + n) k = 0 або sƒ (k) = (d + n) k

Даний стан характеризується повною зайнятістю ресурсів (рис. 4).

У стійкому стані економіки капітал і випуск на одного зайнятого, тобто фондоозброєність (k) і продуктивність (у) праці залишаються незмінними. Але, щоб фондоозброєність залишалася постійною і при зростанні населення, капітал повинен зростати з тим же темпом, що і населення, тобто:

ΔY / Y = ΔL / L = ΔK / K = n.

Таким чином, зростання населення стає однією з причин безперервного економічного зростання в умовах рівноваги.

Зазначимо, що зі збільшенням темпу росту населення зростає кутовий коефіцієнт кривої (d + n) k, що призводить до зменшення рівноважного рівня фондоозброєності (k '*), отже, до падіння у.

Облік у моделі Солоу технологічного прогресу видозмінює вихідну виробничу функцію. Передбачається трудосберегающий форма технологічного прогресу, Виробнича функція буде представлена ​​як Y = F (K, LE), де E-ефективність праці, а LE - чисельність умовних одиниць праці з постійною ефективністю Е. Чим вище Е, тим більше продукції може бути вироблено даними числом працівників. Пропонується, що технологічний прогрес здійснюється шляхом зростання ефективності праці Е з постійним темпом g. Зростання ефективності праці в даному випадку аналогічний за результатами зростанню чисельності зайнятих: якщо технологічний прогрес має темп g = 2%, то, наприклад, 100 робітників можуть зробити стільки ж продукції, скільки раніше виробляли 102 робітників. Якщо тепер чисельність зайнятих (L) зростає з темпом n, а Е зростає з темпом g, то (LЕ) буде збільшуватися з темпом (n + g).

Включення технологічного прогресу дещо змінює і аналіз стану стійкої рівноваги, хоча хід міркувань зберігається. Якщо визначити k 'як кількість капіталу в розрахунку на одиницю праці з постійною ефективністю, тобто k '= K / LE, а y' = Y / LE, то результати зростання ефективних одиниць праці аналогічні зростанню чисельності зайнятих (збільшення кількості одиниць праці з постійною ефективністю знижує величину капіталу, що припадає на одну таку одиницю). У стані стійкої рівноваги (рис. 5) рівень фондоозброєності k '* врівноважує, з одного боку, вплив інвестицій, що підвищують фондоозброєність, а, з іншого боку, вплив вибуття, зростання числа зайнятих і технологічного прогресу, що знижують рівень капіталу в розрахунку на ефективну одиницю праці: sƒ (k ') = (d + n + g) k'.

У стійкому стані (k '*) при наявності технологічного прогресу загальний обсяг капіталу (К) і випуску (У), будуть рости з темпом (n + g). Але на відміну від випадку зростання населення, тепер будуть рости з темпом g фондоозброєність (K / L) і випуск (Y / L) в розрахунку на одного зайнятого; останнє може служити основою для підвищення добробуту населення. Технологічний прогрес у моделі Солоу є, отже, єдиною умовою безперервного зростання рівня життя, оскільки лише за його наявності спостерігається стійке зростання випуску на душу населення (у).

Таким чином в моделі Солоу знайдено пояснення механізму безперервного економічного зростання в режимі рівноваги при повній зайнятості ресурсів.

Як відомо, в кейнсіанських моделях норма заощадження задавалася екзогенно і визначала величину рівноважного темпу зростання доходу. У неокласичній моделі Солоу при будь-якій нормі заощадження ринкова економіка прагне до відповідного стійкого рівня фондоозброєності (k *) і збалансованого зростання, коли дохід і капітал зростають з темпом (n + g). Величина норми заощадження (накопичення) є об'єктом економічної політики і важлива при оцінці різних програм економічного зростання.

Оскільки рівноважне економічне зростання сумісний з різними нормами заощадження (як ми бачили, збільшення s лише на короткий час прискорювало зростання економіки, в тривалому періоді економіка поверталася до сталого рівноваги і постійного темпу зростання в залежності від значення n і g), виникає проблема вибору оптимальної норми заощадження.

Оптимальна норма нагромадження, відповідна "золотому правилу" Е. Фелпса, забезпечує рівноважне економічне зростання з максимальним рівнем споживання. Стійкий рівень фондоозброєності, що відповідає цій нормі накопичення, позначимо k **, а споживання - з **.

Рівень споживання в розрахунку на одного зайнятого при будь-якому стійкому значенні фондоозброєнності k * визначається шляхом ряду перетворень вихідного тотожності: у = с + i. Висловлюємо споживання с через у і i і підставляємо значення цих параметрів, які вони приймають в стійкому стані: з = у-i, з *= ƒ (k *)-dk *, де з * - споживання в стані стійкого зростання, а i = sƒ (k) = dk за визначенням сталого рівня фондоозброєності. Тепер з різних стійких рівнів фондоозброєнності (k *), відповідних різним значенням s, необхідно вибрати такий, при якому споживання досягає максимуму (рис. 6).

Рис.6

Якщо вибрано k * <k **, то обсяг випуску збільшується у більшій мірі, ніж величина вибуття (лінія ƒ (k *) на графіку крутіше, ніж dk *), а значить різниця між ними, що дорівнює споживанню, зростає. При k *> k ** збільшення обсягу випуску менше зростання вибуття, тобто споживання падає. Зростання споживання можливий лише до точки k **, де воно досягає максимуму (виробнича функція і крива dk * мають тут однаковий нахил). У цій точці збільшення запасу капіталу на одиницю дасть приріст випуску, рівний граничному продукту капіталу (МРК), і збільшить вибуття на величину d (знос на одиницю капіталу). Зростання споживання не буде, якщо весь приріст випуску буде використаний на збільшення інвестицій для покриття вибуття. Таким чином, при рівні фондоозброєності, відповідному "золотому правилу" (k **), повинна виконуватися умова: МРК = d (граничний продукт капіталу дорівнює нормі вибуття), а з урахуванням зростання населення та технологічного прогресу: МРК = d + n + g .

Якщо економіка в початковому стані має запас капіталу більший, ніж слід по "золотому правилу", необхідна програма зі зниження норми накопичення. Ця програма обумовлює збільшення споживання та зниження інвестицій. При цьому економіка виходить зі стану рівноваги і знову досягає його при пропорціях, що відповідають "золотому правилу".

Якщо економіка в початковому стані має запас капіталу менше, ніж k **, необхідна програма, спрямована на підвищення норми заощадження. Ця програма спочатку призводить до зростання інвестицій та падіння споживання, але в міру накопичення капіталу з певного моменту споживання знову починає рости. У результаті економіка досягає нової рівноваги, але вже відповідно до "золотим правилом", де споживання перевищує вихідний рівень. Дана програма зазвичай вважається непопулярною у зв'язку з наявністю "перехідного періоду", що характеризується падінням споживання, тому її прийняття залежить від межчасовий переваг політиків, їх орієнтації на короткостроковий або довгостроковий результат.

Розглянута модель Солоу дозволяє описати механізм довгострокового економічного зростання, зберігає рівновагу в економіці і повну зайнятість факторів. Вона виділяє технічний прогрес як єдину основу сталого зростання добробуту і дозволяє знайти оптимальний варіант зростання, що забезпечує максимум споживання.

Представлена ​​модель не вільна і від недоліків. Модель аналізує стану стійкої рівноваги, що досягаються в тривалій перспективі, тоді як для економічної політики важлива і короткострокова динаміка виробництва і рівня життя. Багато екзогенні змінні моделі Солоу - s, d, n, g - було б краще визначати всередині моделі, оскільки вони тісно пов'язані з іншими її параметрами і можуть видозмінювати кінцевий результат. Модель не включає також цілий ряд обмежувачів зростання, суттєвих в сучасних умовах - ресурсних, екологічних, соціальних. Використовувана в моделі функція Кобба-Дугласа, описуючи лише певний тип взаємодії факторів виробництва, не завжди відображає реальну ситуацію в економіці. Ці та інші недоліки намагаються подолати сучасні теорії економічного зростання.

У неокласичній моделі зростання обсяг випуску в стійкому стані росте з темпом (n + g), а випуск на душу населення - з темпом g, тобто стійкий темп зростання визначається екзогенно. Сучасні теорії ендогенного зростання намагаються визначити стійкий темп зростання в рамках моделі, ендогенно, пов'язуючи його з усіма можливими кількісними та якісними чинниками: ресурсними, інституційними та ін

Прихильники концепції "економіки пропозиції" вважають, що збільшення темпів росту при повній зайнятості, насамперед, можливо шляхом скорочення регулюючого втручання ззовні в ринкову систему.