
- •8.1. Механический принцип относительности. Преобразования Галилея.
- •8.3. Преобразования Лоренца.
- •Пустьдана §. Найдём . Из преобразованияифференцирования получим embed Equation.2uation.2 µ §. В векторной форме
- •4). Релятивистская энергия.
- •5). Связь энергии с импульсом.
- •6). Законы сохранения энергии и импульса для замкнутых систем.
Пустьдана §. Найдём . Из преобразованияифференцирования получим embed Equation.2uation.2 µ §. В векторной форме
EMBED Eзàêон преобразования скоростей.
Следует:
1).
Если
äвижется
одно и торость
в разных ИСО рation.2
µ §,
гдеительная,
![]() -
переносная
скорости. При
-
переносная
скорости. При
![]() <<
1 получаем ньютоновское сложение
скоростей, т.е.
<<
1 получаем ньютоновское сложение
скоростей, т.е.
![]() =
+
.
=
+
.
2). Закон удовлетворяет
принципу постоянства скорости света.
Пусть U
= c,
тогда
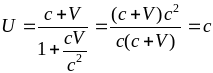 .
.
3). При сложении двух скоростей сколь угодно близких к скорости света, результирующая скорость всегда будет меньше неё.
 , т.е.
U
<
c
, т.е.
U
<
c
![]() .
.
Элементы релятивистской динамики.
Закон Ньютона в
форме
![]() -
инвариантен к преобразованиям Галилея,
но неинвариантен к преобразованиям
Лоренца. Если представить
-
инвариантен к преобразованиям Галилея,
но неинвариантен к преобразованиям
Лоренца. Если представить
![]() ,
где
,
где
![]() - скорость
тела в избранной ИСО, m0
- масса покоя тела (инвариантная величина),
c
- скорость света, то
- скорость
тела в избранной ИСО, m0
- масса покоя тела (инвариантная величина),
c
- скорость света, то
 -
закон Ньютона становится инвариантным
к преобразованиям Лоренца.
-
закон Ньютона становится инвариантным
к преобразованиям Лоренца.
Анализ:
1). При переходе от
одной ИСО к другой должны соответствующим
образом преобразовываться компоненты
![]() и изменяться масса тела.
и изменяться масса тела.
2).
 .
Интегрируем это выражение и получаем
.
Интегрируем это выражение и получаем
![]() ,
где G
- постоянная.
,
где G
- постоянная.
Если при t
= 0, U
= 0, то G
= 0. Решаем уравнение
![]() относительно U
.
относительно U
.
 или m02
U
2 c
2 = F
2
t
2
c2
-
F
2 t
2U
2.
Отсюда
или m02
U
2 c
2 = F
2
t
2
c2
-
F
2 t
2U
2.
Отсюда
U
2(m02
c
2 + F
2
t
2
) = F
2
t
2
c2.
Окончательно
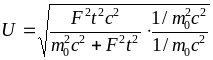 или
или
 .
.
I - релятивистская скорость, которая медленно нарастает, но U < c.
II - ньютоновская
скорость, получается при F
/ m0
t
<< c
, т.е.
![]() .
Область А - область ньютоновской механики.
.
Область А - область ньютоновской механики.
![]() - релятивистский импульс.
В классической механике
- релятивистский импульс.
В классической механике
![]() ,
т.е. когда U
2
/
c
2
=
2
<< 1 .
Величина
,
т.е. когда U
2
/
c
2
=
2
<< 1 .
Величина
![]() - называется релятивистской
массой, тогда
релятивистский импульс
- называется релятивистской
массой, тогда
релятивистский импульс
![]() .
.
При U 0 1/ c2 б/м, тогда m m0.
При U
c
![]() б/м,
тогда m
.
б/м,
тогда m
.
Величина m0 - инвариантная величина одинаковая для всех ИСО. Как и в ньютоновской механике масса является мерой инерции тела. Физически факт m при U c можно объяснить тем, что дальнейшее увеличение просто невозможно, т.е. скорость света недостижима.
При разложении
![]()

получаем m
=
m0
(1 +
1/2
2
)
,
т.е.
релятивистская масса состоит из двух
частей: m0-
масса покоя
и mдв
= m0
/2
2
-
масса движения,
которая
является функцией кинетической энергии
тела,
т.к.
![]() ,
делённая
на c2
.
Частицы с
m0
= 0
всегда движутся с U
= c.
При U
< c
они не существуют.
У частиц
с m0
>
0 U
должна быть <
c
.
,
делённая
на c2
.
Частицы с
m0
= 0
всегда движутся с U
= c.
При U
< c
они не существуют.
У частиц
с m0
>
0 U
должна быть <
c
.
4). Релятивистская энергия.
Из определения
работы
 ,
тогда
,
тогда
 .
Преобразуем
.
Преобразуем
 =
=
 .
.
После интегрирования
W(E)
=
![]() +
Const .
Константа
в данном выражении была найдена
Эйнштейном,
причём она оказалась равной нулю.
Окончательно получаем W(E)
=
=
mc2,
где m
=
+
Const .
Константа
в данном выражении была найдена
Эйнштейном,
причём она оказалась равной нулю.
Окончательно получаем W(E)
=
=
mc2,
где m
=
![]() .
.
Анализ:
а). E = mc2 - это закон взаимосвязи массы и энергии тела. Эквивалентность этих величин справедлива для любого вида энергии.
б).
Пусть U
= 0,
т.е. тело
покоится,
тогда
![]() и
E
=
m0c2
=
E0.
Получили
энергию покоя не связанную с движением
тела.
Это энергия,
связанная с веществом и при определённых
условиях,
может
перейти в электромагнитное излучение.
и
E
=
m0c2
=
E0.
Получили
энергию покоя не связанную с движением
тела.
Это энергия,
связанная с веществом и при определённых
условиях,
может
перейти в электромагнитное излучение.
T =
m0c2
(![]() )
или
)
или
T
= mc2
-
m0c2
.
При U
<< c
T
=
![]() .
Область А
- область ньютоновской механики.
.
Область А
- область ньютоновской механики.
г). Закон сохранения энергии можно сформулировать в виде закона сохранения массы, так как каждой массе (или изменению массы) соответствует определённая энергия (изменение энергии): E ~ m.
