кр по вышке № 4вариант 1

Контрольная работа № 4

Задачи 121-130. Вычислить: 1-3) производную ; 4) производные ; 5) в данной точке ; 6) производную n-го порядка для данной функции y(x).

121. 1) ; 2) 3) 4) ;

5) ; 6)

Решение:

1) 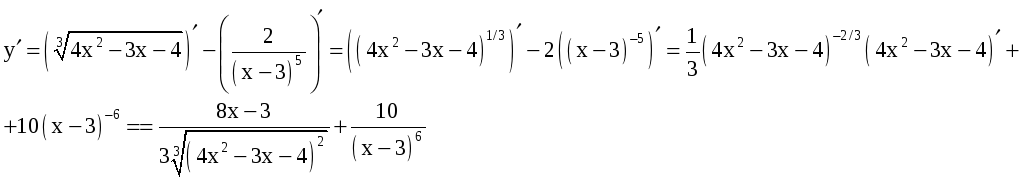2) Используя правило дифференцирования сложной функции, получим

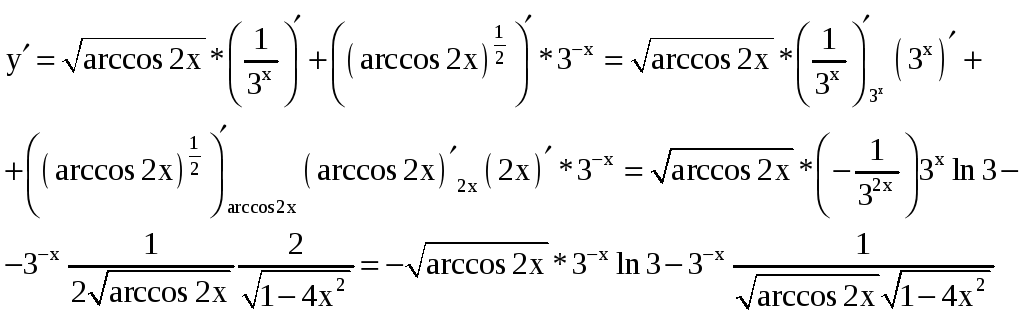
3) Применим правило дифференцирования

[ f(x)^g(x) ]^ = g(x) ·f(x)^{g(x)  1} ·f^ (x) + f(x)^g(x) ·lnf(x) ·g^ (x), а также правило дифференцирования сложной функции:

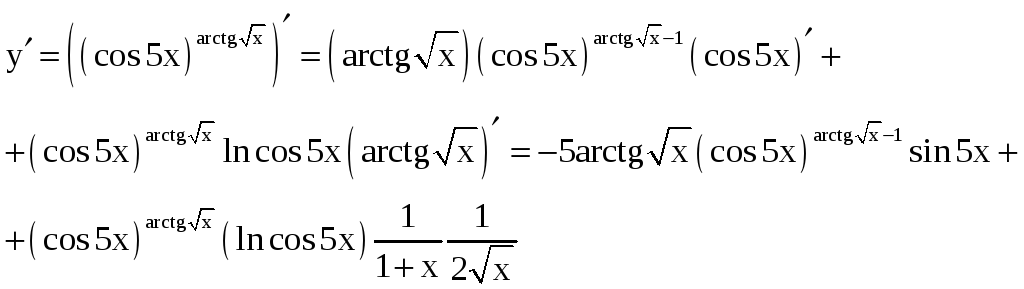
4) Поскольку функция задана неявно, ее следует продифференцировать по x, считая у функцией от х . . Далее, аналогичным образом найдем вторую производную:

То есть, учитывая что первая производная равна , получим .

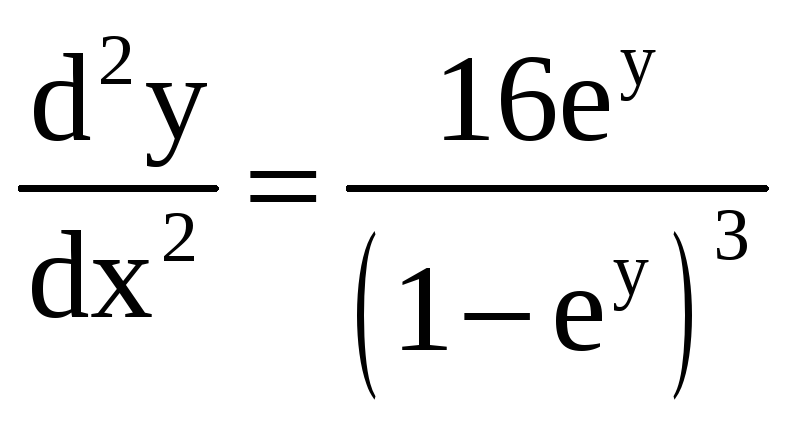5)

6) Найдем первую производную:

— производная второго порядка;

— производная третьего порядка и т.д. Следовательно, производная n-го порядка для данной функции будет иметь вид

Задачи 131-140. Применяя формулу Тейлора с остаточным членом в форме Лагранжа, вычислить значение функции с точностью до 0,001.

131. .

Решение: Выражение представимо в виде при x=64. В частности, при x₀=63 .

Для вычисления значения функции применим формулу Тейлора:

f(x) = f(x₀ ) + f^ (x₀ ) (x  x₀ )/ 1!+ f^" (x₀ ) (x  x₀ )²/2! + ... + f⁽ⁿ⁾ (x₀ ) (x  x₀ )ⁿ/ n! + R_n (x), где . Требование будет выполнено, если

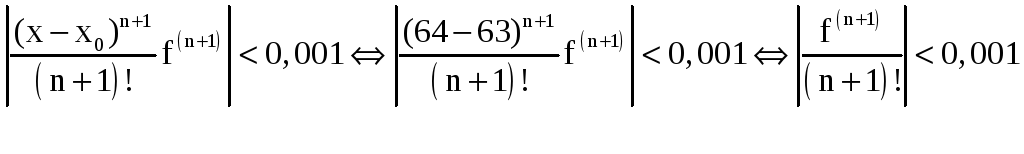
Найдем первую производную при 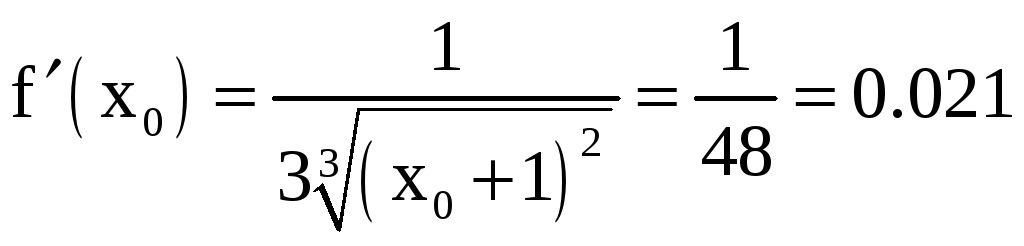n=0 . При n=0 . Найдем вторую производную при n=1 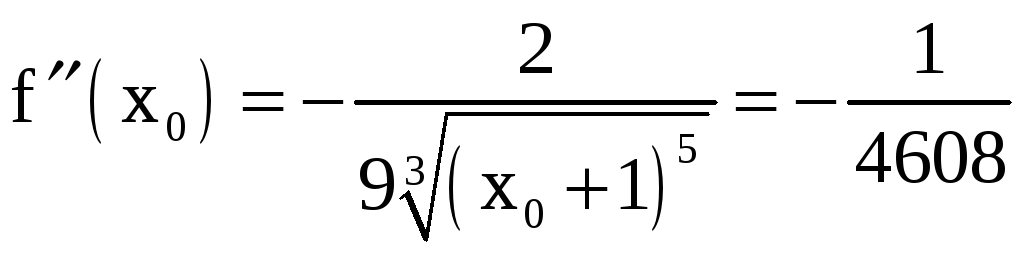Это удовлетворяет заданной точности, поскольку 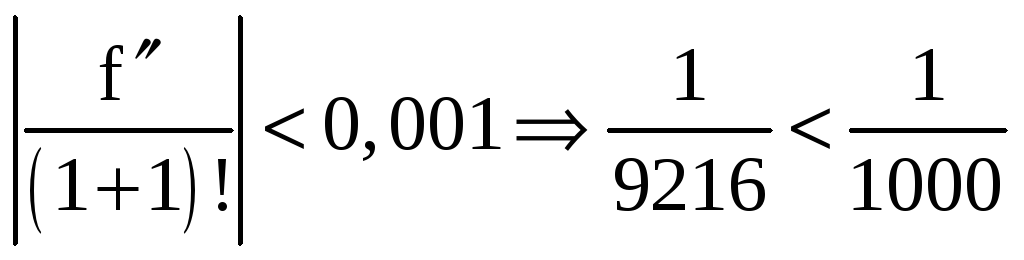. Отсюда находим значение функции при n=1 в ряде Тейлора:

Ответ:

Задачи 141-150. Найти наибольшее и наименьшее значения функции y=f(x) на отрезке [a;b].

141. .

Решение:

Найдем производную . y`=0 при x=1— это единственная критическая точка на . Вычисляем значения функции на концах отрезка и в критической точке:

Ответ: при x=1; y_max=ln5 при x=3.

Задачи 151-160. Провести полное исследование данной функции и построить ее график.

151.

Решение:

1) Область определения функции Область допустимых значений функции y>0.

2) Функция не является четной или нечетной.

3) График функции не пересекает ось OX, так как уравнение не имеет действительных корней. Найдем точки пересечения графика с осью ОY; имеем y=e⁰=1 при x=0.

4) Найдем производную: . Существует единственная критическая точка x=1. В промежутке , следовательно, функция возрастает; в промежутке , следовательно, функция убывает. Значит, при x=1— в точке максимума — y_max=e¹=е=2.718.

5) Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба. Так как

.

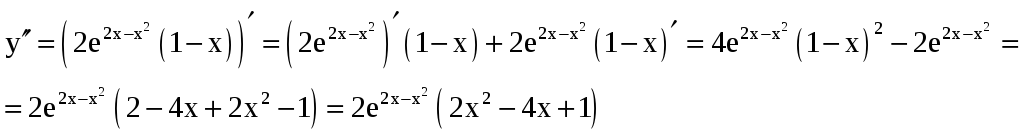Корни уравнения равны — точки перегиба, значит, на интервалах и функция выпукла вниз; на интервале и функция выпукла вверх.

6) График функции не имеет вертикальной асимптоты, так как ни одно из предельных значений не является бесконечным: . Найдем наклонные асимптоты:

Следовательно, наклонная асимптота имеет уравнение y=0.

Строим график функции.

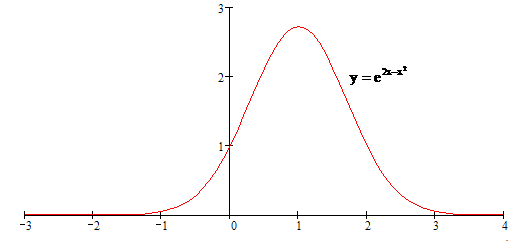
Задачи 161-170.

161. Полотняный шатер объемом V имеет форму прямого конуса. Каково должно быть отношение высоты конуса к радиусу его основания, чтобы на шатер пошло наименьшее количество полотна?

Решение:

Обозначим радиус основания через y, а высоту через x. Тогда объем шатра , отсюда . Площадь боковой поверхности шатра . Исследуем полученную функцию на минимум на промежутке : 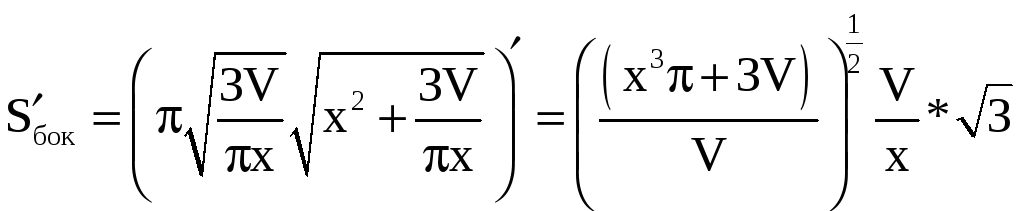. , если . Найдем отношение высоты конуса к радиусу его основания .

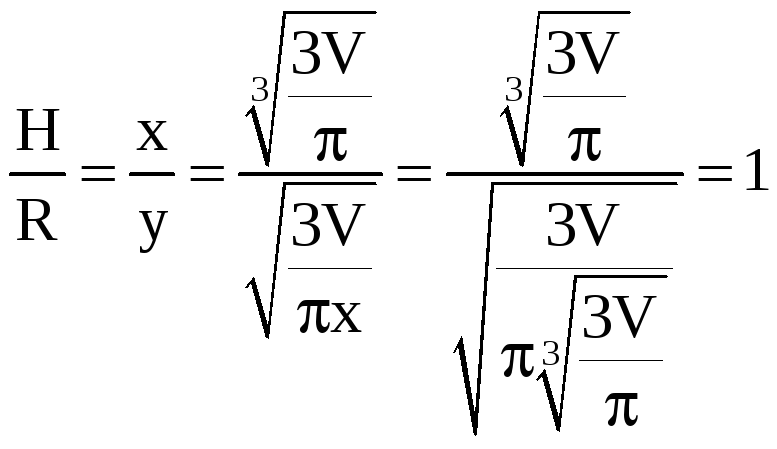Ответ: 1.