Контрольные работы №№7,8 вар. 3 По теме Ряды по ВМ

Министерство образования Республики Беларусь

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

“БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ”

КОНТРОЛЬНАЯ РАБОТА № 7, №8

по высшей математике (ч. 4)

(вариант №3)

студента

ФЗО, специальность ИСИТвЭ,

Номер ЗК .

Домашний адрес:

конт. тел.

Минск, 2009

Контрольная работа №7. Ряды.

Задания №№ 313, 323, 333, 343, 353.

Задание 313

Исследовать сходимость числового ряда

Решение

Воспользуемся признаком Даламбера

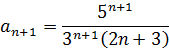
Следовательно, по признаку Даламбера ряд расходится.

Ответ: ряд расходится.

Задание 323

Найти интервал сходимости степенного ряда

Решение

Найдём радиус сходимости степенного ряда

Следовательно, при |x| ˂ 1/e ряд сходится, а при |x| ˃ 1/e ряд расходится.

При |x| = 1/e получаем ряд

По формуле Стирлинга

при , поэтому ряд эквивалентен ряду , который расходится,

Ряд сходится при и расходится при .

При получаем ряд . По формуле Стирлинга и по признаку Лейбница, данный ряд сходится условно, так как он (начиная с некоторого члена) знакопеременный, и модуль общего члена ряда монотонно стремится к нулю.

Ответ:

Задание 333

Вычислить определенный интеграл с точностью до 0,001

Решение

Используем разложение =

Подставим вместо x выражение

Полученный ряд на отрезке [0;1] сходится равномерно, так как на этом отрезке он меньше сходящегося числового ряда

Следовательно, полученное интегрирование законно

Полученный ряд является рядом Лёйбница, поэтому модуль остатка ряда не превосходит модуля первого отбрасываемого члена

Более точно , т.е. точность 0,001 достигнута.

Ответ:

Задание 343

Найти три первых отличных от нуля члена разложения в степенной ряд решения y = y(x) дифференциального уравнения, удовлетворяющего начальному условию

, y(0) = 3

Решение

Подставим начальное условие в дифференциальное уравнение

Продифференцируем уравнения, считая y = y(x)

Три первых ненулевых члена найдено

Ответ:

Задание 353

На интервале задана периодическая с периодом 2π функция f(x). Требуется:

1. Разложить функцию f(x) в ряд Фурье

2. Построить график суммы ряда Фурье

Решение

еcли k = 2n, то

если то

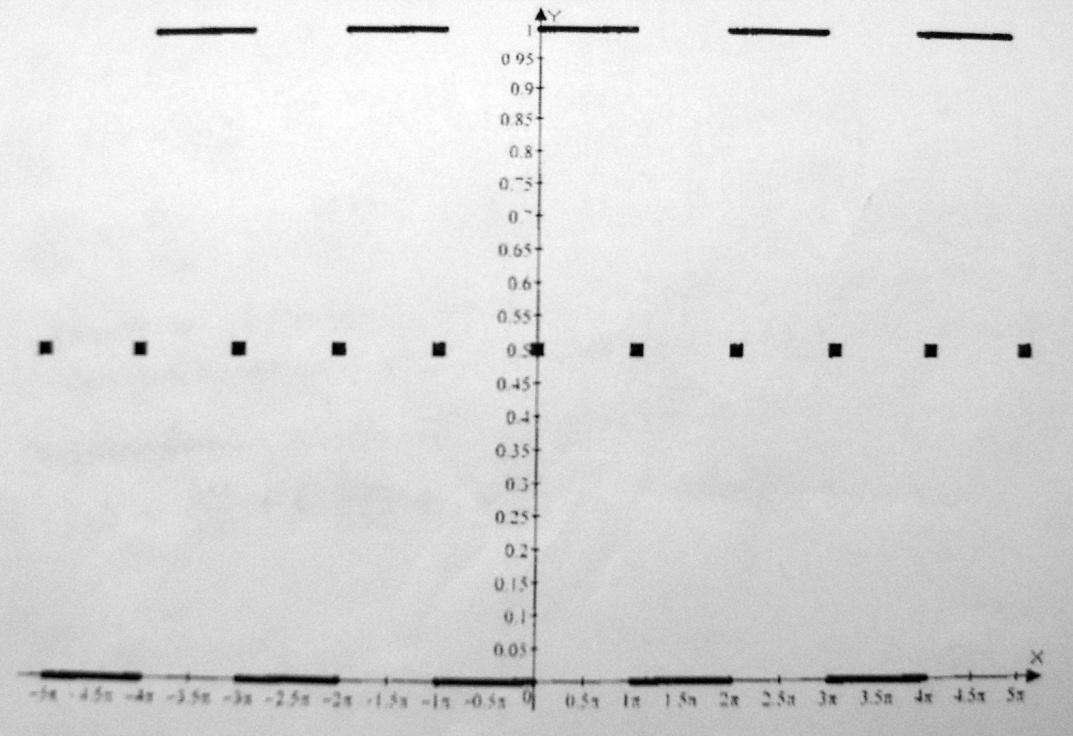
Контрольная работа № 8. Функции комплексной переменной и операционное исчисление.

Задания №№ 363, 373, 383, 393, 403, 413, 423.

Задание 363

Представить заданную функцию w = f(z), где z = x+ iy, в виде w = u(x,y)+i(x,y);

проверить, является ли она аналитической.

Если да, то найти значение её производной в заданной точке

w =

Решение

Пусть z= x+yi, тогда

u (x,y) =

v (x,y) = 3

Проверим выполнение условий Коши-Римана

Условия Коши-Римана выполняются, следовательно, f(z) аналитическая функция.

Подставим x=0 и y=1, получим

Ответ: -2.

Задание 373

Разложить функцию f(z) в ряд Лорана в окрестности точки

,

Решение

Точка существенно особой точкой.

Сначала разложим функцию

Область сходимости

Задание 383

Определить область (круг) сходимости данного ряда и исследовать сходимость его в точках , ,.

Решение

Следовательно, при ряд сходится абсолютно, а при ряд расходится

ряд сходится абсолютно

Если , то получаем ряд - ряд сходится абсолютно, так как ряд из модулей сходится

Задание 393

При помощи вычетов вычислить данный интеграл по контуру l

,

Решение

По теореме о вычетах данный интеграл равен 2πi , умноженному на сумму вычетов во всех особых точках, лежащих внутри контура. Внутри контура лежат полюс первого порядка и полюс второго порядка

Тогда

Задание 403

Найти изображение заданного оригинала

Решение

Применим 2 раза теорему о дифференцировании изображения

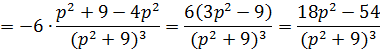
Ответ:

Задание 413

Найти изображение заданного оригинала

Решение

Тогда по теореме об интегрировании изображения

По теореме об интегрировании оригинала

Задание 423

Методом операционного исчисления найти частное решение дифференцированного уравнения, удовлетворяющее заданным начальным условиям

,

Решение

Пусть т.е.

Тогда

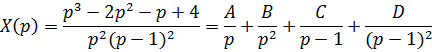
Тогда

Тогда

Ответ: