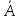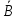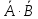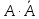ОКП контрольная № 2 вариант 9 (2011г)
.docx«Арифметические основы ЭВМ»
Задание №9
Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы
|
а) 10110112; |
е) 5178; |
л) 1F16; |
|
б) 101101112; |
ж) 10108; |
м) ABC16; |
|
в) 0111000012; |
з) 12348; |
н) 101016; |
|
г) 0,10001102; |
и) 0,348; |
о) 0,А416; |
|
д) 110100,112; |
к) 123,418; |
п) 1DE,C816 |
Решение
а)10110112=1·26+1·24+1·23+1·21=9110
Выполним обратный перевод 9110 в двоичную систему счисления.
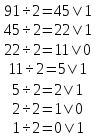
Ответ : 10110112=9110
б) 101101112=1·27+1·25+1·24+1·22+1·21+1·20=18310
Выполним обратный перевод 18310 в двоичную систему счисления.
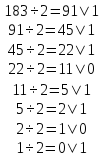
Ответ : 101101112=18310
в) 0111000012=1·27+1·26+1·25+1·20=22510
Выполним обратный перевод 22510 в двоичную систему счисления.
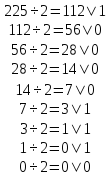
Ответ: 0111000012=22510
г)
|
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
0,54687510 |
1,0937510 |
0,187510 |
0,37510 |
0,7510 |
1,510 |
110 |
0 |
0,10001102=0,54687510
Выполним обратный перевод 0,54687510 в двоичную систему счисления.
0,546875 2
=1, 093750
2
=1, 093750
0,93750
 2
= 0, 187500
2
= 0, 187500
0,187500 2
= 0, 375000
2
= 0, 375000
0,375000 2
= 0, 750000
2
= 0, 750000
0,750000 2
= 1, 500000
2
= 1, 500000
0,500000
 2 = 1, 000000 (дробная часть равна 0 )
2 = 1, 000000 (дробная часть равна 0 )
Ответ: 0,10001102=0,54687510
д) 110100,112=1·25+1·24+1·22+1·2-1+1·2-2=52,7510
Выполним обратный перевод 52,7510 в двоичную систему счисления.
Сначала переведём целую часть 52, а затем дробную 0,75.
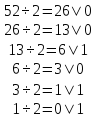
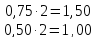 (дробная
часть равна 0)
(дробная
часть равна 0)
Ответ : 110100,112=52,7510
е) 5178=5·82+1·81+7·80=33510
Выполним обратный перевод 33510 в восьмеричную систему счисления
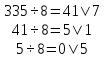
Ответ: 5178=33510
ж) 10108=1·83+1·81=52010
Выполним обратный перевод 52010 в восьмеричную систему счисления
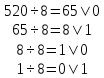
Ответ: 10108=52010
з) 12348=1·83+2·82+3·81+4·80=66810
Выполним обратный перевод 66810 в восьмеричную систему счисления
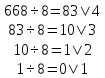
Ответ: 12348=66810
и) 0,348=3·8-1+4·8-2=0,437510
Выполним обратный перевод 0,437510 в восьмеричную систему счисления
0,4375 · 8 = 3,5000
0,5000 · 8 = 4, 0000 (дробная часть равна 0)
Ответ : 0,348=0,437510
к) 123,418=1·82+2·81+3·80+4·8-1+1·8-2=83,51562510
Выполним обратный перевод 83,51562510 в восьмеричную систему счисления
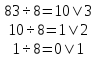
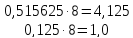 (дробная
часть равна 0)
(дробная
часть равна 0)
Ответ : 123,418=83,51562510
л) 1F16=1·161+F·160=3110
Выполним обратный перевод 3110 в шестнадцатеричную систему счисления
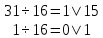
Ответ :1F16=3110
м) ABC16=10·162+11·161+12·160=274810
Выполним обратный перевод 274810 в шестнадцатеричную систему счисления
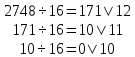
Ответ: ABC16=274810
н) 101016=1·163+1·161=411210
Выполним обратный перевод 411210 в шестнадцатеричную систему счисления
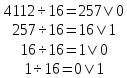
Ответ: 101016=411210
о) 0,A416=10·16-1+4·16-2=0,64062510
Выполним обратный перевод 0,64062510 в шестнадцатеричную систему счисления
0,640625·16=10,25
0,25·16=4,0 (дробная часть равна 0)
Ответ : 0,A416=0,64062510
п) 1DE,C816=1·162+13·161+14·160+12·16-1+8·16-2=478,7812510
Выполним обратный перевод 3110 в шестнадцатеричную систему счисления
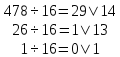
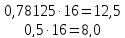 (
дробная часть равна 0 )
(
дробная часть равна 0 )
Ответ : 1DE,C816=478,7812510
Задание №19(Г)
Найдите те подстановки десятичных цифр вместо букв, которые делают правильными выписанные результаты (разные цифры замещаются разными буквами)
ABCD+EFBCA=GHGCIJ
Ответ
A=3, B=6, C=2, D=5, E=9, F=7, G=1, H=0, I=4, J=8;
Задание №22
Разделите 100101102 на 10102 и проверьте результат, умножая делитель на частное.
Решение
100101102÷10102=11112
Проверим умножив частное на делитель
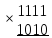
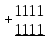
10010110
Ответ : 11112
Задание №25
Расположите следующие числа в порядке возрастания:
а) 1100102, 7010, 3816;
б) 6E16, 11010012, 10010;
Решение
Приведём все числа к одной системе счисление(десятичной)
а) 1100102=5010 3816=6210
Ответ : 1100102 → 3816 → 7010
б) 6E16=11010 11010012=10510
Ответ : 10010 → 11010012 → 6E16
Задание №32
Какой цифрой заканчивается четное двоичное число? Какой цифрой заканчивается нечетное двоичное число? Какими цифрами может заканчиваться четное троичное число?
Ответ : Чётное двоичное число оканчивается - 0 ; нечётное -1 ; чётное троичное - 0 , 1 , 2.
«Логические основы ЭВМ»
Задание № 9
По функциональной схеме записать структурную формулу и построить таблицу истинности.
X Y Z 1 &







Ответ
Формула
- x&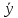 &z
&z
|
x |
y |
z |
|
x& |
|
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
Выражение
истинно лишь при одном условии , когда
значения x
,
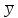 , z
истинны.
, z
истинны.
 Задание
№14
Задание
№14
По структурной формуле построить функциональную схему и составить таблицу истинности.
X
= (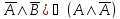
Решение
1 1 &








В А 1 1 & X












|
A |
B |
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |

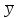
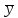 &z
&z