
Контрольная работа по Вышке №1
.doc
![]()
Контрольная работа №1
( по высшей математике для экономических специальностей)
Задачи 1-10. Даны векторы a,b,c,d. Для указанных в пп. 1-3 векторов требуется: 1) вычислить скалярное произведение; 2) найти модуль векторного произведения; 3) проверить коллинеарность и ортогональность;
4) убедиться, что векторы a,b,c образуют базис;
5) найти координаты вектора d в этом базисе.
1. a=i-2j+3k, b=4i+7j+2k, c=6i+4j+2k, d=14i+18j+6k;
1) 3a, 2c; 2) b, -4c; 3) a, c.
Решение:
-
Скалярное произведение вычисляем по формуле (a·b)=a1b1+a2b2+a3b3 (3a·2c)=6(a·c)=6(1·6+(-2)·4+3·2)=6(6-8+6)=24
-
Поскольку скалярное произведение уже известно, из формулы ab=|a|·|b|·cosφ найдем косинус угла между векторами 3a и 2с:
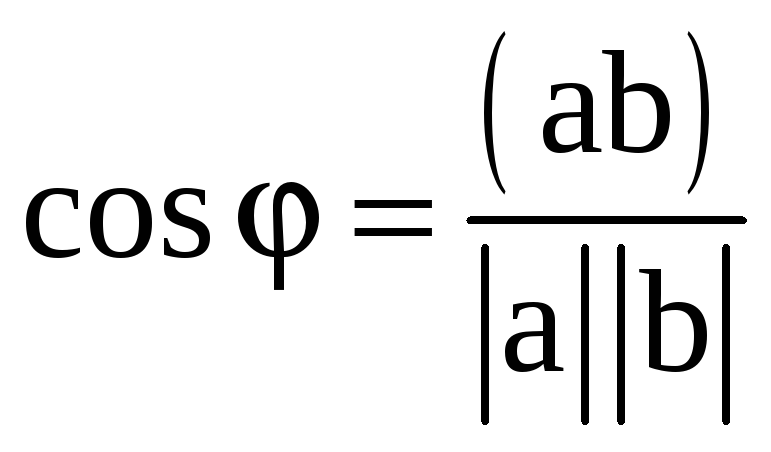 ,
,
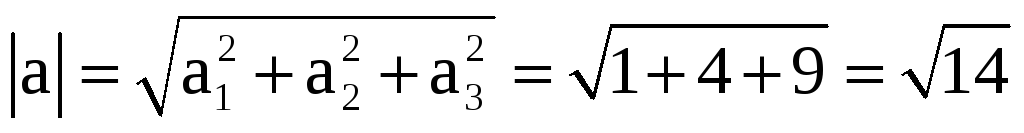

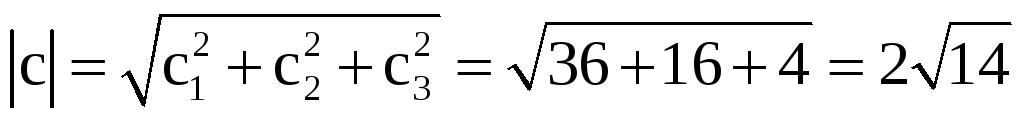
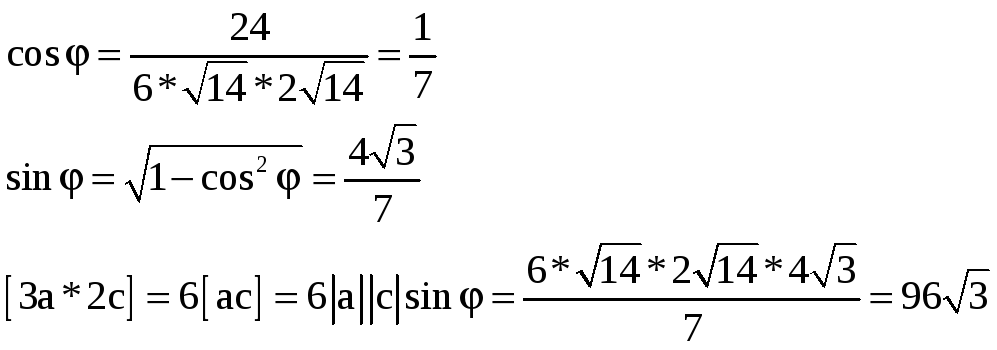
1)3) Поскольку (3a·2c)=24≠0 и |[3a,2с]|=96√3≠0, то согласно условиям ортогональности и коллинеарности двух векторов векторы 3a и 2с – неортогональные и неколлинеарные.
2)1) Скалярное произведение вычисляем по формуле (a·b)= a1b1+a2b2+a3b3
(b·(-4c))=-4(b·c)=-4(4·6+7·4+2·2)=-224
2)2)
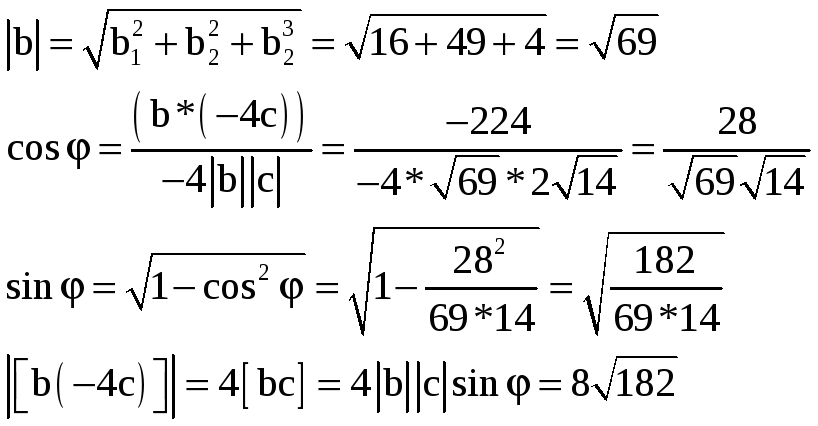
2)3) Поскольку (b·(-4c))=-224≠0 и |[b,-4c]|=8√182≠0, то согласно условиям ортогональности и коллинеарности двух векторов векторы b и -4с – неортогональные и неколлинеарные.
-
(a·c)= (1·6+(-2)·4+3·2)=4
-
Поскольку угол между векторами 3a и 2с равен углу между векторами а и с, то найдем векторное произведение
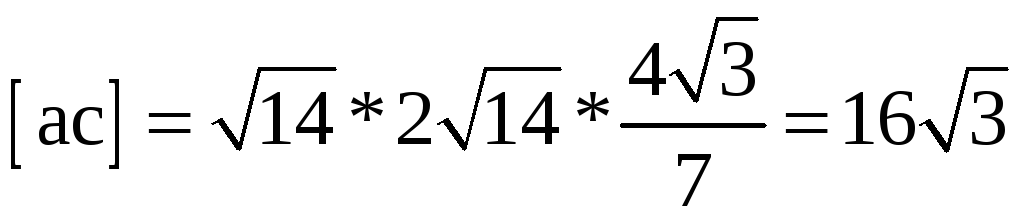
-
Поскольку (a·c)=4≠0 и |[a,c]|=16√3≠0, то согласно условиям ортогональности и коллинеарности двух векторов векторы a и с – неортогональные и неколлинеарные.
-
Найдем смешанное произведение векторов a,b,c по формуле
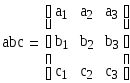
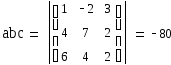
Поскольку abc=-80 ≠0, то векторы линейно независимы и образуют базис.
-
Вектор d можно представить в виде d=xa+yb+zc, что равносильно следующим равенствам: 14=x+4y+6z, 18=-2x+7y+4z, 6=3x+2y+2z.
Решив полученную
систему уравнений, найдем x=0,
y=2, z=1. Итак,
d=2b+c,
вектор d в данном
базисе {a,b,c,}![]() имеет координаты x=0, y=2,
z=1.
имеет координаты x=0, y=2,
z=1.
Задачи 11-20. Даны вершины A(x1, y1), B(x2, y2), C(x3, y3) треугольника ABC.
Требуется найти:
1) уравнение стороны AB;
2) уравнение высоты CH и длину этой высоты;
3) уравнение медианы AM;
4) точку N пересечения медианы AM и CH;
5) уравнение прямой, параллельной стороне AB и проходящей через вершину C;
6) внутренний угол при вершине A и внешний угол при вершине C.
11. A(-2,4), B(3,1), C(10,7).
Решение:
1) Для составления уравнений прямой AB
воспользуемся формулой
![]() .
.
![]() .
Отсюда получим уравнение прямой АВ
3x+5y-14=0.
.
Отсюда получим уравнение прямой АВ
3x+5y-14=0.
2) Прямые CH и AB
перпендикулярны, следовательно,
произведение их угловых коэффициентов
равно -1, т.е.
![]() .
Найдем
.
Найдем
![]() (
(
![]() =
=![]() находим из уравнения прямой AB,
полученного в 1)).
находим из уравнения прямой AB,
полученного в 1)).
Уравнение прямой
с угловым коэффициентом k, проходящей
через точку M(![]() ),
имеет вид
),
имеет вид
![]() .
Уравнение прямой CH,
проходящей через т.С(10,7), имеет вид
.
Уравнение прямой CH,
проходящей через т.С(10,7), имеет вид
y-7=5/3(x-10) или 3y-5x+29=0. Найдем координаты т.Н, решив систему уравнений
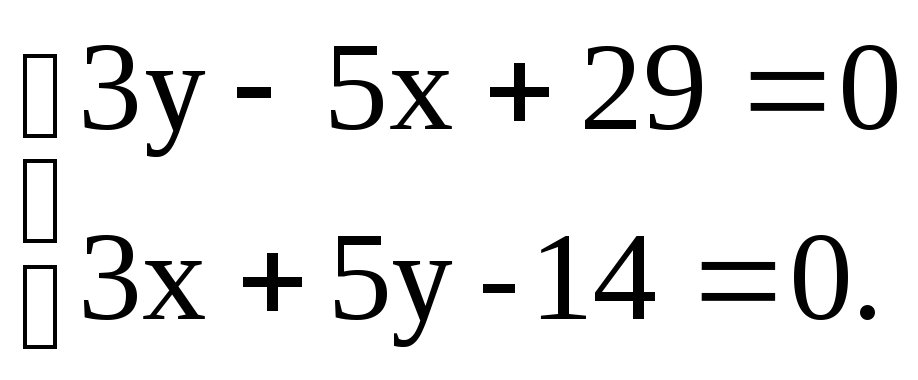 x=5.5, y=-0.5.
Длина высоты CH=
x=5.5, y=-0.5.
Длина высоты CH=
![]() .
.
3) Найдем координаты т.М-середину стороны
ВС.
![]()
![]() .Найдем
уравнение медианы AM.
.Найдем
уравнение медианы AM.
![]() y-4=0.
y-4=0.
4) Для нахождения т.N решим
систему уравнений
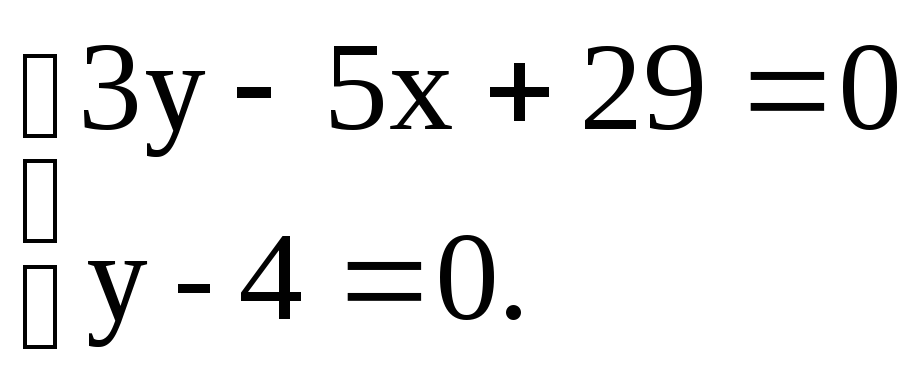 .
Итак, точка N имеет
координаты x=8.2, y=4.
.
Итак, точка N имеет
координаты x=8.2, y=4.
5) Поскольку AB и прямая,
проходящая через т. С, параллельны , то
их угловые коэффициенты равны. Отсюда
уравнений прямой, проходящей через т.
С и параллельной AB, будет
иметь вид
![]() ,
т.е. y-7=
,
т.е. y-7=
![]() или 3x+5y+65=0.
или 3x+5y+65=0.
6) Найдем угловой коэффициент прямой AC
по формуле
![]() .
.
![]() 0,25.
0,25.
Зная
![]() =
=![]() ,
по формуле tgφ=
,
по формуле tgφ=![]() найдем угол BAC.
найдем угол BAC.
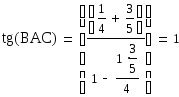 Угол BAC =45˚.
Угол BAC =45˚.
![]()
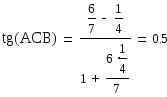 Угол ACВ≈26.6˚. Итак, внешний
угол при вершине С равен 180˚-26.6˚=153.4˚
Угол ACВ≈26.6˚. Итак, внешний
угол при вершине С равен 180˚-26.6˚=153.4˚
Задачи 21-30. Составить канонические уравнения 1) эллипса, 2) гиперболы, 3) параболы по их известным из условий 1-3 параметрам. Через a и b обозначены большая и малая полуоси эллипса или гиперболы, через F - фокус кривой, ε- эксцентриситет, 2c - фокусное расстояние; y= ±kx - уравнения асимптот гиперболы; D - директриса кривой; A, B - точки, лежащие на кривой.
21. 1) b=15, F(-10;0); 2) a=13, =14/13; 3) D: x=-4.
Решение:
1) Каноническое уравнение эллипса
имеет вид x²/a²+y²/b²=1.
Поскольку известны координаты фокуса
F(-10;0), то по формуле с=![]() находим a²=c²+b²=100+225=325.
находим a²=c²+b²=100+225=325.
Отсюда уравнение эллипса с малой полуосью b=15 и фокусом кривой F(-10;0) имеет вид
x ²/ 325+y²/225=1.
2) Каноническое уравнение гиперболы
имеет вид x²/a²-y²/b²=1.
Из ε=c/a
находим c=aε=14
и подставляем в формулу с=![]() .
Откуда b²=c²-a²=196-169=27.
Итак, уравнение гиперболы с эксцентриситетом
=14/13 и большой полуосью a=13 имеет
вид
.
Откуда b²=c²-a²=196-169=27.
Итак, уравнение гиперболы с эксцентриситетом
=14/13 и большой полуосью a=13 имеет
вид
x²/169-y²/27=1.
3) Каноническое уравнение параболы имеет вид y²=2px. Директриса кривой равна x=-4, откуда по формуле x=-p/2 находим p=-2x=8. Отсюда уравнение параболы с директрисой x=-4 имеет вид y²=16x.
Задачи 31-40. Даны четыре точки A1(x1,y1,z1), A2(x2,y2,z2), A3(x3,y3,z4), A4(x4,y4,z4). Требуется найти: 1) уравнение плоскости A1A2A3; 2) уравнение прямой, проходящей через точку A4, перпендикулярно плоскости A1A2A3; 3) расстояние от точки A4 до плоскости A1A2A3; 4) синус угла между прямой A1A4 и плоскостью A1A2A3; 5) косинус угла между координатной плоскостью Oxy и плоскостью A1A2A3.
31. A1(3,-1,2), A2(-1,0,1), A3(1,7,3), A4(8,5,8).
Решение:
1) Для составления уравнения плоскости A1A2A3 воспользуемся формулой
 .
Откуда получаем
.
Откуда получаем
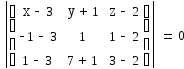 ,
или 9x+6y-30z+39=0
- уравнение плоскости A1A2A3
,
или 9x+6y-30z+39=0
- уравнение плоскости A1A2A3
2) Искомое уравнение прямой, проходящей через т.А4 и перпендикулярной плоскости A1A2A3, получим из канонических уравнений прямой
![]() ,
где
,
где
![]() - точка, лежащая на искомой прямой; m,n,p
- координаты вектора, параллельного
искомой прямой. При этом в качестве
точки
- точка, лежащая на искомой прямой; m,n,p
- координаты вектора, параллельного
искомой прямой. При этом в качестве
точки
![]() возьмем
точку A4(8,5,8) а в качестве вектора
возьмем нормальный вектор плоскости
A1A2A3, т.е. n=(9;6;-30).
Имеем
возьмем
точку A4(8,5,8) а в качестве вектора
возьмем нормальный вектор плоскости
A1A2A3, т.е. n=(9;6;-30).
Имеем
![]() .
.
3) Расстояние от т.
![]() до
плоскости Ax+By+Cz+D=0
вычисляется по формуле
до
плоскости Ax+By+Cz+D=0
вычисляется по формуле
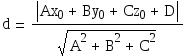 .
Найдем расстояние от точки A4(8,5,8)
до плоскости A1A2A3
.
Найдем расстояние от точки A4(8,5,8)
до плоскости A1A2A3
![]() .
.
4) Синус угла между прямой и плоскостью определяется формулой
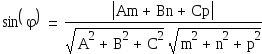 ,
где A, B, C
– координаты нормального вектора
плоскости A1A2A3; m, n, p –
координаты направляющего вектора прямой
A1A4. Найдем координаты вектора
A1A4=(8-3,5+1,8-2)=(5,6,6).
,
где A, B, C
– координаты нормального вектора
плоскости A1A2A3; m, n, p –
координаты направляющего вектора прямой
A1A4. Найдем координаты вектора
A1A4=(8-3,5+1,8-2)=(5,6,6).
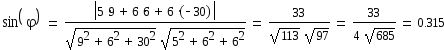 6) Косинус угла
между плоскостями определяется формулой
6) Косинус угла
между плоскостями определяется формулой
![]() .
Поскольку нормальным вектором плоскости
Oxy является координатная
ось Oz, то уравнение
плоскости Oxy примет вид
Сz=0, т.е. косинус угла между
плоскостями Oxy и A1A2A3
будет иметь вид
.
Поскольку нормальным вектором плоскости
Oxy является координатная
ось Oz, то уравнение
плоскости Oxy примет вид
Сz=0, т.е. косинус угла между
плоскостями Oxy и A1A2A3
будет иметь вид
![]() .
.
![]() .
.
