
кр по вышке №3
.docКонтрольная работа № 3
ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Задачи 81-90. 1) Выполнить действия над комплексными числами, записав результат в показательной форме; 2) найти все корни уравнения.
81.1)
![]() ;
2)
;
2)
![]()
Решение:
1) Умножим числитель и знаменатель
выражения
![]() на комплексное число (1+i)7
и получим
на комплексное число (1+i)7
и получим
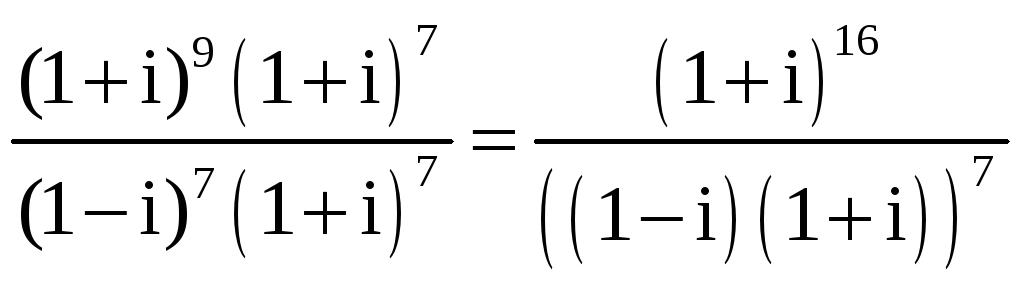 .
Найдем произведение
.
Найдем произведение
![]() ,
а также возведем 1+i в
квадрат
,
а также возведем 1+i в
квадрат
![]() .
Подставив полученные значения в
выражение, найдем
.
Подставив полученные значения в
выражение, найдем
 .
Поскольку i8
представимо в виде i4k,
где k=0,1,2,… , а i4k=1,
то и i8=1. Откуда
.
Поскольку i8
представимо в виде i4k,
где k=0,1,2,… , а i4k=1,
то и i8=1. Откуда
![]() .Представляя
результат в показательной форме, получим
2=reiφ=2e0=2
(где φ=0).
.Представляя
результат в показательной форме, получим
2=reiφ=2e0=2
(где φ=0).
2) Представим комплексное число в
тригонометрической форме:
![]() .
Далее используя формулу
.
Далее используя формулу
![]() ,
получим
,
получим
![]() Подставляя k, φ=0 и
Подставляя k, φ=0 и
![]() ,
найдем
,
найдем
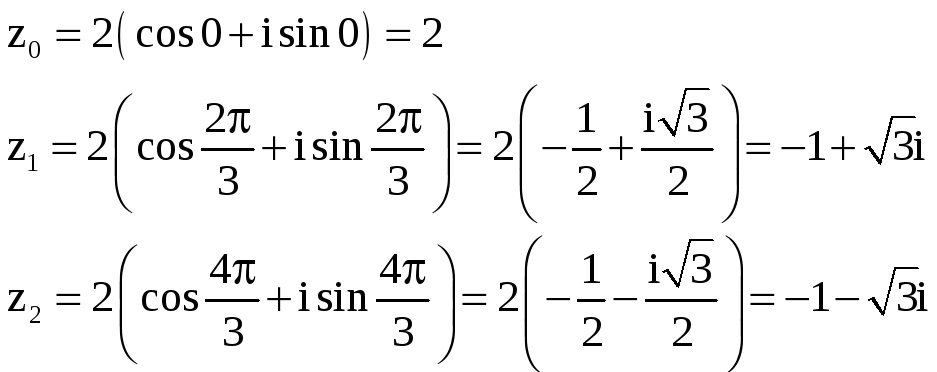
Задачи 91-100. Построить график функции y=F(x), используя преобразования графика известной функции f(x).
91.![]() .
.
Решение:
График функции
![]() на отрезке x=[-10;10] выглядит
следующим образом ( рис.1). Представим
искомый график функции
на отрезке x=[-10;10] выглядит
следующим образом ( рис.1). Представим
искомый график функции
![]() .
График функции
.
График функции
![]() является зеркальным отражением графика
известной функции относительно оси
абсцисс, параллельно смещенной вдоль
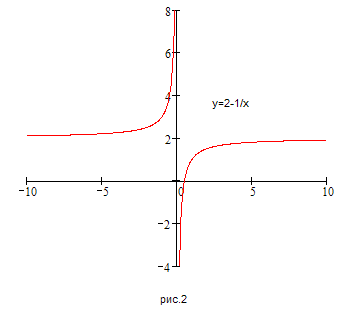
оси ординат на 2 единицы (рис.2). Поскольку
в составе функции выражение в модуле,
то на полуинтервале x=(0;0.5],
участок графика функции, лежащий ниже
оси абсцисс, зеркально отразится
относительно этой оси (рис.3).
является зеркальным отражением графика
известной функции относительно оси
абсцисс, параллельно смещенной вдоль
оси ординат на 2 единицы (рис.2). Поскольку
в составе функции выражение в модуле,
то на полуинтервале x=(0;0.5],
участок графика функции, лежащий ниже
оси абсцисс, зеркально отразится
относительно этой оси (рис.3).


Задачи 101-110. Вычислить пределы функций, не пользуясь правилом Лопиталя.
101. 1)
![]()
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() ;
5)
;
5)
![]() ;
6)
;
6)
![]() .
.
Решение:
1) Непосредственно подставляя аргумент
x=1, получаем в числителе
![]() ,
а в знаменателе бесконечно малую функцию:
,
а в знаменателе бесконечно малую функцию:
![]() .
Поэтому
.
Поэтому
![]()
![]() .
.
2) Подстановка предельного значения
аргумента приводит к неопределенности
![]() .
Разделим числитель и знаменатель на
старшую степень аргумента, т.е. на x3.
Получим
.
Разделим числитель и знаменатель на
старшую степень аргумента, т.е. на x3.
Получим
 ,
так как при
,
так как при
![]() —
бесконечно малые функции.
—
бесконечно малые функции.
3) Подставляя предельное значение
аргумента, получим неопределенность
вида
![]() .
Избавимся от иррациональности в
знаменателе, домножив числитель и
знаменатель на
.
Избавимся от иррациональности в
знаменателе, домножив числитель и
знаменатель на
![]() .
Получим
.
Получим

Подставляя предельное значение аргумента,
получим
 .
.
4) Пределы числителя и знаменателя при
![]() равны 0, т.е. имеем неопределенность
равны 0, т.е. имеем неопределенность
![]() .
Разделим числитель и знаменатель на
3x. Воспользуемся первым
замечательным пределом и получим:
.
Разделим числитель и знаменатель на
3x. Воспользуемся первым
замечательным пределом и получим:
 .
.
5) Разделим числитель и знаменатель на
x и подставим![]() .
.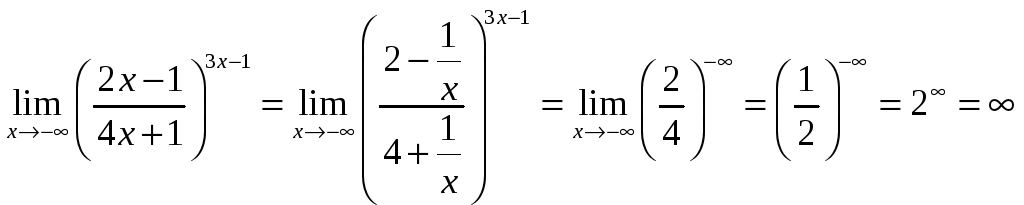 ,
так как при
,
так как при
![]() —
бесконечно малая функция.
—
бесконечно малая функция.
6) Разделим числитель и знаменатель на
x и после преобразований
получим:

В знаменателе получили 12, поскольку
при
![]()
![]() бесконечно малые функции. Произведем
замену
бесконечно малые функции. Произведем
замену
![]()
 .
Используя второй замечательный предел,
найдем
.
Используя второй замечательный предел,
найдем
 .
.
Задачи 111-120. Исследовать функцию f(x) на непрерывность и построить ее график.
111.
|
Решение:
Функция –x непрерывна на
![]() ,
функция (x
1)2 — на
,
функция (x
1)2 — на
![]() ,
функция x 3— на
,
функция x 3— на
![]() ,
значит, f(x) непрерывна на
,
значит, f(x) непрерывна на
![]() .
Остается исследовать точки x1=0
и x2=2. Находим правые
и левые пределы функции в этих точках.
Функция f(x) в точке x1=0
имеет разрыв первого рода, поскольку
правый и левый пределы функции в этой
точке не равны друг другу:
.
Остается исследовать точки x1=0
и x2=2. Находим правые
и левые пределы функции в этих точках.
Функция f(x) в точке x1=0
имеет разрыв первого рода, поскольку
правый и левый пределы функции в этой
точке не равны друг другу:
![]() .
Скачок функции в точке x1=0
равен -1. Функция f(x) в точке x2=2
непрерывна:
.
Скачок функции в точке x1=0
равен -1. Функция f(x) в точке x2=2
непрерывна:
![]() .
.
График функции (рис.1) состоит из 3 частей: 1) y=-x, x 0 ( зеркальное отражение графика функции y=x относительно оси абсцисс); 2) y=-(x-1)2, 0 < x < 2 ( зеркальное отражение графика функции y=x2 относительно оси абсцисс, смещенное вправо вдоль оси абсцисс на 1 единицу); 3) y=x-3, x 2.

