Порядок выполнения работы

При выполнении работы рекомендуется соблюдать следующий порядок исследования: каждый режим выполнять сначала с нейтральным проводом, а потом без него. До включения цепи необходимо на резисторах установить наибольшее сопротивление.

Рассмотрим порядок выполнения опыта при симметричной нагрузке с нейтральным проводом. После включения схемы необходимо изменять сопротивления резисторов таким образом, чтобы фазные токи были равны . При этом вначале на измерительном комплекте ставят фазопереключатель в положение "фаза А" и, регулируя сопротивление проволочного резистора фазы "а", устанавливают в ней ток порядка 1,5 или 2 ампера. Записав в таблицу наблюдений и вычислений показания , , , фазопереключатель ставят в положение "фаза В". Регулируя сопротивление фазы "В", добиваются равенства , после чего заполняют таблицу для фазы "В". Аналогичные действия производят и в фазе "С".

Для обрыва (разгрузки) фаз попользуются выключатели и вмонтированные в фазы приемника.

Несимметричная нагрузка создается изменением сопротивлений приемника , , таким образом, чтобы разность в токах , , была не менее 0,5 А. Причем этот опыт проводится обязательно вначале для звезды с нейтральным проводом. Затем, ничего не изменяя в схеме, размыкают рубильник , создавая схему без нейтрального провода. При этом следует помнить, что если напряжение , будет мало, то надо переключить вольтметр на меньший предел измерения.

Содержание отчета

1. Программа работы.

2. Схема соединений (рис. 3,б).

3. Таблица данных электроизмерительных приборов.

4. Таблица наблюдений и вычислений.

5. Топографические векторные диаграммы по каждому пункту программы.

6. Выводы по работе.

Указания по построению векторных диаграмм

Одним из возможных приемов построения векторных диаграмм по результатам измерений является способ "засечек". Для построения диаграммы линейных напряжений (рис. 4) вектор линейного напряжения в масштабе напряжений (в 1 см - 20 В) необходимо отложить горизонтально, как основание треугольник линейных напряжений.

Из концов его радиусами, равными линейным напряжениям и , циркулем сделаны вверху засечки, точка пересечения которых определяет третью вершину треугольника линейных напряжений . Следует помнить, что этот треугольник во всех режимах остается правильным в силу симметрии линейных напряжений питающей трехфазной сети.

Из вершин этого треугольника радиусами, равными соответствующим фазным напряжениям генератора , сделаны засечки внутри треугольника.

Рис. 4. Векторная диаграмма токов и напряжений

при симметричной нагрузке

Пересечение засечек определит точку « » из которой в вершины треугольника линейных напряжений проводят векторы фазных напряжений генератора , , . Они же будут и векторами фазных напряжений приемника , , , если нейтральная точка приемника « » совпадет с нейтральной точкой генератора « ». Векторы токов , , откладывают в масштабе токов (в 1 см – 0,25 А) по векторам напряжения , , , так как при активной нагрузке ток совпадает по фазе с напряжением.

Векторная диаграмма напряжений и токов, представленная на рис. 4, соответствует случаю симметричной нагрузки приемника, соединенного в звезду с нейтральным и без нейтрального провода. Можно показать, что геометрическая сумма фазных токов равна нулю, т.е. ток в нейтральном проводе отсутствует.

Векторная диаграмма при обрыве одной фазы приемника, соединенного в звезду с нейтральным проводом, показана на рис. 5,а.

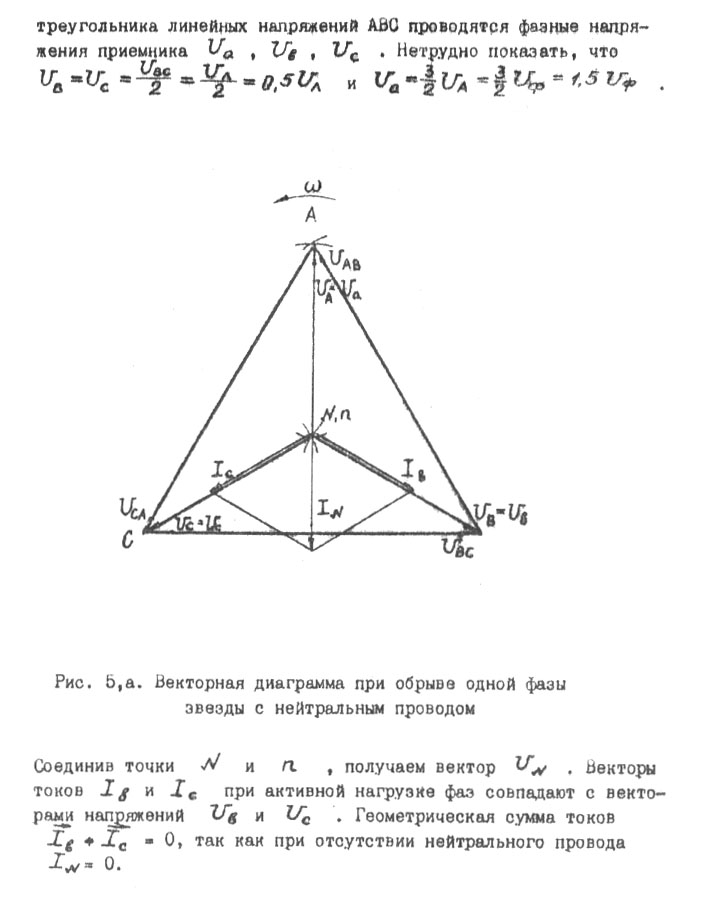
Рис. 5,а. Векторная диаграмма при обрыве одной фазы

звезды с нейтральным проводом

Пусть обрыв имеет фаза "а", тогда . Векторная диаграмма напряжений построена аналогично рис. 4. Токи , совпадают с соответствующими фазными напряжениями , . Ток в нейтральном проводе определяется по уравнению (геометрическая сумма).

Векторная диаграмма при обрыве одной фазы звезды без нейтрального провода показана на рис. 5,б.

Рис. 5,б. Векторная диаграмма при обрыве одной фазы

звезды без нейтрального провода

Построив векторы фазных и линейных напряжений генератора, находим нейтральную точку приемника « ». Для этого радиусами равными фазным напряжениям приемника , , , делаем засечки из вершин треугольника линейных напряжений ABC. Точка пересечения этих засечек и есть точка « ». При обрыве фазы «а» и одинаковых сопротивлениях фаз «в» и «с» точка « » должка оказаться посередине вектора , так как при обрыве фазы "а" получается однофазная цепь с последовательным соединением и (см. рис. 1,а). Эта цепь подключена к линейному напряжению Из-за равенства сопротивлений фаз = напряжение поделится между фазами "в" и "с" пополам. Середина вектора и будет точкой « » (рис. 5,б). Из точки « » в вершины треугольника линейных напряжений АВС проводятся фазные напряжения , , . Нетрудно показать, что

и .

Соединив точки и , получаем вектор . Векторы токов , при активной нагрузке фаз совпадают с векторами напряжений , . Геометрическая сумма токов , так как при отсутствии нейтрального провода .

Векторная диаграмма при обрыве двух фаз (приемника) для звезды с нейтральным проводом показана на риc. 6,а.

При обрыве (разгрузке) двух фаз (а и в) без нейтрального провода трехфазная цепь приемника оказывается разомкнутой и все фазные токи становятся равными нулю: . Напряжение на фазе "с" будет также равно нулю , так как

.

Нейтральная точка « » окажется в вершине "с" треугольника линейных напряжений (рис. 6,б).

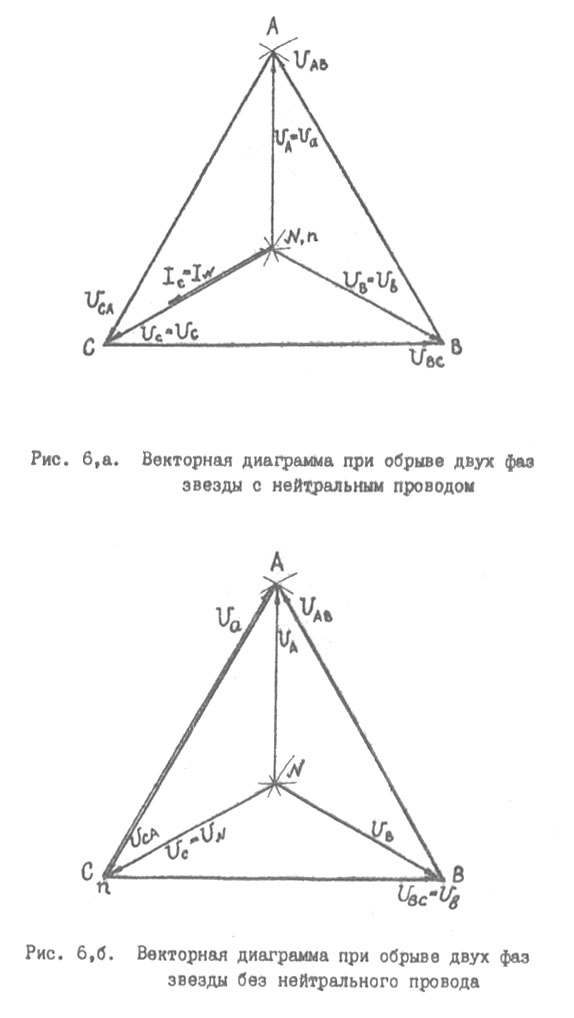
Рис. 6,а Векторная диаграмма при обрыве двух фаз

звезды с нейтральным проводом

Рис. 6,б Векторная диаграмма при обрыве двух фаз

звезды без нейтрального провода

В результате, фазные напряжения разгруженных фаз приемника увеличатся до линейных:

;

.

Напряжение становится равным фазному напряжению генератора .

Векторная диаграмма напряжений и токов для звезды с нейтральным проводом при несимметричной активной нагрузке приведена на рис. 7,а, а для звезды без нейтрального провода на рис 7,б.

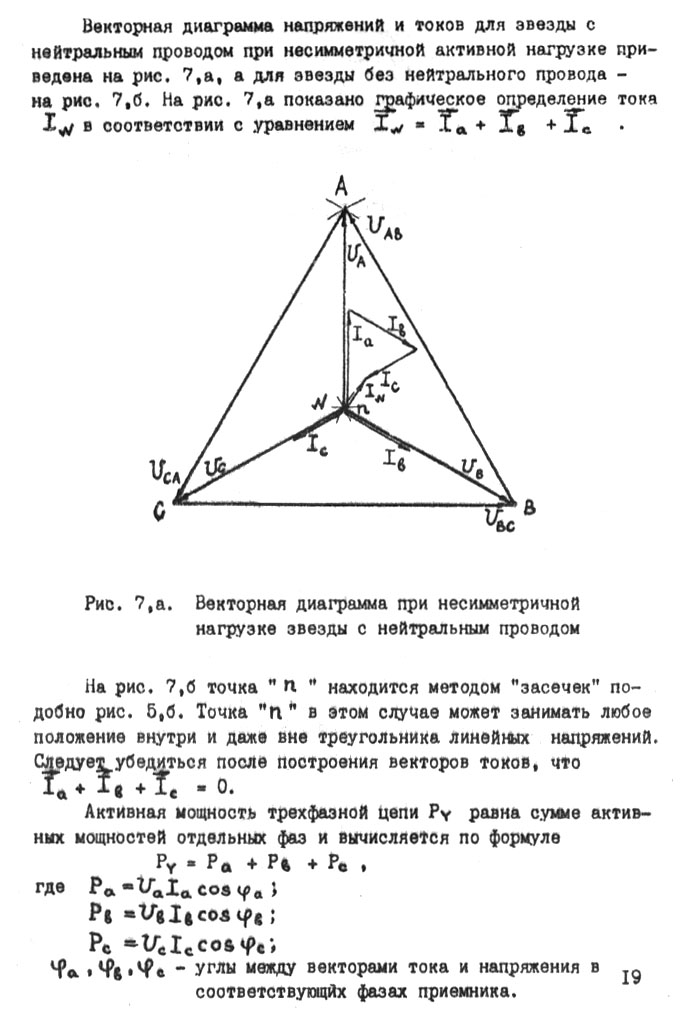
Рис. 7,а Векторная диаграмма при несимметричной

нагрузке звезды с нейтральным проводом

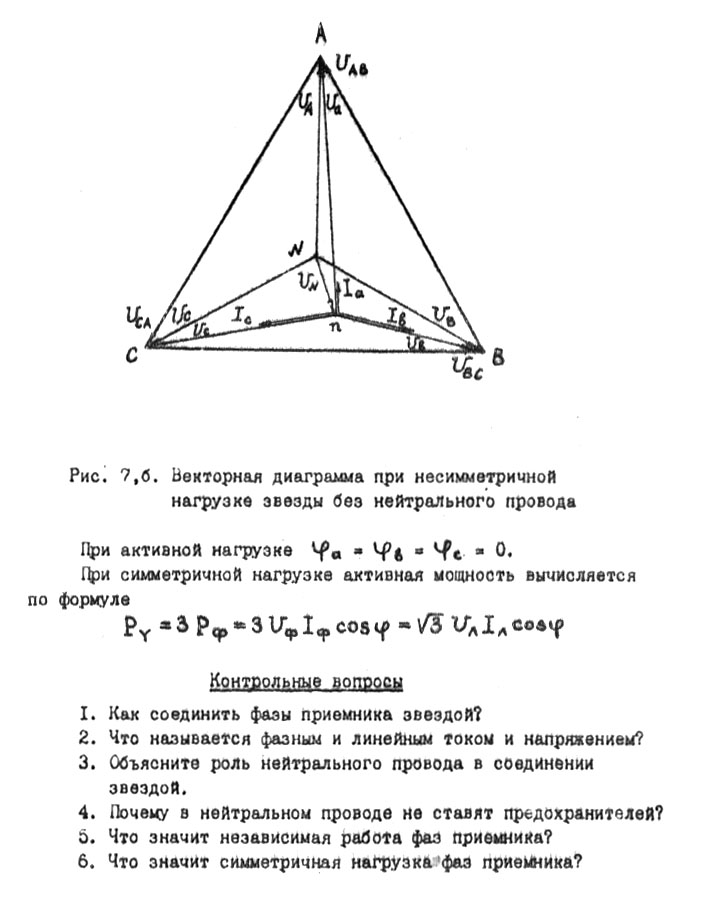
Рис. 7,б Векторная диаграмма при несимметричной

нагрузке звезды без нейтрального провода

На рис. 7,а показано графическое определение тока в соответствии с уравнением .

На рис* 7,б точка « »находится методом "засечек" подобно рис. 5,б. Точка « » в этом случае может занимать любое положение внутри и даже вне треугольника линейных напряжений. Следует убедиться после построения векторов токов, что

.

Активная мощность трехфазной цепи равна сумме активных мощностей отдельных фаз и вычисляется по формуле

,

где

;

;

, , – углы между векторами тока и напряжения в соответствующих фазах приёмника.

При активной нагрузке . При симметричной нагрузке активная мощность вычисляется по формуле

.

Контрольные вопросы

1. Как соединить фазы приемника звездой?

2. Что называется фазным и линейным током и напряжением?

3. Объясните роль нейтрального провода в соединении звездой.

4. Почему в нейтральном проводе не ставят предохранителей?

5. Что значит независимая работа фаз приемника?

6. Что значит симметричная нагрузка фаз приемника?

7