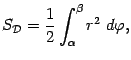Приложения определённого интеграла к геометрическим вычислениям

В главе об определённом интеграле мы уже видели, что для неотрицательной функции величина определённого интеграла

(1)

задаёт площадь криволинейной трапеции , лежащей между отрезком оси и графиком .

Рассмотрим другие геометрические приложения определённого интеграла. Следующее приложение непосредственно следует из формулы (1).

Площадь области, лежащей между двумя графиками

Пусть и  -- две непрерывные функции, заданные на отрезке , причём при всех . Между графиками и лежит область , с боков ограниченная отрезками прямых и .

Рис. 1.

Если обе функции неотрицательны, то есть , то для вычисления площади области достаточно заметить, что она равна разности площадей областей и , лежащих между отрезком (снизу) и, соответственно, графиком и (сверху). Для нахождения площади области и области применим формулу (1) и получим:

(2)

Если же неравенство не выполнено, то заметим следующее: функция ограничена, в том числе снизу, на :

при некотором (по предположению, ). Сдвинем оба графика, и , на единиц вверх, то есть рассмотрим функции и . Тогда, с одной стороны, область между графиками тоже целиком сдвигается на вверх, и её площадь не изменяется; с другой стороны, оба сдвинутых вверх графика окажутся целиком не ниже оси , и площадь между ними можно будет сосчитать по формуле (6.2). Заметим теперь, что

В итоге получаем:

Итак, формула (2) остаётся верной вне зависимости от того, как графики функций и расположены относительно оси .

        Пример 1   Найдём площадь ограниченной области, лежащей между графиками и . Эти графики имеют две общих точки и (см. рис.), причём на отрезке график идёт выше, чем график .

Рис. 2.

Значит, площадь области между графиками равна

    

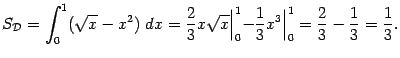
        Пример 2   Найдём площадь ограниченной области , лежащей между графиками и . Решая уравнение , находим, что эти графики пересекаются в трёх точках: , и , причём на отрезке выше расположен график , а на отрезке  -- график . Так как обе функции нечётны, то чертёж обоих графиков симметричен относительно начала координат, и площадь левой части области между графиками (при ) равна площади правой части области (при ).

Рис. 3.

Поэтому искомую площадь можно подсчитать так:

Площадь области, определённой параметрически.

Если область на плоскости снизу ограничена кривой, заданной параметрически, то есть  , при этом  , а сверху – кривой   . Тогда площадь такой плоской фигуры вычисляем по формуле . Эта формула совпадает с формулой вычисления площади в декартовых координатах, если учесть, что  .

Площадь в полярных координатах

Напомним, что определением интеграла служит предел интегральных сумм, взятый при условии измельчения разбиения отрезка интегрирования. Этим определением мы воспользуемся для нахождения площади в следующем случае.

Пусть на плоскости фиксирована система полярных координат: полярными координатами точки служат два числа (  -- полярный радиус,  -- полярный угол).

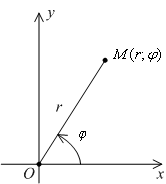
Рис. 4.

Уравнение, задающее зависимость величины от полярного угла ,

задаёт некоторую линию на плоскости. Будем предполагать, что функция непрерывна при . Рассмотрим область на плоскости, расположенную между выходящими из начала координат лучами и и линией (эта область заштрихована на следующем чертеже).

Рис. 5.

Найдём площадь области , вначале приблизив область ступенчатой фигурой следующего устройства. Область изменения угла , то есть отрезок , разобьём на части точками деления

и выберем на каждом участке некоторую отмеченную точку . Получаем размеченное разбиение отрезка . Приближённо будем считать площадь сектора области , лежащего между лучами и , равной площади кругового сектора с тем же центральным углом и радиусом, равным (см. рис.):

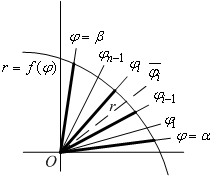
Рис. 6.

Площадь кругового сектора подсчитывается по формуле

Значит, площадь всей области приближённо равна интегральной сумме

построенной по выбранному размеченному разбиению отрезка для функции

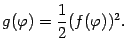
При неограниченном измельчении разбиения , то есть при условии , эта интегральная сумма будет стремиться к площади области . С другой стороны, предел интегральных сумм для функции даст определённый интеграл от этой функции. Таким образом, получаем формулу площади:

Более кратко эту формулу можно записать так:

(3)

где имеется в виду, что вместо полярного радиуса нужно подставить его выражение через полярный угол для зависимости, график которой ограничивает область снаружи.

        Пример 3   Найдём площадь области, ограниченной частью спирали ( ) при и отрезком оси (см. рис.).

Рис 7.

Применяя формулу (3), получаем:

    

Если область имеет границу, состоящую из двух отрезков лучей и (эти отрезки могут вырождаться в одну точку) и двумя линиями, заданными уравнениями в полярных координатах: и , причём при всех (см. рис.), то площадь области можно представить как разность двух площадей:  -- площади области, лежащей между лучами , и линией , -- и  -- площади области, лежащей между лучами , и линией .

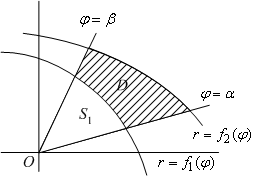
Рис. 8.

Каждую из площадей и можно подсчитать по формуле (3), так что получаем в итоге

(4)