Вычислительные методы и методы оптимизации в экономике

Вариант 6

Задание 1

Задача 1. Решить СЛАУ методом Гаусса

Решение.

Решение в Excel

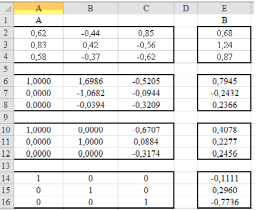
Решение в MathCad

Задача 2. Решить СЛАУ методом квадратного корня

Решение.

Матрица А не является положительно определенной (есть отрицательное собственное значение), поэтому невозможно найти решение матрицы методом квадратного корня.

Решение в MathCad

Задание 2

1. Построить итерационный многочлен Лагранжа для функции с заданными узлами

2. вычислите его значение точке .

3. определить относительную погрешность.

, х₀= –4, х₁= –3, х₂= -1, х₃= 0, = –2,057.

Решение.

,

Относительная погрешность

Решение в MathCad

х₀ := –4 х₁ := –3 х₂ := -1 х₃= 0

Задание 3. Методом наименьших квадратов найти эмпирическую функцию вида для данных, представленных таблицей, и построить график найденной функции и исходных точек в одной системе координат

Х	1	2	3	4	5
Y	1,9	1,4	3,4	4,9	3,9

Решение.

ИТОГО

Х	1	2	3	4	5	15
Y	1,9	1,4	3,4	4,9	3,9	20
X^2	1	4	9	16	25	55
X*Y	2,8	4,6	12,9	23,2	24	67,5

Рассчитаем параметры уравнения

Подставляя значения из таблицы 2, получим

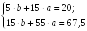
Решим систему, получим

Построенное уравнение парной регрессии:

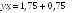
Решение в MathCad

Задание 4. Вычислить определенный интеграл с помощью формулы Симпсона и средних прямоугольников

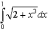
Решение.

Формула средних прямоугольников

Формула Симпсона

Решение в MathCad

Метод средних прямоугольников

Задание 5. Отделить корни уравнения аналитически и уточнить корень методом Ньютона

Решение.

Построим кривые

,

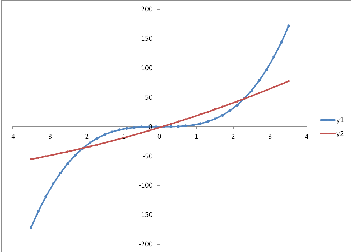
Уравнение имеет три корня:

, ,

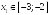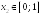Уточним корень . Используем метод Ньютона.

x	f(x)	f '(x)
2	-1	33
2,0303	0,0231	34,5262
2,0296	0,0000	34,4923
2,0296	0,0000	34,4923

Корень равен:

Решение в MathCad

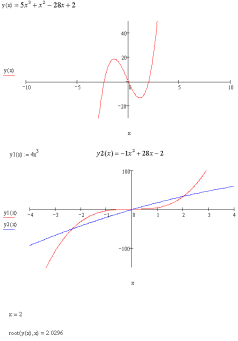
Задание 6. Составить таблицы приближенных значений решения дифференциального уравнения , удовлетворяющего начальному условию , на отрезке [1; 2] с шагом h = 0,2. С помощью методов Эйлера и Рунге -Кутта. Определить относительную погрешность.

Решение.

Найдем решение дифференциального уравнения

Подстановка: ,

, , , ,

, , ,

, , ,

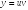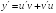
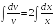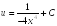
, – общее решение.

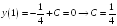
– частное решение

_{Метод Эйлера}

, .

Произведем расчеты

№	x	y	f(x,y)	h	Y	Delta %
0	1	0	1	0,2	0,0000	0
1	1,2	0,2000	0,9120		0,1864	7,30
2	1,4	0,3824	0,9107		0,3624	5,51
3	1,6	0,5646	0,9498		0,5423	4,10
4	1,8	0,7545	1,0098		0,7328	2,96
5	2	0,9565			0,9375	2,02

Y – точное решение.

_{Метод Рунге-Кутта}

.

№	x	y	h	k1	k2	k3	k4	Y	Delta %
0	1	0,0000	0,2	0,2	0,1866	0,1842	0,1771	0,0000	0
1	1,2	0,1865		0,1779	0,1758	0,1754	0,1763	0,1864	0,04
2	1,4	0,3626		0,1765	0,1795	0,1799	0,1844	0,3624	0,03
3	1,6	0,5425		0,1845	0,1901	0,1907	0,1972	0,5423	0,03
4	1,8	0,7330		0,1972	0,2042	0,2050	0,2126	0,7328	0,03
5	2	0,9378						0,9375	0,03

Решение в MathCad

_{Метод Эйлера}

_{Метод Рунге-Кутта}

Задание 7. Решить систему нелинейных уравнений методом простои итерации, проверив условие сходимости.

Решение.

Проверим условие сходимости

, , ,

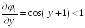Условие сходимости выполняется.

Система имеет корень при: и

№	x	y	Dx	Dy	D
0	1	0
1	1,6415	1,3000	0,6415	1,3000	1,3000
2	1,5457	0,7016	0,0958	0,5984	0,5984
3	1,7915	0,7810	0,2457	0,0794	0,2457
4	1,7780	0,5886	0,0135	0,1924	0,1924
5	1,7998	0,5981	0,0218	0,0095	0,0218
6	1,7996	0,5828	0,0002	0,0154	0,0154
7	1,7999	0,5829	0,0003	0,0001	0,0003
8	1,7999	0,5827	0,0000	0,0002	0,0002
9	1,7999	0,5827	0,0000	0,0000	0,0000

Решение системы: (1,7999; 0,5827)

Задание 8.

Задача 1. Решить задачу линейного программирования графическим методом

Решение.

Построим многоугольник решений.

Построим граничные прямые:

Определим полуплоскости, в которых выполняются неравенства системы ограничений, найдем область решения неравенств – не ограниченная область.

Вектор градиентного направления 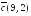указывает направление наискорейшего возрастания функции. Строим вектор .

Перпендикулярно вектору проводим линию уровня . В данном случае строим прямую . Перемещаем прямую в градиентом направлении до крайней точки в области .

Минимальное значение функция принимает в точке А.

Максимальное значение функция принимает в точке С.

Решение в MathCad

Задача 2. В животноводческом совхозе на производство 1 ц молока тратится 25 ден. ед., из них на трудовые затраты – 10 ден.ед., на материальные затраты – 15 ден. ед.; производство 1 ц мяса обходится в 180 ден. ед., из которых 100 ден. ед. – трудовые затраты, 80 ден. ед. – материальные. Государственные закупочные цены: за 1 ц молока – 35 тыс. ден. ед., а за 1 ц мяса – 200 тыс. ден. ед. Определить прибыль от реализации. Фонд зарплаты – 100 тыс. ден. ед., остальные на оборудование.

Решение.

Построим экономико-математическую модель задачи.

Обозначим через (= 1, 2) количество продукции П1 иП2, соответственно.

Подставляя данные из условия задачи получим:

Ограничения будут выражены следующими равенствами:

Решение задачи в пакете Excel:

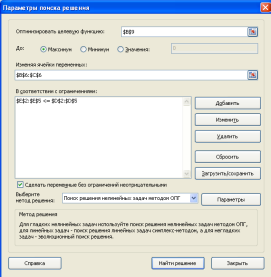
Решение в MathCad

Задание 9. Найти минимальное значение функции и точку , в котором оно достигается, методом золотого сечения.

Решение.

Определим отрезок, содержащий минимальное значение функции

Решение в MathCad

23