
контрольная работа по ПМ
.docxУчреждение образования «Белорусский государственный университет информатики и радиоэлектроники»
Кафедра программного обеспечения информационных технологий
Контрольная работа № 1
(вариант 10)
по дисциплине
Прикладная математика
Минск 2010
Задача № 1. Для графов G1 и G2 (рис. 10.1) построить графы G1G2, G1G2, G1(G2), G2(G1), матрицы смежности вершин А(G1), А(G2) и матрицы инцидентности В(G1), В(G2), введя предварительно нумерацию дуг. По матрицам смежности вершин исходных графов построить матрицы смежности вершин А(G1G2), А(G1G2), А(G1(G2)), А(G2(G1)). Будут ли изоморфны графы G1(G2) и G2(G1)?

Рис. 10.1
Решение:
G1G2
G1G2

G1(G2)
|
G1 |
G2 |
G1(G2)
|
|
1,2 |
2,2 2,1 |
1,2 1,1 |
|
1,3 |
3,3 3,1 |
1,3 1,1 |
|
1,4 |
4,4 |
1,4 |
|
2,2 |
2,2 2,1 |
2,2 2,1 |
|
3,2 |
2,2 2,1 |
3,2 3,1 |
|
3,3 |
3,3 3,1 |
3,3 3,1 |
|
3,4 |
4,4 |
3,4 |
|
3,1 |
1,4 |
3,4 |
Исключив
кратные дуги построим граф G1(G2)


2
3









1
4




G2(G1)
|
G2 |
G1 |
G2(G1)
|
|
1,4 |
|
|
|
2,1 |
1,2 1,3 1,4 |
2,2 2,3 2,4 |
|
2,2 |
2,2 |
2,2 |
|
3,1 |
1,2 1,3 1,4 |
3,2 3,3 3,4 |
|
3,3 |
3,1 3,2 3,4 |
3,1 3,2 3,4 |
|
4,4 |
|
|
Исключив
кратные дуги построим граф G1(G2)


2







3
4
1


Матрицы смежности вершин:


Матрицы инцидентности:


По матрицам смежности вершин исходных графов построим матрицы смежности вершин:


Так как, матрицы смежности вершин графов G1(G2) и G2(G1) не получаются друг из друга одинаковыми перестановками строк и столбцов данные графы не изоморфны.


Задача № 2.
При условии, что петля считается двойным
ребром, для графов G1
и G2
(рис. 10.2)
построить матрицы смежности вершин
А(G1)
и А(G2),
введя предварительно нумерацию рёбер,
построить матрицы инцидентности В(G1)
и В(G2).
По матрицам смежности вершин исходных
графов построить матрицы смежности
вершин А(G1G2)
и А(G1G2).
Рис. 10.2
Матрицы смежности вершин:


Матрицы инцидентности:


Матрицы смежности вершин А(G1G2) и А(G1G2):
А(G1G2)

А(G1G2)

Задача № 3.
Построить код (G)
по дереву G
(рис. 10.3)
и восстановить G.
.
3 9
2 7
1 5 8
4 6 Рис. 10.3

(2)

(2, 1)

(2,1,1)

(2,1,1,5)

(2,1,1,5,5)

(2,1,1,5,5,5)
8

(2,1,1,5,5,5,7)
Построение дерева:
2
3
(2,1,1,5,5,5,7)

(1,1,5,5,5,7)

(1,5,5,5,7)

(5,5,5,7)

(5,5,7)

(5,7)

(7)

Задача № 4. По алгоритму Краскала построить для нагруженного графа G, изображенного на рис. 10.4, минимальный каркас G1 с указанием последовательности выбора рёбер ei.Определить вес построенного каркаса (G1).
v2
4 v6
3 2
1 3 3 1 v9 1 v7
v1 2 v3 2 v5 2 1
1 1 1 v8
3 3 3 2
v4 5 v10


µ(G)=1+1+1+1+2+2+1+1+2=12
число шагов равно p-1=9
Задача № 5. В графе G, изображённом на рис. 10.5, найти все минимальные внешне устойчивые множества вершин, наименьшие доминирующие множества и число внешней устойчивости (G).

Решение:

Составим логическую функцию согласно



Данная ДНФ является сокращённой и минимальной, т.к. переменные входящие в состав всех импликант, независимы.
Выбираем вершины, для которых оценки переменных вошли в состав элементарных конъюнкций:

Число внешней устойчивости (G)=2.
Задача № 6.
Построить максимальный поток и разрез
с минимальной пропускной способностью
в транспортной сети, приведённой на
рис. 10.6, по алгоритму Форда-Фалкерсона.
Решение:
В
сети пропущен поток
 .
.
Шаг
1. Помечаем
узел s
пометкой
 .
.
Шаг
2. Из
узла s
можно пометить узел b
 ,
из узла b
можно пометить узел d
,
из узла b
можно пометить узел d
 ,
из узла d
можно пометить узел t
,
из узла d
можно пометить узел t
 .
.
Шаг
3. Построен
(s,
t)
– путь, насыщающий поток, {s,b,d,t},
состоящий из трех прямых дуг
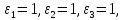 следовательно
следовательно
 .
На дугах (s,b),
(b,d),
(d,t)
увеличиваем значение потока на 1, тем
самым построен новый поток
.
На дугах (s,b),
(b,d),
(d,t)
увеличиваем значение потока на 1, тем
самым построен новый поток
 .
.
Шаг 1. Помечаем
узел s
пометкой
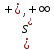 .
.
Шаг 2. Из
узла s
можно пометить только узел a
 ,
из узла a
можно пометить узел b
,
из узла a
можно пометить узел b
 и узел d
и узел d
 ,
из узла b
никакой узел пометить нельзя т.к. дуга
(e,b)
обратная к b
и имеет f(e)=0,
а дуги (s,b)
и (b,d)
имеют f(e)=c(e),
из узла d
так же нельзя пометить никакой узел
т.к. дуги (d,t)
и (d
,b)
имеют f(e)=c(e).
,
из узла b
никакой узел пометить нельзя т.к. дуга
(e,b)
обратная к b
и имеет f(e)=0,
а дуги (s,b)
и (b,d)
имеют f(e)=c(e),
из узла d
так же нельзя пометить никакой узел
т.к. дуги (d,t)
и (d
,b)
имеют f(e)=c(e).
Для выделения подчеркнем все помеченные и просмотренные узлы.
s
 .
.
a
 ,
,
b

c
d
 ,
,
e
t
Таким
образом в сети построен разрез
( )={(s,c),(b,e),(d,t)},
где X={s,a,b,d,},
)={(s,c),(b,e),(d,t)},
где X={s,a,b,d,},
 ={c,e,t},
с пропускной способностью c(
={c,e,t},
с пропускной способностью c( )=3+5=8
и максимальный поток
)=3+5=8
и максимальный поток
 =8.
=8.
Задача № 7. Доказать справедливость тождества для произвольных множеств А, B и C:
А\(ВC)=(А\B)(A\C).
Решение:
Рассмотрим левую сторону тождества:

используя
закон де Моргана получим: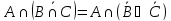 .
.
Рассмотрим правую сторону тождества:
(А\B)(A\C)=
(А )(A
)(A );
);
используя дистрибутивный закон алгебры множеств получим:
(А )(A
)(A )=
)= .
.
Таким образом тождество доказано.
Задача № 8. Доказать, что множества Х и Y равномощны, построив взаимно-однозначное соответствие между ними.
Х=[0,1][3,5], Y=[0,1).
Решение:
Используя
свойства несчётных множеств построим
взаимно-однозначное соответствие
множеств Х и Y:


Задача № 9. Даны три вещественных функции:
f(x)=2x11–3,
 ,
h(x)=
–9sin(12x)+3.
,
h(x)=
–9sin(12x)+3.
1) Найти заданные композиции функций: fgh, hfg, fhf.
2) Являются ли f, g, h инъекциями, сюръекциями, биекциями на R?
3) Найти обратные функции к f, g, h. Если функции со своими областями определения обратных не имеют, то найти обратные функции к их сужениям.
Решение:
1) D(f)=D(g)=D(h)=R, поэтому все три указанные композиции функций определены на R.




2) Рассмотрим
функцию f(x)=2x11–3.
Производная функции
 =22x10>0
для всех xR\{0},
поэтому f
является строго возрастающей функцией
на (–,0)(0,+).
=22x10>0
для всех xR\{0},
поэтому f
является строго возрастающей функцией
на (–,0)(0,+).
 =0,
f(0)= –3f()
для 0.
Поэтому f
инъективна.
=0,
f(0)= –3f()
для 0.
Поэтому f
инъективна.
Функция
f
непрерывна на R.
 и
и
 .
Поэтому f
является сюръекцией на R.
Итак, f:
RR
– биекция.
.
Поэтому f
является сюръекцией на R.
Итак, f:
RR
– биекция.
Рассмотрим
функцию
 .
Производная функции g
для
.
Производная функции g
для
 не является строго возрастающей на всей
области определения R.
Поэтому g
– не инъекция. Поскольку–1/4<g(x)<1/4
для всех хR.
Значит, g
не является сюръекцией на R.
Итак,
g:
RR
не является биекцией.
не является строго возрастающей на всей
области определения R.
Поэтому g
– не инъекция. Поскольку–1/4<g(x)<1/4
для всех хR.
Значит, g
не является сюръекцией на R.
Итак,
g:
RR
не является биекцией.
Рассмотрим
функцию h(x)=
–9sin(12x)+3.
Производная функции h
для
 не является строго возрастающей на всей
области определения R.
Поэтому h
– не инъекция. Поскольку–1≤
sin(12x)≤1
для всех хR,
то
–6≤g(x)
≤12
для всех хR.
Значит, h
не является сюръекцией на R.
Итак,
h:
RR
не является биекцией.
не является строго возрастающей на всей
области определения R.
Поэтому h
– не инъекция. Поскольку–1≤
sin(12x)≤1
для всех хR,
то
–6≤g(x)
≤12
для всех хR.
Значит, h
не является сюръекцией на R.
Итак,
h:
RR
не является биекцией.
3) Поскольку f: RR – биекция, то по теореме 3.1 на R существует обратная функция к f – f –1: RR.
2x11–3=y;


Итак,
 ,
xR.
,
xR.
Для g: E(g)=(–1/4, 1/4).
 ;
;



Итак,

 x(–1/4,
1/4).
x(–1/4,
1/4).
Для h: E(h)=(–6, 12).
-9sin(12x)+3=y;
-9sin(12x)=y-3;
 ;
;
 ;
;
Итак,
 ,
x(–6,
12).
,
x(–6,
12).
Задача № 10. Является ли антирефлексивным бинарное отношение R–1, если отношение R антирефлексивно? В случае отрицательного ответа необходимо привести конкретный пример.
Решение:
Пусть RХ2 для некоторого множества Х. Т.к. R антирефлексивно, то для любого хХ хRх - ложно. Поэтому, по определению R–1, для любого хХ хR–1x-ложно. Т.е. R–1 антирефлексивно на Х.
