
- •Министерство образования и науки украины
- •Рассмотрено на заседании кафедры
- •Тема курсовой работы: «Построение аналитических моделей алгоритмов и оценка их сложности
- •4. Реализовать функцию над числами в унарном коде.
- •5. Реализовать функцию над числами в унарном коде.
- •6. Реализовать функцию над числами в унарном коде.
- •Приложение а Техническое задание Приложение б Руководство пользователя.
Министерство образования и науки украины
ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ВЫПОЛНЕНИЯ КУРСОВОЙ РАБОТЫ ПО КУРСУ
ТЕОРИЯ АЛГОРИТМОВ И ВЫЧИСЛИТЕЛЬНЫХ ПРОЦЕССОВ
(для студентов специальности 7.080403 «Программное обеспечение вычислительной техники и автоматизированных систем», «Компьютерный эколого-экономический мониторинг»)
Рассмотрено на заседании кафедры
Прикладной математики и информатики
Протокол № __9__ от «4»_02______2009г.
Донецк 2009
Методические указания к выполнению курсовой работы по курсу «Теория алгоритмов и вычислительных процессов» (для студентов специальностей «Программное обеспечение вычислительной техники и автоматизированных систем», «Компьютерный эколого-экономический мониторинг»)
Сост.: Коломойцева И. А., Назарова И.А.
Тема курсовой работы: «Построение аналитических моделей алгоритмов и оценка их сложности
Задание на курсовую работу:
1. Рекурсивные функции
Разработать алгоритм вычисления
![]() в виде рекурсивной функции. Проверить
модель алгоритма на множестве тестовых
примеров. Определить к какому классу
рекурсивных функций принадлежит
:
примитивно-рекурсивна, частично
рекурсивна или общерекурсивна.
в виде рекурсивной функции. Проверить
модель алгоритма на множестве тестовых
примеров. Определить к какому классу
рекурсивных функций принадлежит
:
примитивно-рекурсивна, частично
рекурсивна или общерекурсивна.
2. Машины Тьюринга
2. 1.Описать системой команд, функциональной таблицей и диаграммой переходов работу машины Тьюринга, реализующую заданный вариантом алгоритм. Начальная и конечная конфигурации стандартны. Проверить модель алгоритма на множестве тестовых примеров. Привести последовательности конфигураций машины Тьюринга для различных тестовых исходных слов.
2.2. Построить машину Тьюринга, вычисляющую
функцию
![]() из задания №1 “Рекурсивные функции”.
Машину Тьюринга представить как
композицию элементарных МТ, выполняющих
операции: копирование аргумента,
сложение, умножение, арифметическое
вычитание, нахождение целой части и
остатка от деления, сравнения чисел,
выделение аргумента. Недостающие
элементарные МТ описать любым известным
способом.
из задания №1 “Рекурсивные функции”.
Машину Тьюринга представить как
композицию элементарных МТ, выполняющих
операции: копирование аргумента,
сложение, умножение, арифметическое
вычитание, нахождение целой части и
остатка от деления, сравнения чисел,
выделение аргумента. Недостающие
элементарные МТ описать любым известным
способом.
2.3. Определить машину Тьюринга, распознающую заданный язык. Программно реализовать эту машину и построить график ее временной сложности T(n) (для n, требующих 3-5 мин. счета).
3. Нормальные алгоритмы Маркова
Составить нормальный алгоритм Маркова над алфавитом А. На конкретных примерах исходных слов продемонстрировать работу составленных алгоритмов.
Варианты заданий к заданию №1
Сумма всех делителей числа
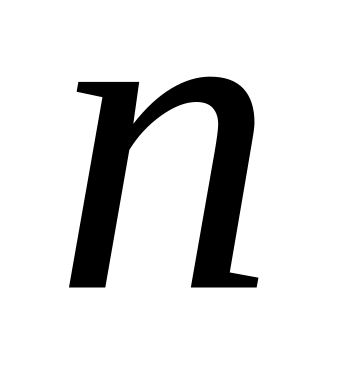 .
.Количество делителей числа .
Количество нулей в двоичной записи .
Сумма цифр в двоичной записи .
Количество взаимно-простых с чисел,
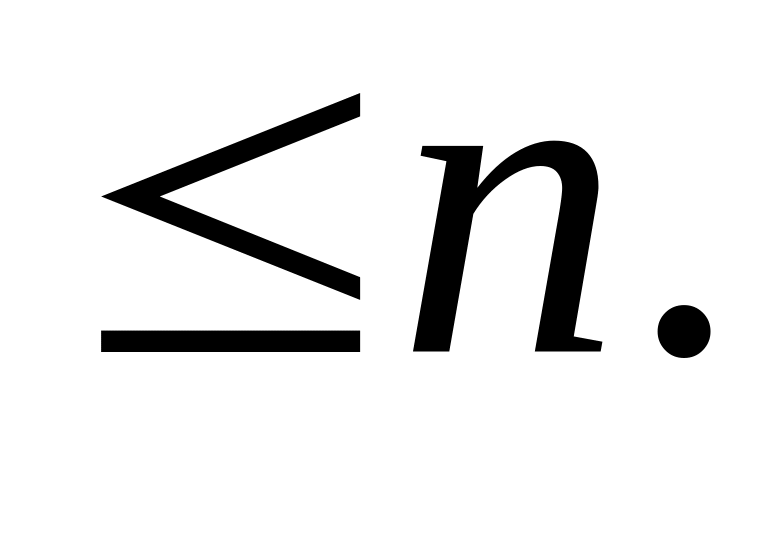
Максимум из двух чисел
 и
и
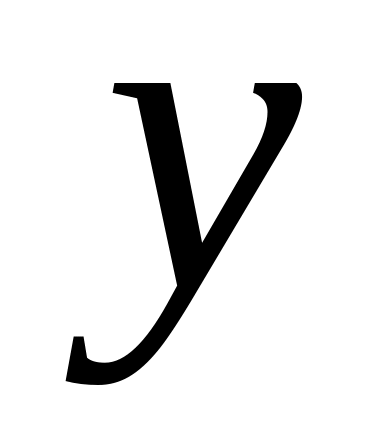 ,
,
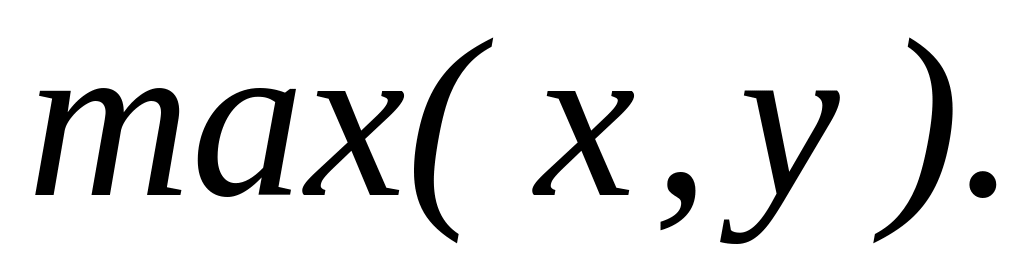
Минимум из двух чисел и ,
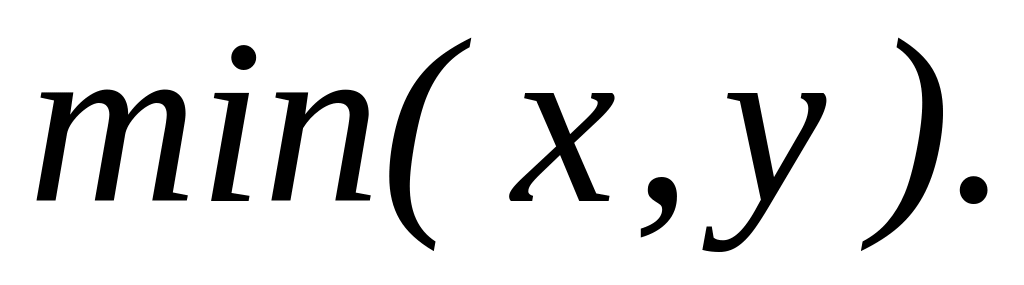
Модуль разности двух чисел и ,
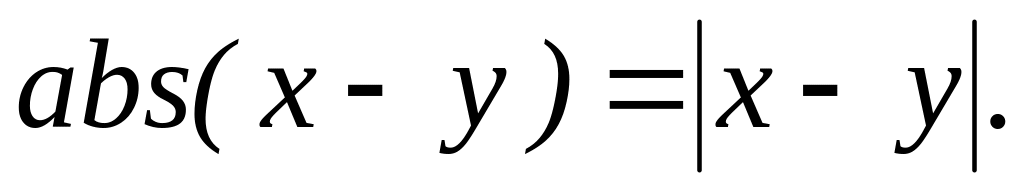
Максимальная цифра в 8-ричной записи числа .
Минимальная цифра в 8-ричной записи числа .
Количество четных цифр в 8-ричной записи числа .
Количество нечетных цифр в 8-ричной записи числа .
Сумма простых делителей числа .
Количество простых делителей числа .
Количество простых чисел,
Количество чисел, являющихся полными квадратами,
Сумма чисел, являющихся степенью двойки,
Максимальная цифра в 16-ричной записи числа .
Минимальная цифра в 16-ричной записи числа .
Ближайшее к простое число.
Произведение делителей числа .
Произведение простых делителей числа .
Произведение взаимно-простых с чисел,
Наименьшее общее кратное двух чисел,
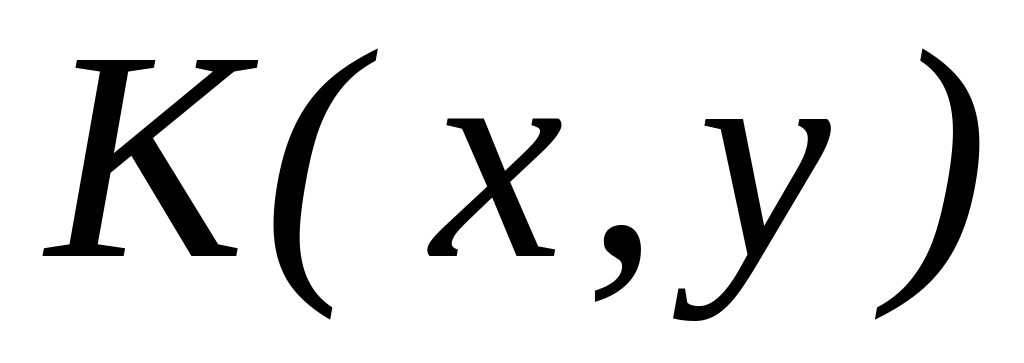 ,
,
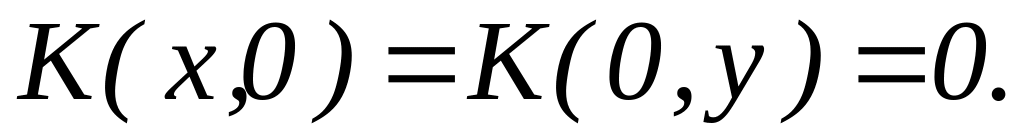
Наибольший общий делитель двух чисел,
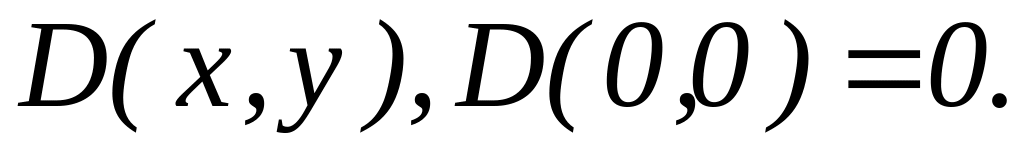
Целая часть от деления на ,
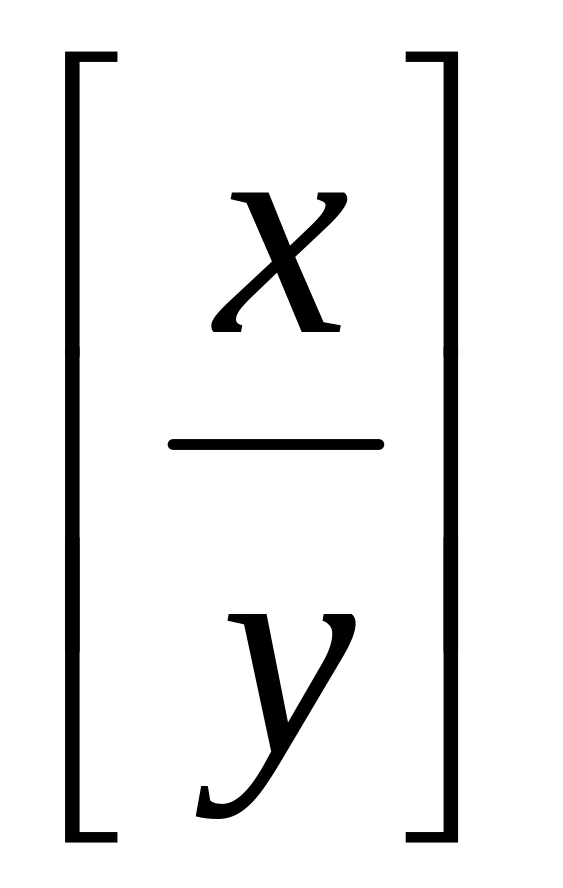 или
или
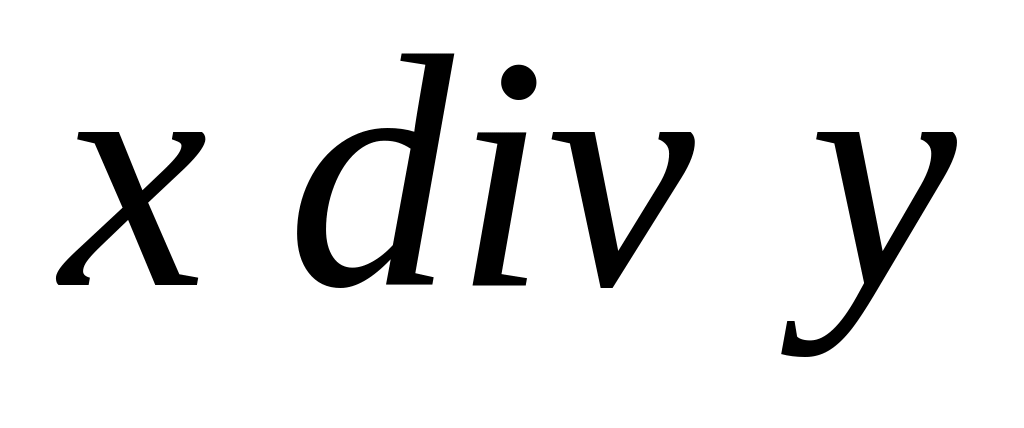 .
.Остаток от деления на ,

“Ступенька”:
 .
.Функция, отличная от нуля в конечном числе точек.
Номер наибольшего простого делителя числа
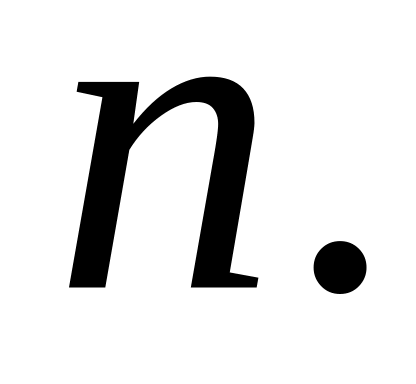
Функция
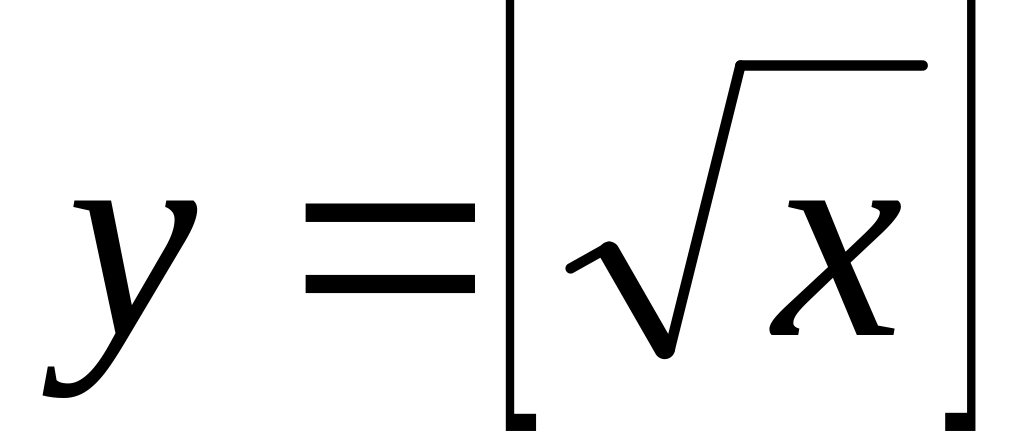 .
.
Варианты заданий к заданию 2.1
1. Реализовать функцию арифметическое
вычитание
![]() в
унарном коде.
в
унарном коде.
2. Реализовать функцию выбор максимального
из двух чисел
![]() над числами в унарном коде.
над числами в унарном коде.
3. Реализовать функцию
![]() над числами в унарном коде.
над числами в унарном коде.
