- •Антенно – фидерные устройства.
- •С хема радиолиний.
- •Классификация антенн.
- •Основные типы антенн.
- •Элементарные излучатели электромагнитных волн.
- •Понятие о магнитном токе.
- •Элементарный щелевой излучатель.
- •Элементарный излучатель гюйгенса.
- •Передающие антенны и их параметры.
- •1.5. Дн "ненаправленных" антенн.
- •1.6. Дн остронаправленных антенн.
- •1.7. Фазовые диаграммы антенны.
- •- Волновое число.
- •Коэффициент согласования передающей антенны.
- •Действующая длина передающей антенны.
- •Коэффициент направленного действия и коэффициент усиления передающей антенны.
- •Поляризационные характеристики передающей антенны.
- •Приемные антенны.
- •Эквивалентная схема приемной антенны.
- •2. Режим сильного сигнала в радиолиниях свч.
- •Симметричные вибраторы
- •Распределение тока на симметричном вибраторе
- •Симметричный вибратор с емкостной нагрузкой на концах
- •Распределение напряжения по симметричному вибратору
- •Поле излучения симметричного вибратора
- •Резонансная длина вибратора
- •Настройка в резонанс
- •Широкополосные вибраторы
- •Петлевой вибратор Пистолькорса
- •Питание симметричных вибраторов
- •Несимметричные антенны
- •Несимметричные антенны
- •Диско - конусная антенна
- •Влияние конечной проводимости земли
Действующая длина передающей антенны.
Выражение для напряжённости электрического поля в дальней зоне антенны с любым распределением тока вдоль ее оси может быть записано в таком же виде, как и для диполя Герца, имеющего равномерное распределение тока:
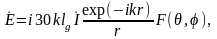
где
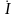 - комплексная амплитуда тока в некотором
сечении антенны;
- комплексная амплитуда тока в некотором
сечении антенны;
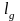 -
действующая длина антенны.
-
действующая длина антенны.
Таким образом, действительная длина любой антенны есть длина прямолинейной антенны с равномерный распределением тока, которая при одинаковых токах в отсчетных течениях создает в свободном пространстве такую же напряжённость поля в направлении максимального излучения, что и рассматриваемая антенна.
Отсюда находим макс. значение амплитуды напряженности электрического поля и действующую длину:
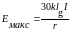 ,
, 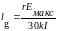
Как видно, действующая длина антенны с неравномерным распределением тока зависит от того, в каком сечении отсчитывается расчетный ток. Например, для действующей длины, отнесенной ко входу антенны, имеем:
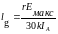
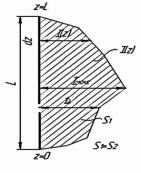
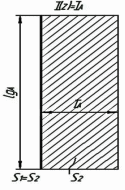
При известной напряженности электрического поля расчет действующей длины производится непосредственно с помощью формулы. Для прямолинейных антенн с синфазным распределением тока действующую длину можно определить с помощью понятия «площади тока». Как для диполя Герца, так и для любой антенны направленного поля пропорциональна произведению некоторой длины на ток, которое может быть использовано как площадь под графиком равномерного распределения тока с амплитудой I на длине Lg. Т.к. при синфазном распределении тока поля от всех участков провода в точке наблюдения, находящейся в дальней зоне, сложатся в фазе в направлении, перпендикулярном оси провода, то, считая каждый элементарный участок провода диполем Герца длиной dz с амплитудой тока I(z), для этого направления получаем:
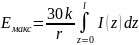
Интеграл в этом выражении представляет собой «площадь тока»
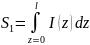
При условии равенства полей в направлении
максимального излучения данной антенны
и антенны с равномерным распределением
тока на длине их «площади тока» должны
быть равны, т.е.
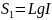 . Отсюда находим:
. Отсюда находим:
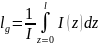
На рисунке показано определение действующей длины, отнесенной к току на входе антенны.
|
|
Коэффициент направленного действия и коэффициент усиления передающей антенны.
КНД передающей антенны определяется сравнением данной антенны с некоторой эталонной антенной, направленные свойства которой хорошо известны. В качестве эталонных широко используются: совершенно ненаправленный (изотропный) излучатель, диполь Герца, полуволновой вибратор. Предлагается, что КПД эталонных антенн равен 100%
КНД антенны в направлении
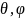
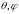 называется отношение
угловой плотности
называется отношение
угловой плотности 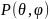 ,
создаваемой в этом направлении данной
антенной, к угловой плотности мощности
,
создаваемой в этом направлении данной
антенной, к угловой плотности мощности
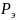 ,
создаваемой в этом же направлении
эталонной антенны, при условии равенства
полных мощностей излучения
рассматриваемой и эталонных антенн:
,
создаваемой в этом же направлении
эталонной антенны, при условии равенства
полных мощностей излучения
рассматриваемой и эталонных антенн:
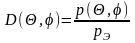 при
при
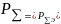
Другое определение, введенное А.А. Пистолькорсом: КНД антенны называется число, показывающее, во сколько раз нужно увеличить мощность излучения эталонной антенны для того, чтобы в заданном направлении получить одинаковые угловые плотности мощности, а следовательно, при одинаковых расстояниях - одинаковые напряженности поля:
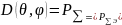
при
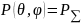 или
или
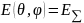 и
и
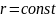
Из определения ДН по мощности следует, что
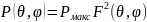
где
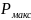 – угловая плотность мощности в
направлении максимума излучения,
– угловая плотность мощности в
направлении максимума излучения,
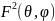 - нормированная ДН по мощности.
- нормированная ДН по мощности.
Учитывая это, получаем:
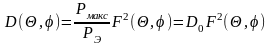
где
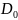 – КНД в направлении
излучения данной антенны. Таким образом,
КНД зависит от угловых координат и эта
зависимость определяется ДН антенны
по мощности. Сравнивая антенны,
сравнивают их КНД, то обычно имеют в
виду
– КНД в направлении
излучения данной антенны. Таким образом,
КНД зависит от угловых координат и эта
зависимость определяется ДН антенны
по мощности. Сравнивая антенны,
сравнивают их КНД, то обычно имеют в
виду
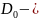 макс,
значения КНД.
макс,
значения КНД.
Коэффициент усиления антенны (КУ) определяется так же, как и КНД, только сравниваются не мощности излучения, а мощности, подводимые к антеннам. Для эталона антенны мощность излучения и подводимая мощность равны, т.к. ее КПД принят равным 100%. Реальные антенны имеют потери и их мощность излучения меньше подводимой мощности, на величину потерь.
Выражение для
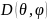 применительно к КУ имеет вид:
применительно к КУ имеет вид:
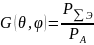 при
при
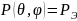
Т.к.
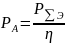 то
то
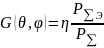
Для направления максимума ДН:
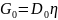
Пересчет КНД при переходе от одной эталонной антенны к другой часто требуется на практике и выглядит как:
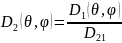
где
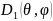 - КНД
антенны по отношению к первому эталону,
- КНД
антенны по отношению к первому эталону,
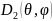 - ко
второму эталону,
- ко
второму эталону,
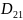 – КНД второго
эталона по отношению к первому.
Т.к. для эталонных антенн используется
отсчет КНД только в максимуме их
ДН, то величина
не зависит от угловых координат.
– КНД второго
эталона по отношению к первому.
Т.к. для эталонных антенн используется
отсчет КНД только в максимуме их
ДН, то величина
не зависит от угловых координат.
Расчет КНД часто выполняется по известному полю антенны в дальней зоне, хотя могут быть использованы и другие методы.
Положим, что антенна помещена в начале
сферической системы координат и находится
в свободном
пространстве. Антенна излучает поле
линейной поляризации и амплитуда этого
поля известна во всех точках поверхности
сферы радиуса
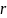 , т.е. известна ДН по полю
, т.е. известна ДН по полю
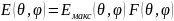 .
.
В
качестве
эталона возьмем изотропную антенну.
Угловая плотность мощности для нее:
(телесный угол для сферы равен
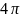 )
)
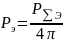
Из условия
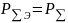 ,
воспользовавшись формулой для мощности
излучения антенн:
,
воспользовавшись формулой для мощности
излучения антенн:
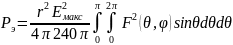
т.к.
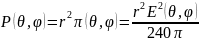 , а
, а
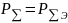 ,
получим
,
получим
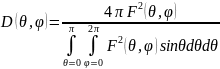
В направлении максим. излучения
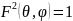 ,
поэтому:
,
поэтому:
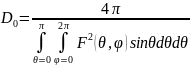
Отсюда следует, что. КНД однозначно определяется нормированной ДН, что существенно упрощает многие расчеты.
КНД элементарных
излучателей по отношению к изотропному
излучателю.
Нормированная ДН диполя Герца имеет
вид
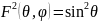 .
Подставляя
это выражение
в предыдущую формулу имеем:
.
Подставляя
это выражение
в предыдущую формулу имеем:
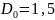 .
.
Для излучателя Гюйгенса ДН по модулю
электрического вектора записывается
в виде
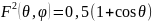 Отсюда, после интегрирования – D0
= 3.
Отсюда, после интегрирования – D0
= 3.