Понятие о магнитном токе.

Рассмотрим картину распределения магнитных силовых линий, получающуюся при протекании постоянного электрического тока I^э по проводящей бесконечной полос­ке нулевой толщины и ширины Δ в направлении, указанной стрел­кой.

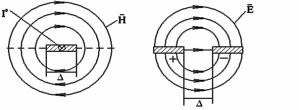
В непосредственной близости от проводника магнитные силовые линии будут в значительной степени повторять его контур, а на самой по­верхности проводника магнитный вектор будет тангенциален к плоскости полоски, отмеченной пунктиром. При удалении, силовые линии дефор­мируясь переходят в окружности.

Отметим следующий важный факт - в силу симметрии задачи, си­ловые линии магнитного поля подходят к плоскости в которой лежит про­водник, по направлению нормали всюду, за исключением полоски ши­риной Δ , занятой проводником. Другими словами, в пределах вы­деленной плоскости: Нτ = 0 вне проводника; Нτ ≠ 0 на проводнике.

Изучим теперь картину электрических силовых линий, в системе из двух заряженных металлических полуплоскостей, разделенных зазором шириной Δ. С точностью до направления стрелок в верхнем и нижнем полупространствах она оказывается тождественной той, которая рассматривалась ранее, причем: Еτ = 0 вне зазора, Еτ ≠ 0 в зазоре.

Указанное сходство в картинах распределения полей позволяет чисто формально, предполагать, что в щели по направлению, параллельно ее кромкам, протекает некоторый гипотетический ток I^M , называе­мый магнитным током, (магнитных носителей не существует, поэтому дан­ная величина играет вспомогательный характер. Направление магнитного тока принято определять противоположным тому, которое взято для электрического тока).

Элементарный щелевой излучатель.

Данная излучающая система представляет собой бесконечную металлическую плоскость, в которой прорезана щель длиной L и шириной Δ. Для возбуждения в щели переменного магнитного тока могут быть использованы различные способы. Так источник высокочастного напряжения может быть подключен к обеим кромкам щели. При этом получается двухсто­роннее возбуждение щели, поскольку электромагнитная энергия излучается в оба полупространства. На практике часто применяют одностороннее воз­буждение щелевого излучателя, например, с помощью прямоугольного волновода с волной H₁₀. Здесь переменные электронные заряды на кромках щели наводятся за счет протекания поверхностных электрических токов по участ­ку плоскости, закорачивающий волновод.

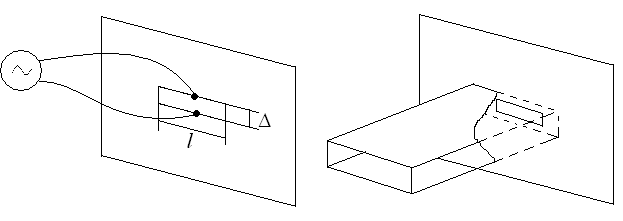
Для того, чтобы рассматриваемая щель могла считаться элементарным излучате­лем, необходимо выполнение условия l <<λ при этом обыч­но Δ<<l .

Случай двухстороннего возбуждения щелевого излучателя - при­меним принцип перестановочной двойственности к известным составляющим поля элементарного электрического излучателя выпишем составляющие поля справедливые в дальней зоне:

- для электрического излучателя:

.

.

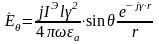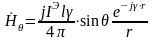- для щелевого, излучателя:

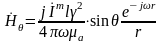
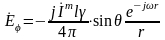
То, что элементарный щелевой излучатель в дальней зоне имеет единс­твенную составляющую электрического вектора, направленную по сферической коорди­нате φ, говорит о том, что силовые линии электрического поля, выходя из щели, приобретают на некотором удалении форму окружностей.

На практике в качестве величины, характеризующей интенсив­ность источника, гораздо удобнее использовать не амплитуда стороннего магнитного тока I^M, а напряжение, в щели U_щ , измеряемое в вольтах.

Тангенсальная составляющая магнитного поля на поверхности проводящей полоски ис­ходя из закона полного тока:

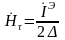
предполагается, что полоска нулевой толщины

Полагая, что напряженность электрического поля в зазоре щели постоянна, имеем:

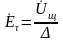
в силу перестановочной двойственности:

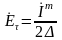
Откуда:

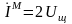
что позволяет записать окончательные выражения для составляющих электромагнитного поля щелевого излучателя в дальней зоне:

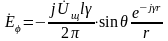
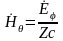
Среднее значение вектора П. имеет единственную составляющую, направленную по координате r :

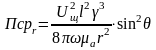
откуда непосредственно может быть вычислена излучаемая мощность:

;

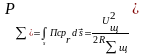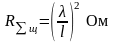
Сравним эффективности рассмотренных, видов элементарных излучателей. Пусть имеются два совершенно одинаковых по конфигурации излучателя, один из которых электрический, а другой – щелевой. Пусть по электронному излучателю протекает ток I , Каково должно быть напряжение U_щ , для того, чтобы излучаемые мощности совпадали? Т.е. должно выполняться равенство:

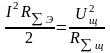
Пусть ток I=1 А. Тогда из формул имеем: U_щ=188 В. Данный результат говорит о недостатке щелевого излучателя, пос­кольку напряжение в щели существенным образом ограничено, возмож­ностью электрического пробоя.

Существуют и другие излучающие системы, поле которых сходно с конфигурацией поля щелевого излучателя - излучатель в виде дос­таточно малой проволочной петли, по которой протекает переменный электрический ток с амплитудой I^э . Здесь можно предположить, что в направ­лении, перпендикулярном плоскости петли, протекает сторонний магнит­ный ток I^м . По этой причине достаточно малые щелевой и рамоч­ный излучатели могут быть отнесены к классу элементарных магнитных излучателей.

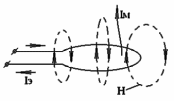
(H-направлен в другую сторону)