Симметричный вибратор с емкостной нагрузкой на концах

Емкостная нагрузка выполняется в виде диска или системы проводов, перпендикулярных оси вибратора и используется при необходимости уменьшить длину вибратора с сохранением его основных характеристик излучения. Токи, текущие по проводам концевой час­ти, практически не участвуют в излучении, однако, при емкостной нагрузке ток на конце вибратора отличен от нуля. На рис. (ж) пока­зано распределение тока по вибратору длиной с нагрузкой на конце - здесь распределение тока на участке между клеммами и кон­цевой нагрузкой такое же, как у вибратора длиной без нагрузки. Концевая нагрузка как бы "удлиняет" вибратор. При ее эффект в отношения распределения тока по вибратору такой же, как и эффект подключения емкости к концу разомкнутой двухпровод­ной линии ("емкостная нагрузка").

Распределение тока для этого случая описывается выражением:

где - кажущееся приращение длины вибратора – эквивалентная длина емкостной (концевой) нагрузки.

Распределение напряжения по симметричному вибратору

Напряжение в симметричном вибраторе определяется как разность потенциалов в симметричных относительно середины участках . Если вибратор имеет значительную электрическую длину , то электрические процессы в пространстве вокруг вибратора будут иметь волновой характер и понятие напряжения теряет смысл (из-за разности рас­стояний от излучателя до проводов фазы наводимых ЭДС в проводах будут заметно различаться - результирующая ЭДС в контуре будет отлична от нуля).

Для коротких вибраторов поле вблизи вибратора - по­тенциальное, как в поперечном сечении двухпроводной линии, и рас­пределение напряжения аналогичное двухпроводной линии .

Для вибраторов большой длины – определяется напряженность нормальной к поверхности вибратора составляющей электрического поля, которая пропорциональна поверхностной плотности заряда (рис.). Наиболее опасными с точки зрения эл. пробоя являются участки вибратора вблизи пучностей или максимумов распределения заряда.

Поле излучения симметричного вибратора

Напряжение электрического поля, создаваемого симметричным вибратором в некоторой точке М окружающего пространства, может быть определена как векторная сумма полей, создаваемых в этой точке всеми бесконечно малыми участками вибратора длиной . Т.к. длина участка может быть сколь угодно малой, то распределение тока на этом участке можно считать равномерным, т.е. сим­метричный вибратор можно считать состоящим из непрерывно распреде­ленных диполей Герца длиной .

М – элементарное поле – сумма симметричных участков ,

- в дальней зоне.

Напряженность поля, создаваемую вибратором в точке М, можно найти интегрированием по всем элементам:

- величина поля и его зависимость от полярного угла определяются распределением комплексных амплитуд тока по вибратору и длиной вибратора.

Прямолинейный вибратор имеет только меридиональную составляющую электрического поля , поэтому магнитное поле имеет только составляющую (волновое сопротивление среды).

Величина интеграла слабо зависит от вида функции , поэтому действительное распределение тока можно заменить синусоидальным:

Тогда:

Симметричный вибратор имеет фазовый центр, расположенный в сере­дине вибратора (фаза поля не зависит от угловых координат, а мно­житель описывает сферическую волну).

Вычисление интеграла производится заменой произведения тригонометрических функций их суммой; получаем:

,

где - ток в антенне.

Диаграмма направленности симметричного вибратора

ДН определяется множителем в выражении для амплитуды поля Е , зависящим от угла

Нормированная ДН получается умножением на нормирующий множитель, равный величине, обратной . При ДН имеет один максимум, перпендикулярный оси. Для этого случая ( ), имеем: . Нормированная ДН запишется в виде:

, при .

При , необходимо определить направление максимального излучения и затем вычислить нормирующий множитель.

Пространственные ДН получаются вращением этих кривых вокруг оси z. При увеличении ДН сужаются. Однако уже при в ДН появ­ляются побочные лепестки, затем главный лепесток расщепляется на несколько. Чем больше ( ), тем уже каждый лепесток и тем больше их число. Короткие вибраторы ( ) имеют такую же ДН, как и ди­поль Герца.

Для полуволнового вибратора ( ) ненормированная и нормированная ДН совпадают:

.

Действующая длина симметричного вибратора

Для вибраторов с одним максимумом ДН действующая длина, от­несенная ко входу антенны, равна:

,

или:

Напряженность электрического поля в максимуме ДН рассчитывается через дейст­вующую длину по формуле:

.

Действующая длина полуволнового вибратора одинакова при отс­чете как к току в пучности, так и к току на входе, т.к. пучность тока совпадает со входными клеммами: .

Для коротких вибраторов ( ): ,

- половина геометрической длины.

Сопротивление излучения симметричного вибратора рассчитывается по известному полю в дальней зоне. Отметим две характерные точки: для

полу­волнового вибратора ( ): Ом, а для волнового : Ом.

Входное сопротивление симметричного вибратора

В случае тонких вибраторов оно определяется через известные напряжение и ток на входе, в случае не очень тонких вибраторов обычно пользуются экспериментальными данными. Рассмотрим экспериментальные кривые зависимости R_A и X_A составляющих входные сопротивления цилиндрического симметричного вибратора для разных относительных диаметров.

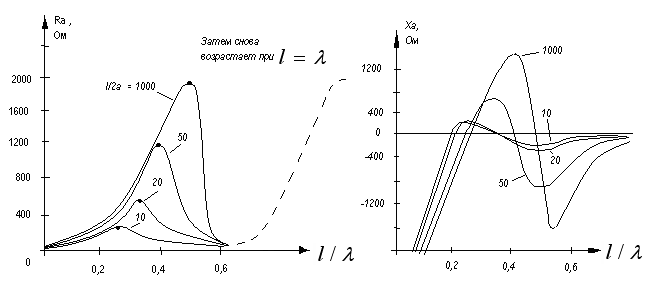
При активное сопротивление мало зависит от толщины вибратора и с увеличением частоты монотонно растет, достигает максимума и снова уменьшается. Положение максимумов R_A сильно зависит от толщины вибратора: для очень тонких - максимум достигается при длинах l, близких к nλ/2 , где n - целое число. Т.е. большое значение R_A будут иметь вибраторы длиной 2l ≈ λ, 2λ, 3λ,..... Чем толще вибратор, тем при меньших λ/l достигается максимум R_A и тем меньше его ве­личина. Если зафиксировать длину вибратора и менять рабочую часто­ту (длину волны), то окажется, что более толстые вибраторы будут диапазонными, т.к. их входное сопротивление меняется более плавно, чем у тонких.

Реактивная составляющая также изменяется в очень широких пределах. Увели­чение толщины вибратора сглаживает кривую X_A(l/λ).

С увеличением длины вибратора максимумы реактивной составляющей X_A входного сопротивления уменьшаются, а максимумы и минимумы акт. сост. сближаются, стремясь к величине волнового сопротивления вибратора W_B. Когда длина каждого плеча вибратора станет больше десятка длин волн, входное сопротивление будет активным, близким к величине W_B.