Контрольные вопросы

1. Что называется моментом инерции тела?

2. Запишите основное уравнение динамики вращательного движения и уравнение моментов.

3. Что называется тензором инерции?

4. Что такое главные и центробежные моменты инерции?

5. Что такое эллипсоид инерции?

6. Получите формулы для моментов инерции диска и цилиндра относительно их геометрических осей.

7. Запишите выражение для кинетической энергии тела, участвующего в поступательном и вращательном движении.

8. Сформулируйте теорему Гюйгенса-Штейнера.

Контрольные вопросы

1.Момент инерции твердого тела - скалярная физическая величина, характеризующая распределение масс в теле, равная сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости)

2. Запишите основное уравнение динамики вращательного движения и уравнение моментов.

M=Jε, M-вращающий момент - уравнение динамики вращательного движения

J=∑m_id²_i - уравнение моментов

3. Что называется тензором инерции?

Совокупность величин

.

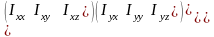называется тензором инерции.

Тензор инерции- важнейшее понятие, необходимое для выяснения движения около точки закрепления.

4. Что такое главные и центробежные моменты инерции?

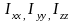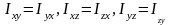Величины называются осевыми моментами инерции, а называются центробежными моментами инерции.

Центробежный момент инерции вычисляются как суммы произведений масс m_к точек тела (системы) на две из координат x_k, у_к, zk этих точек:

Значения Центробежный момент инерции зависят от направлений координатных осей. При этом для каждой точки тела существуют по крайней мере три такие взаимно перпендикулярные оси, называемые главными осями инерции, для которых Центробежный момент инерции равны нулю.

От значений Центробежный момент инерции зависят величины сил давления на подшипники, в которые закреплена ось вращающегося тела. Эти давления будут наименьшими (равны статическим), если ось вращения является главной осью инерции, проходящей через центр масс тела

5 Получите формулы для моментов инерции диска и цилиндра относительно их геометрических осей.

а)диск

dJ=dm_ir²_i , где m=ρV, V=2πrdr

J=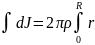 dr=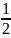 πr^{4 ,} т.к. πr²- объем диска, то m= πr²ρ, следовательно

J= mr²

б)цилиндр

разобьем на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним r+dr

V=2πrhdr- объем элементарного цилиндра

J=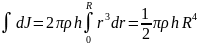 , т.к.h πR²-объем цилиндра, следовательно m= πR²hρ, тогда

J= mr^{2 .}

6. Запишите выражение для кинетической энергии тела, участвующего в поступательном и вращательном движении.

T_вр=Jω²/2 –для вращательного движения

T=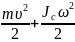 - для поступательного движения.

7. Сформулируйте теорему Гюйгенса-Штейнера.

Согласно этой теореме момент инерции тела относительно произвольной оси равен сумме момента инерции этого тела относительно оси проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела на квадрат расстояния между осями.

7