L-ичного
ДКС.
Рассчитаем
распределение вероятностей дискретного
сигнала на выходе детектора,
скорость
передачи информаии по L-ичному ДКС,
относительные потери в скорости передачи
информации по L-ичному ДКС.
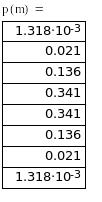
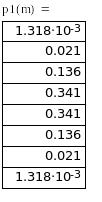
Распределение
вероятностей дискретного сигнала на
выходе детектора р1(m):
10. Рассмотрим отклик детектора пру как случайный дискретный сигнал на выходе
Энтропия
ошибочных решений =
Энтропия
восстановленного L-ичного сообщения =
Скорость
передачи информации по L-ичному ДКС =
Величина
относительный потерь в скорости =
Закон
распределения вероятностей отклика
декодера.
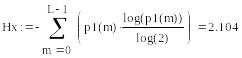
равной
начальной энергетической ширине спектра
исходного сообщения:
Рассчитать
дисперсию случайных импульсов шума
передачи на выходе интерполятора ЦАП,
среднюю квадратическую погрешность
шума передачи,
суммарную
начальную СКП восстановления непрерывного
сообщения,
отсносительную
СКП.
Дисперсия
случайных импульсов шума передачи на
выходе интерполятора:
Ввиду
того, что поогрешность фильтрации, шум
квантования и
шум
передачи - независимые случайные
процессы, то суммарная СКП восстановления
непрерывного сообщения будет равна
сумме указанных процессов
Отсносительная
суммарная СКП восстановленного сообщения
=
11. Полагаем фнч на выходе цап приемника идеальным с полосой пропускания,
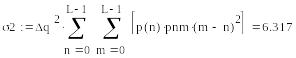
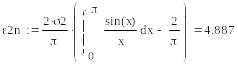
исходного
сообщения не приводит к минимуму ОСКП,
решим
оптимизационную
задачу: определим оптимальную
энергетическую ширину
спектра
сообщения, доставляющую минимум
относительной суммарной
СКП
его восстановления.
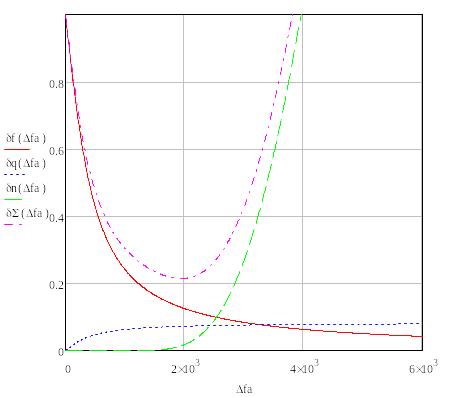
12. В виду того, что выбор начальной энергетической ширины спектра
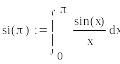
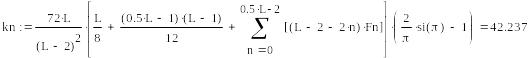
Относительные
СКП фильтрации, квантования и передачи
зависят от энергетической ширины
спектра сообщения различным образом:
Суммарная
величина относительной СКП имеет
минимум при оптимально
выбраанной
энергетической ширине спектр исходного
сообщения, равной 1.941 кГц.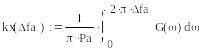
Московский Технический Университет Связи и Информатики.
Курсовая работа по Теории Электрической Связи.
(3 курс,5 семестр)
Выполнил студент гр. СС0702 Прошкин Д.И.
Проверил преподаватель Потапова Е.А.
Вариант 19.
Москва 2009.
Задание:
