Министерство образования Республики Беларусь

Учреждение образования

«Белорусский государственный университет

информатики и радиоэлектроники»

Кафедра систем телекоммуникаций

КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Направляющие системы

телекоммуникаций»

Вариант 311

Минск 2011г.

ВАРИАНТ 311

Задача №1

Определить первичные и вторичные параметры передачи симметричного кабеля.

Найти также их составляющие: R₀ – сопротивление по постоянному току; R_п.э – сопротивление за счёт поверхностного эффекта; R_бл – сопротивление за счёт эффекта близости; L_мп – межпроводниковую индуктивность; L_вп – внутрипроводниковую индуктивность; α_м – затухание за счёт потерь в металле; α_д – затухание за счёт потерь в диэлектрике.

Параметры кабеля представлены в таблице 1.

Таблица 1.

Изоляция	Толщина изоляции, мм	εэф	Частота f, кГц	tgδ·10-4	Скрутка	Расчетный диаметр	Материал проводника	Диаметр проводника, мм
Полиэтиленовая	0,32	1,9…2,1	10	2	Парная dп	1,71· d1	Медь	0,32

Решение:

Первичными параметрами симметричного кабеля являются:

R – активное сопротивление симметричной кабельной цепи переменному току;

L – индуктивность цепи;

С – ёмкость кабельной цепи;

G – проводимость изоляции кабельной цепи.

Уравнение для расчёта сопротивления симметричного кабеля имеет вид ([1], 5.64]):

R = R_п.т + R_п.э + R_бл (1.1)

где R_п.т = 2R₀ – сопротивление постоянному току;

R_п.э = 2R₀F(kr) – сопротивление за счёт поверхностного эффекта;

R_бл = 2R₀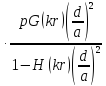сопротивление за счёт эффекта близости;

R₀ – активное сопротивление проводника;

χ – коэффициент укрутки проводов кабеля;

k – коэффициент потерь для металла;

r – радиус голого проводника;

р – коэффициент, учитывающий вид скрутки (при парной скрутке р=1);

F(kr), G(kr), H(kr) - специальные функции, полученные с использованием видоизменённых функций Бесселя;

d – диаметр голого проводника;

а – расстояние между центрами проводников.

Сопротивление прямого провода определим по формуле ([2], 1.4]):

R₀ = ,

где ρ = 0,0175 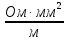– удельное сопротивление меди при t=20°C.

Тогда

R₀ = 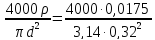= 217,6 (Ом)

Коэффициент укрутки проводов кабеля характеризует удлинение жил относительно длины кабеля. Так как структура кабеля не определена условием задачи в полной мере, выберем повивную систему скрутки групп в сердечник кабеля, в центральном повиве – 1 группа. Будем рассматривать симметричную кабельную цепь, расположенную в третьем повиве.

Диаметр изолированного проводника равен:

d₁ = d + 2∆ = 0,32 + 2 · 0,32 = 0,96 (мм)

Диаметр центрального повива определим по формуле:

D₀ = 2d₁ = 2 · 0,96 = 1,92 (мм)

Средняя толщина повива равна:

d_п = 1,71 · d₁ = 1,71 · 0,96 = 1,64 (мм)

Рассчитаем параметры цепи, находящейся в третьем повиве. Определим средний диаметр третьего повива:

D₃ = D₀ + 3d_п = 1,92 + 3 · 1,64 = 6,84 (мм)

Коэффициент укрутки проводов кабеля определяется выражением ([2], 1.1):

χ =

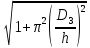
где h – шаг скрутки. Его величина обычно составляет 100…300 мм. Выберем h = 200 мм. Тогда:

χ = 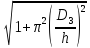= = 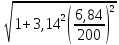1,0057

Теперь рассчитаем сопротивление цепи кабеля постоянному току ([2], 1.2):

R_п.т = 2R₀··1,0057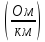

Коэффициент вихревых токов определим по формуле:

k = ,

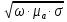где ω = 2πf = 2 · 3,14 · 10⁴ = 6,28 · 10⁴

μ_а = μ₀ · μ_r – абсолютная магнитная проницаемость;

μ₀ = 4π · 10^-4 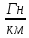– магнитная проницаемость вакуума;

μ_r = 1 – относительная магнитная проницаемость проводника (для медных и алюминиевых проводов μ_r = 1);

σ = 57,00 · 10^-3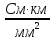 – удельная проводимость меди.

Тогда:

k = 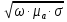= = = 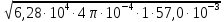2,12 (мм^-1)

Рассчитаем коэффициент kr (произведение коэффициента вихревых токов на радиус голого проводника):

kr = k = 2,12 = 0,339.

С помощью таблицы ([1], 5.1]) найдем значения специальных функций F(kr), G(kr), H(kr):

F(kr) = 0,0002,

G(kr) = 0,0006,

H(kr) = 0,042,

Q(kr) = 0,99999.

Определим сопротивление за счет поверхностного эффекта:

R_п.э = 2R₀F(kr) = R_п.т F(kr) = 

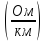
Определим сопротивление за счет эффекта близости:

R_бл = 2R₀R_п.т·437,5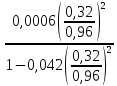·0,029

где а = d + 2∆ = 0,32 + 2 · 0,32 = 0,96 (мм) – расстояние между проводниками.

Сопротивление кабельной цепи переменному току равно (1.1):

R = R_п.т + R_п.э + R_бл = 437,5 + 0,0875 + 0,029 = 437,6 .

Индуктивность цепи в целом определяется суммой внешней (межпроводниковой) L_мп и внутренней (внутрипроводниковой) L_вп = 2L_а индуктивностей:

L = L_мп + L_вп = L_мп + 2L_а (1.2)

Межпроводниковая индуктивность определяется выражением ([2], 1.7]):

L_мп =  6,4  10^-4

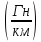
Внутрипроводниковая индуктивность равна:

L_вп = μ_r  Q(kr)  10^-4 = 1  0,9999  10^-4 = 9,99  10^-5

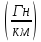
Общая индуктивность симметричной кабельной цепи равна (1.2):

L = L_мп + L_вп = 6,4  10^-4 + 9,99  10^-5 = 7,39  10^-4 .

Емкость симметричной кабельной цепи с учетом близости соседних пар определяется выражением ([1], 5.68]):

С = ,

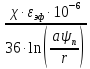
где ε_эф = 1,35 – эффективная диэлектрическая проницаемость изоляции;

Ψ_п – поправочный коэффициент, характеризующий близость соседних пар:

Ψ_п = 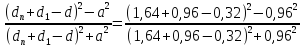= 0,699.

Подставляя данные значения, получаем:

С = = 2,62  10^-8

Проводимость изоляции G характеризует потери энергии в изоляции проводов кабеля. Величина проводимости определяется выражением ([1], 5.69]):

G = G₀ + G_f = + Сtg,

где G₀ – проводимость изоляции по постоянному току,

G_f – проводимость изоляции по переменному току,

С – емкость симметричной цепи,

tg  - тангенс угла диэлектрических потерь.

Для кабельных симметричных цепей величина G₀ = очень мала по сравнению с G_f, и ей можно пренебречь. Тогда:

G  Сtg = 6,28 · 10⁴  2,62  10^-8  2  10^-4 = 3,29  10^-7

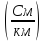
Вторичные параметры симметричной цепи являются:

Z_в – волновое сопротивление;

 – коэффициент затухания;

 – коэффициент фазы;

V – скорость распространения энергии.

Волновое сопротивление определяется по формуле ([1], стр. 171]):

Z_в = = = 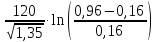165,25 .

Коэффициент затухания равен сумме двух составляющих ([1], стр. 171]):

 = _м + _д,

где _м – коэффициент затухания в металле,

_д – коэффициент затухания в диэлектрике.

_м = 0,5  R 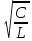= 218,8  = 1,3

_д = 0,5  G 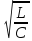= 1,65  10^-7 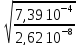 = 2,77  10^-5

Суммарный коэффициент затухания:

 = _м + _д = 1,3 + 2,77  10^-5 = 1,3

Коэффициент фазы определяет угол поворота вектора тока на протяжении одного километра и на низких частотах определяется:

 = 2    f  = 6,28 · 10⁴ 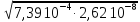 = 0,28

Скорость распространения электромагнитной энергии является функцией частоты и фазовой постоянно, которая в свою очередь зависит от первичных параметров линии. В общем виде она определяется по формуле:

V = = = 2,27 10⁵ .

Задача 2

Определить первичные и вторичные параметры передачи коаксиального кабеля.

Параметры кабеля представлены в таблице 2.

Таблица 2.

Изоляция	εэф	Частота f, МГц	tgδ·10-4	Материал проводника	Диаметры внутреннего и внешнего проводников, мм
Балонно- полиэтиленовая	1,22	1	0,5	Медь/медь	2,6/9,5

Решение.

При расчёте на частотах более 60 кГц сопротивление коаксиального кабеля в основном определяется суммой сопротивлений внутреннего проводника R_a и внешнего проводника R_b и определяется по формуле ([1], 5.29):

R = R_a + R_b = 4,18 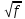   10^-2,

где r_a = d_a/2 = 1,3 (мм)

r_b = d_b/2 = 4,75 (мм)

R = R_a + R_b = 4,18 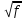   10^-2 = 4,18    10^-2 = 40,97 .

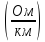Индуктивность коаксиального кабеля состоит из суммы внутренней индуктивности внутреннего проводника L_a и внешнего проводника L_b и наружной межпроводниковой индуктивности L . На низких частотах определяется по упрощённой формуле ([1], 5.32):

L = L_a + L_b + L_мп =  10^-4 = 2,65  10^-4 .

Значение ёмкости коаксиальной пары определим по формуле:

С = 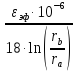= = 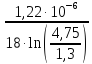5,24  10^-8.

Расчёт проводимости проводим по формуле ([1], 5.36) при допущении, что сопротивление изоляции постоянному току бесконечно большое. Тогда

G  Сtg = 2  f  С  tg = 2  3,14  1  10⁶  5,24 10^-8  0,5  10^-4 = 1,6  10^-5 .

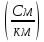При расчётах вторичных параметров учтём, что коаксиальные кабели практически используются на частотах более 60 кГц, где R<<ωL и G<<ωC, поэтому вторичные параметры обычно рассчитываются по упрощённым формулам.

При работе на частоте от 2 МГц для среды с μ_r=1 волновое сопротивление можно определить из выражения ([1], 5.41)

Z_в = 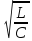= = 71,1 (Ом).

Коэффициент затухания [1], 5.37:

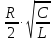
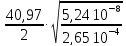
_м =  8,69 =  8,69 = 2,5

Потери в диэлектрике равны:

_д =  8,69 = 4,94  10^-3

Суммарные потери в кабеле равны:

 = _м + _д = 2,5 + 4,94  10^-3 = 2,5

Коэффициент фазы определяет угол сдвига между током (или напряжением) на протяжении одного километра

 = 2    f 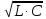 = 6,28 · 10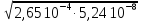⁴  = 23,4

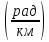
В области высоких частот, скорость распространения энергии практически не зависит от частоты и определяется по формуле [1], 5.39:

V = = = 2,68 10⁵ .

Задача 3

Определить параметры передачи: критическую частоту, критическую длину волны, волновое сопротивление, затухание, фазовую и групповую скорости, коэффициент фазы цилиндрического волновода с параметрами, приведёнными в таблице 3.

Таблица 3.

Диаметр волновода, см	Вид моды	Частота f, ГГц	Материал проводника	  107,
7	Е01	24	Медь	5,7

Решение.

Критическая длина волны определяется выражением ([1], 5.101)

₀ = ,

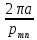где р_mn – корни, при которых функции Бесселя имеют нулевые значения;

m – индекс, указывающий на принадлежность корня к функции Бесселя порядка m;

n – порядковый номер корня;

a – радиус волновода.

Для типа волны Е₀₁ значение p₀₁=2,405.

Тогда

₀ = 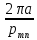= = 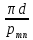= 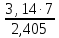9,14 (см) = 0,091 (м)

Критическая частота равна:

f₀ = = = 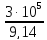3,28  10⁹ (Гц)

где с = 310⁵ – скорость света в вакууме.

Циклическая частота равна:

 = 2f = 2  3,14  24  10⁹ = 1,51  10¹¹

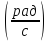
Считая, что волновод заполнен воздухом (_r = 1, ε_r = 1) волновое число среды распространения равно

k = 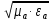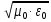 = = 1,5110¹¹= 1,5110¹¹= ·10⁸ = 502,65

Коэффициент фазы равен ([1], 5.101)

 = k

Обозначим

h = 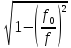= = 0,99.

Тогда

 = k 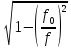= k  h = 502,65 · 0,99 = 497,93

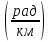
Фазовая скорость определяется по выражению ([1], 5.103)

V_ф = 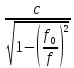= = = 3,03  10⁵

Групповая скорость определяется по выражению ([1], 5.104)

V_гр = с = сh = 310⁵  0,99 = 2,97  10⁵

Волновое сопротивление заполняющего волновод диэлектрика равно:

Z_а = = = 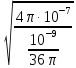= 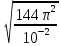376,99 (Ом)

Волновое сопротивление для волны Е-типа определим по выражению ([1], 5.105)

= Z_а = Z_а  h = 376,99 · 0,99 = 373,2 (Ом)

Активная часть волнового сопротивления металла стенок волновода равна:

Z_м.а = 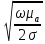= = 0,04 (Ом)

Коэффициент затухания для волны Е-типа равен ([1], 5.106)

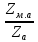
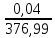
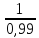
^E =  8,67 =   8,67 = 9  10^-4