4 Вывод передаточной функции фильтра по структуре Саллена-Кея

Структура фильтрового звена второго порядка на источнике напряжения управляемого напряжением (Саллена-Кея) представлена на рисунке 2.

Рисунок 4.1 – Структура Саллена-Кея для фильтрового звена второго порядка

Считая, что операционный усилитель идеален, потенциал узла А обозначим , а потенциалы на входах операционного усилителя соответственнои, причем. По первому закону Кирхгофа запишем

(4.1)

Выражая токи по закону Ома через потенциалы и проводимости и учитывая третье и второе уравнения из (36), получаем ,. Следовательно,. Первое уравнение из (16) преобразуется к виду

, (4.2)

последнее позволяет представить передаточную функцию цепи

. (4.3)

Сравним (4) с операторной передаточной функцией фильтра верхних частот второго порядка с аппроксимацией частотных характеристик Чебышева (Получен из ФНЧ преобразованием p=1/p)

. (4.4)

устанавливаем ,,,,,(рисунок 4.2).

Рисунок 4.2 – Фильтр верхних частот второго порядка с аппроксимацией Чебышева (Баттерворта) по структуре Саллена-Кея

Получим

. (4.5)

Сравнивая (4.4) и (4.5), имеем систему уравнений для расчета номиналов схемы

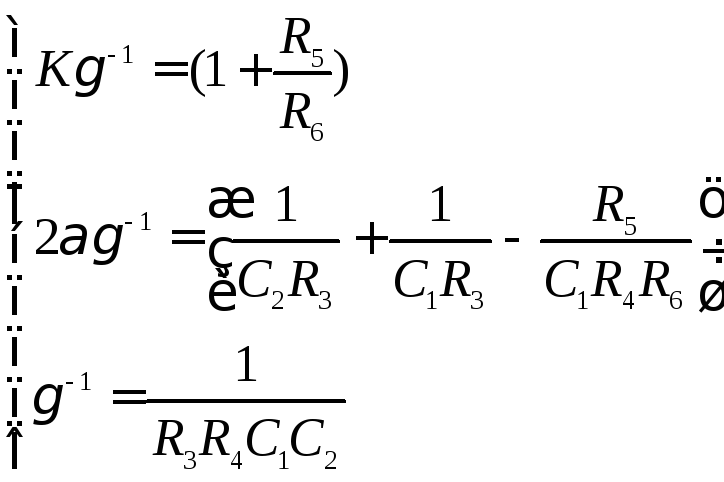(4.6)

При денормировании

(4.7)

и тогда (4.6) преобразуется к виду

(4.8)

Для реализации фильтра 9 порядка необходимо использовать 4 фильтра Саллена-Кея по структуре рассчитанной выше и 1 ФВЧ 1-го порядка (можно по той же структуре).

Передаточная функция активного звена ФВЧ 1-го порядка (получен из ФНЧ прототипа)

(4.9)

Такое звено можно организовать на основе структуры (рис 4.3)

Рисунок 4.3 – Структура для фильтрового звена первого порядка

Для схемы на рис 4.3 с делителем на входе получаем (R_k4=0)

(4.10)

При денормировании получим

(4.11)

Для устранения знака «-» в (14) можно использовать еще один инвертирующий ОУ с коэффициентом передачи -1. Таким образом

(4.12)

5 Моделирование фильтра на функциональном уровне в MathCad в частотной и временной областях (ачх, фчх, хрз,хгвз, их, пх) в нормированном и денормированном виде

Неравномерность затухания в полосе пропускания, исходя из заданной величины в % определим по формуле приведенной ниже. Также пересчитаем величину затухания (%) в параметр ε

Рассчитаем характеристики нормированного фильтра.

Характеристики фильтра получаем из общей передаточной функции (p=iw, заметим, что в зарубежной системе обозначений оператор р обозначается как s)

Амплитудно-частотная характеристика (АЧХ)

(5.1)

Фазочастотная характеристика (ФЧХ)

(5.2)

Характеристика рабочего затухания (ХРЗ)

, (5.3)

где параметр ε был определен ранее, полином Баттерворта (n=8) .

Характеристика группового времени задержки (ХГРЗ)

(5.4)

Импульсная характеристика (ИХ)

(5.5)

Переходная характеристика (ПХ)

(5.6)

Расчет в нормированном виде

При расчете используем параметр нормированной частоты Ω.

Импульсная и переходная характеристика приведены ниже

Расчет в денормированном виде

При расчете переходим к денормированной частоте

Импульсная и переходная характеристика приведены ниже.

Видим, что результаты моделирования соответствуют заданным параметрам на курсовое проектирование.