Рекурсия является важным инструментом решения вычислительных математических задач. Она широко используется для определения синтаксиса языков программирования, а также в структурах данных при разработке алгоритмов сортировки и поиска для списков и деревьев. Математики применяют рекурсию в комбинаторике для разного рода подсчетов и вычислен] вероятностей. Рекурсия – важный раздел, имеющий теоретическое и практическое применение в общей теории алгоритмов, моделях исследования ог раций, теории игр и теории графов.

В данной главе мы даем общее введение в рекурсию и иллюстрируем применение различными приложениям. В следующих главах рекурсия будет использоваться для изучения деревьев и сортировки.

Понятие рекурсии

Для большинства людей рекурсивное мышление не является характерным Если вас, допустим, попросят определить степенную функцию х^п, где х -* действительное число, a n — неотрицательное целое, то типичным ответом будет следующий:

xⁿ=x´x´x´x´¼´x.

Функция S(n) вычисляет сумму первых n положительных целых — задача, которая решается путем многократного сложения.

S(n)=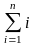

Рекурсия имеет место, когда вы решаете какую-то задачу посредством разбиения ее на меньшие подзадачи, выполняемые с помощью одного и того же алгоритма. Процесс разбиения завершается, когда мы достигаем простей­ших возможных решаемых подзадач. Мы называем эти задачи условиями останова. Рекурсия действует по принципу “разделяй и властвуй”.

Алгоритм определен рекурсивно, если это определение состоит из:

1. Одного или нескольких условий останова, которые могут быть вычислены для определенных параметров.

2. Шага рекурсии, в котором текущее значение в алгоритме может быть определено в терминах предыдущего значения. В конечном итоге шаг рекурсии должен приводить к условиям останова.

Например, рекурсивное определение степенной функции имеет единственное условие останова (n=0, т.к. х⁰ = 1). Шаг рекурсии описывает общий случай хⁿ = x´ х^n–1 при n>0.

Рекурсивные задачи

Сила рекурсии обеспечивает весьма простые и изящные решения ряда проблем. Приведем обзор задач и методов их решения, использующих рекурсию.

Ханойская башня. Любители головоломок долго были увлечены задачей о ханойской башне. Согласно легенде, у жрецов храма Брахмы есть медная платформа с троки алмазными шпилями. На одном шпиле А нанизано 64 золотых диска, каждый из которых немного меньше того, что под ним. Конец света наступит, когда жрецы переместят диски со шпиля А на шпиль С. Однако задача имеет весьма специфические условия. За один раз можно перемещать только один диск, при этом ни разу диск большего размера не должен лечь на диск меньшего размера. Несомненно, жрецы все еще работают, так как задача включает в себя 2⁶⁴–1 хода. Если тратить по одной секунде на ход, то потребуется 500 миллиардов лет.

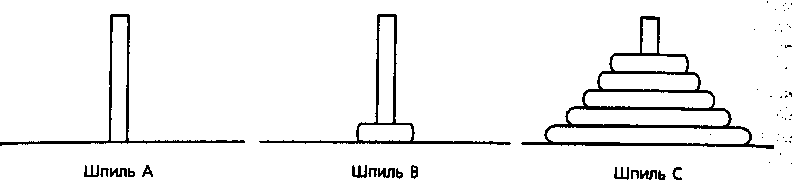
Ханойская башня — тяжелое испытание для решателя головоломок. Между тем опытный программист видит быстрое рекурсивное решение. Начнем, сосредоточившись на перемещении верхних n–1 дисков на шпиль B и последующего перемещения самого большого диска на шпиль C.

Осталась более простая задача перемещения только n–1 дисков со шпиля A на шпиль С. Применяя тот же самый алгоритм, сосредоточим внимание на верхних n–2 дисках и вытащим их из стопки. Затем перенесем самый большой диск со шпиля В на шпиль С. Осталась еще меньшая стопка дисков. Процесс продолжается до тех пор, пока не останется 1 диск, который, в конечном счете, перемещается на шпиль С.

Построение рекурсивных функций

Структура рекурсивной функции иллюстрируется задачей вычисления факториала неотрицательных целых чисел. Мы рассмотрим эту структуру, разработав как рекурсивное, так и итерационное определение функции.

Факториал неотрицательных целых чисел, Factorial(n), определяется как произведение всех положительных целых чисел, меньших или равных n. Число, обозначаемое n!, представляется следующим образом:

n!=n´(n–1)´(n–2)´¼´2´1.

Итерационная версия этой функции реализуется посредством возврата 1, если n=0, и циклом перемножения членов последовательности в противном случае

// итерационная форма факториала

long Factorial{long n)

{

int prod=1, i;

// для n==0 вернуть prod=i, в противном случае

// вычислить prod=1*2* *n

if {n>0)

for(i=1; i<=n; i++)

prod*=i;

return prod;

}

При вычислении n! нужно четко различать случай 0!, представляющий условие останова, и другие случаи (n>0), представляющие шаги рекурсии. Это различие является фундаментальным для построения рекурсивного алгоритма. Программист реализует распознавание данной ситуации с помощью оператора IF ... ELSE. Блок IF обрабатывает условие останова, а блок ELSE выполняет шаг рекурсии. Для факториала блок IF вычисляет единственное условие останова n=0 и возвращает единицу. Блок ELSE выполняет шаг рекурсии, вычисляя выражение n*(n–1)1, и возвращает результат.

// Рекурсивная форма факториала

long Factorial (long n)

{

// условием останова является n==0

if{n==0)

return 1;

else

// шаг рекурсии

return n*Factorial(n-1);

}

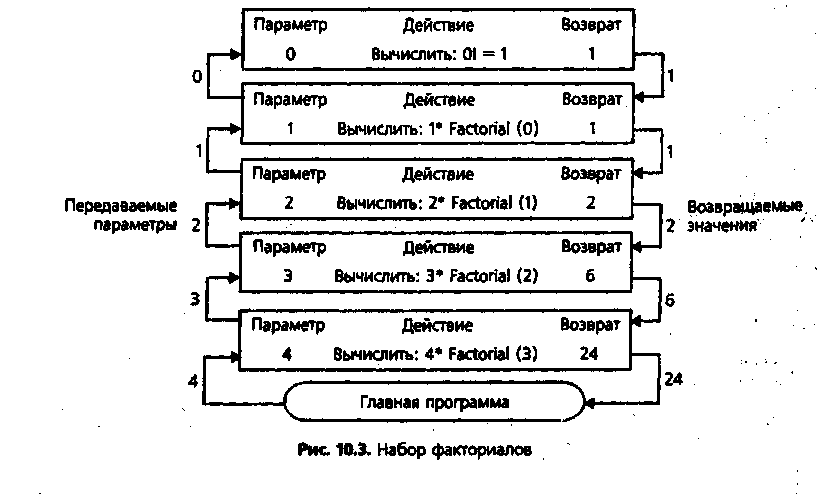
На рис. 2 описана последовательность вызовов функции при вычислении Factorial(4). Предположим, что первоначально функция вызывается из главной программы. Внутри блока функции выполняется оператор ELSE с параметрами 3, 2, 1 и 0. На последнем вызове выполняется оператор IF с n = 0. По достижении условия останова рекурсивная цепочка вызовов прерывается и начинается серия вычислений в порядке 1*1, 2*1, 3*2 и 4*6. Последнее значение 24 возвращается в главную программу.