
Алгоритмы и алгоритмическая сложность
.docxМинистерство образования Республики Беларусь
Белорусский государственный университет информатики и радиоэлектроники
Кафедра информационных технологий автоматизированных систем
Контрольная работа
по курсу
«Алгоритмы и алгоритмическая сложноать»
Выполнил:
студент группы 900621-16
Деркач А.Е.
Проверил:
Герман О.В.
Минск 2010
Контрольное задание №1
На вход поступает последовательность из 0 и 1. Машина должна заменить каждую единицу на 01. Пример. 00110010 заменяется на 00010100010.
Решение:
|
1 |
ε |
0 |
1 |
|
Q1 |
εUQfin |
0LQ1 |
0LQ2 |
|
Q2 |
1LQ1 |
|
|
ε – Пустой символ. Qfin – Конец работы машины Тьюринга.
Текст программы: unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls;
type
TForm1 = class(TForm)
Edit1: TEdit;
Memo1: TMemo;
Button1: TButton;
Button2: TButton;
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
i:integer;
stroka,itogstr: string;
implementation
{$R *.dfm}
procedure TForm1.Button1Click(Sender: TObject);
begin
Memo1.Clear;
stroka:=Edit1.text;
for i:=1 to length(form1.Edit1.text) do
begin
if stroka[i]='1' then
begin
Memo1.Lines.Add('01');
end else
begin Memo1.Lines.Add('0');
end;
end;
end;
procedure TForm1.Button2Click(Sender: TObject);
begin
itogstr:='';
Memo1.Clear;
stroka:=Edit1.text;
for i:=1 to length(form1.Edit1.text) do
begin
if stroka[i]='1' then
begin
itogstr:=itogstr+'01';
end else
itogstr:=itogstr+'0';
end;
Memo1.Lines.Add(itogstr);
end;
end.
При нажатии кнопки Button1 символы выводятся в столбик.
При нажатии Button2 символы выводятся в строку.
Контрольное задание №2
Решить задачу ВЫПОЛНИМОСТЬ Методом резолюций Робинсона.
Дизъюнкты
кодируются последовательностью чисел,
например, 1,-2,4,-6. Эта последовательность
задает следующий дизъюнкт:
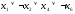 .
В Вашем варианте будет представлено
несколько дизъюнктов. Из п.А Вы выбираете
метод и применяете его к Вашей задаче
ВЫПОЛНИМОСТЬ. Вы должны показать работу
метода по шагам с разъяснением.
.
В Вашем варианте будет представлено
несколько дизъюнктов. Из п.А Вы выбираете
метод и применяете его к Вашей задаче
ВЫПОЛНИМОСТЬ. Вы должны показать работу
метода по шагам с разъяснением.
Вариант 4. -1,-2,-3
-2,3
3,5
3, -5
-3, -4
5,
4
Решение:
D1 =¬x1 v ¬x2 v ¬x3;
D2 =¬x2 v x3;
D3=x3 v x5;
D4= x3 v ¬x5;
D5= ¬x3 v ¬x4;
D6= x5;
D7= x4.
D 1,2 = ¬x1 v ¬x2;
D1,2;3 = ¬x1 v ¬x2 v x3 v x5;
D1,2,3;4= ¬x1 v ¬x2 v x3;
D1,2,3,4;5= ¬x1 v ¬x2 v ¬x4;
D1,2,3,4,5;6= ¬x1 v ¬x2 v ¬x4 v x5;
D1,2,3,4,5,6;7= ¬x1 v ¬x2 v x5.
