
СРРиТ / ОПССТ
.docxВариант №21.
Задание 1.
Вопрос №22. Шумы ограничения. Неравномерное квантование. Кодирование квантованных сигналов.
При
квантовании по уровню непрерывный
диапазон амплитуд отсчетов АИМ сигнала
заменяется счетным множеством разрешенных
уровней квантования
 .
При этом непрерывный динамический
диапазон отсчетов АИМ сигнала разбивается
на ряд отдельных участков, называемых
шагами квантования
.
При этом непрерывный динамический
диапазон отсчетов АИМ сигнала разбивается
на ряд отдельных участков, называемых
шагами квантования
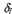 .
Если амплитуда отсчета сигнала
.
Если амплитуда отсчета сигнала
 удовлетворяет условию
удовлетворяет условию
 (1)
(1)
то сигналу присваивается амплитуда, соответствующая i-му уровню квантования.
Таким образом, квантование представляет процесс сравнения отсчета АИМ сигнала со шкалой, имеющей конечное число уровней квантования, и отнесения его к ближайшему разрешенному уровню.
Иными словами, процесс квантования представляет округлению амплитуды отсчета до ближайшего разрешенного уровня.
Последовательность отсчетов и соответствующие им квантованные отсчеты показаны на рис. 1. Устройство, осуществляющее квантование, называется квантующим. Передаточная характеристика квантующего устройства является ступенчатой (см. рис. 1, а), поскольку каждый дискретный выходной уровень соответствует некоторому интервалу значений входного сигнала.
Разность
между сигналом АИМ-2 (см. рис. 1, б) и его
квантованным приближением - квантованным
АИМ сигналом (см. рис. 1, а) называется
ошибкой, или шумом квантования
 ,
величина которого не превышает половины
шага квантования
,
величина которого не превышает половины
шага квантования
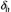 т.е.
т.е.
 (2)
(2)
Из рис. 1, а очевидно, что чем больше разрешенных уровней квантования М, т.е. чем меньше шаг квантования, тем меньше величина ошибки, или шума квантования.
Амплитудная
характеристика квантующего устройства
Uвых
=
 (Uвх),
как следует из рис. 1, а, представляет
собой ступенчатую кривую, имеющую два
характерных участка: зону квантования,
при -U0
(Uвх),
как следует из рис. 1, а, представляет
собой ступенчатую кривую, имеющую два
характерных участка: зону квантования,
при -U0
 Uвx
Uвx
 +U0,
и зону ограничения при Uвх
> U0.
Соответственно, различают шумы квантования
и шумы ограничения.
+U0,
и зону ограничения при Uвх
> U0.
Соответственно, различают шумы квантования
и шумы ограничения.
Если во всем диапазоне значений входного сигнала от -U0 до +U0 величина шага квантования остается величиной постоянной, то такое квантование называется равномерным; если же величина шага квантования изменяется с изменением значения Uвx сигнала, то такое квантование называется неравномерным.

Рис. 1. Процесс квантования. Шумы квантования.
При неравномерном квантовании шаг квантования не остается постоянным, а является переменным и изменяется по определенному закону. Если потребовать постоянства защищенности от шумов квантования в заданном динамическом диапазоне для всех уровней входных сигналов, то можно легко определить, воспользовавшись формулами (3) и (4), зависимость шага квантования от мгновенного значения напряжения Uвх (или тока) квантуемого сигнала:
 (3)
(3)
 (4)
(4)
 (5)
(5)
Из формулы (5) следует, что для слабых сигналов шаг квантования должен быть минимальным и возрастает с увеличением напряжения (тока) сигнала, т.е. должна быть нелинейная шкала квантования. Амплитудная характеристика соответствующего квантующего устройства при неравномерном квантовании показана на рис. 2.

Рис. 2. Неравномерная шкала квантования.
Получение переменного шага квантования может быть реализовано следующими способами:
1) сжатием динамического диапазона сигнала с помощью компрессора (К) перед кодированием его в кодирующем устройстве с линейной шкалой квантования и последующим его расширением экспандером (Э) после декодирования (рис. 3); совокупность операций, проводимых компрессором и экспандером, называется компандированием сигнала; характеристика компандирования (К - Э), т.е. каскадного соединения компрессора и экспандера, должна быть линейной;
2) нелинейным кодированием и декодированием;
3) цифровым компандированием.
Для
зависимости, изображенной на рис. 3, где
по осям отложены нормированные значения
входных х = Uвx/Uвxмaкс
и выходных у = Uвых/Uвыхмакс
сигналов, добиваются того, чтобы при
изменении
 приращение
приращение
 было бы постоянным, а приращение
было бы постоянным, а приращение
 - обратно пропорционально наклону
характеристики, т.е.
- обратно пропорционально наклону
характеристики, т.е.
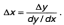 (6)
(6)

Рис. 3. Реализация неравномерной шкалы квантования с помощью компандерных устройств.
Соответственно шаг квантования по оси х будет равен
 (7)
(7)
Если число уровней квантования М в нормированном (от 1 до минус 1) диапазоне, то
 (8)
(8)
Среднюю
мощность шума, обусловленного неравномерным
квантованием, если вместо шага квантования
 подставить его значение в каждом шаге
квантования.
подставить его значение в каждом шаге
квантования.
 (9)
(9)
Для расчета мощности шумов квантования при большом числе уровней квантования М операцию суммирования можно заменить интегрированием, тогда
 (10)
(10)
здесь W (x) - плотность распределения вероятности нормированного сигнала на входе квантующего устройства.
Мощность сигнала можно выразить через его плотность распределения вероятности W (х) нормированного сигнала на выходе квантующего устройства

Тогда отношение сигнал-шум квантования (ОСШК) с учетом (10) будет иметь вид
 (11)
(11)
Для обеспечения постоянства ОСШК необходимо, чтобы
 (12)
(12)
Подставив в формулу (12) выражение (6), получим

Так
как
 постоянно, то получим
постоянно, то получим
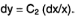
Проинтегрировав правую и левую части последнего выражения, получим

где
 - постоянная интегрирования. Отсюда
- постоянная интегрирования. Отсюда
 (13)
(13)
Для
нахождения постоянных этого выражения
необходимо учитывать граничные условия
закона изменений
 1) при х = О, у = 0 и 2) при х = 1, у = 1.
1) при х = О, у = 0 и 2) при х = 1, у = 1.
Первое условие приводит к нереализуемому результату.
Зависимость полученной функции не переходит через начало координат (рис. 4). Чтобы обеспечить реализацию, следует несколько изменить выражение (13) или изменить начальные условия.
При изменении выражения (13) под знак логарифма вводим постоянную С3:
 (14)
(14)
тогда,
подставляя нулевые граничные условия,
получим значение постоянной С3
= 7. Подставив второе граничное условие,
найдем значение для С2


Рис.
4. Характеристики
 закона
компандирования.
закона
компандирования.
Подставив последнее выражение в (14) и учитывая, что С3 = 1, получим,
 (15)
(15)
Кодирование квантованных сигналов Квантованный сигнал, в принципе, можно считать кодовым с основанием кода, равным числу М разрешенных уровней (уровней квантования), и с числом символов в кодовой группе, равным единице. Таким образом, квантованный сигнал является многоуровневым.
Многоуровневые сигналы весьма неудобны для передачи, так как приемник должен различать все разрешенные уровни. Кроме того, такие сигналы трудно восстановить (регенерировать), если они подверглись действию помех. Иными словами, многоуровневым сигналам в большей степени свойственны недостатки аналоговых сигналов. Поэтому в цифровых системах передачи обычно используются коды со сравнительно низким основанием, чаще всего двоичные. Процесс преобразования многоуровневого сигнала в код с низким основанием называется кодированием. Результатом кодирования является комбинация символов (посылок, цифр), представляющая в соответствующей системе счисления номер разрешенного уровня квантованного сигнала. В цифровых системах передачи широкое применение нашла двоичная система счисления.
Запись любого квантованного уровня с М разрешенными уровнями в двоичной системе счисления может быть представлена в виде
 (16)
(16)
здесь т - число разрядов кода; аi - разрядная цифра, принимающая значения 0 или 1. С помощью m-разрядного двоичного кода можно закодировать число уровней квантования, равного
М = 2m. (17)
Поскольку выбор числа уровней квантования определяется допустимой величиной шага квантования, обычно приходится решать обратную задачу: определение минимально необходимого числа разрядов кода, который может быть использован для кодирования при заданном М. Из (17) очевидно, что для двоичного кода имеем
 (18)
(18)
здесь ent (х) - означает, что берется целая часть числа х.
Например, для кодирования числа 111 необходимое число разрядов будет равно m = ent (1og2 М) = ent (log2111,)= ent (6,79) = 7, а запись числа 111 будет иметь вид

т.е. ему соответствует кодовая комбинация 1101111, что соответствует значениям разрядных цифр равных а6 = 1, а5 = 1, а4 = 0, а3 = а2 = а у = а0 = 1. Набор величин Qm-1 = 2m-i можно рассматривать как ряд эталонных сигналов, имеющих вес, определенный номером разряда.
Для нашего примера Q6 = 64, Q5 = 32, Q4 = 16, Q3 = 8, Q2= 4, Q1 = 2, Qo=1.
Однозначная связь величины эталонного сигнала с номером разряда двоичного эквивалента разрешенного квантованного уровня позволяет ограничиться передачей в системе связи только ряда величин аi, составляющих кодовую комбинацию (или кодовую группу).
Множество используемых кодовых комбинаций, связанных единым законом построения, называется кодом. Простейшим кодом является код, в основе построения комбинаций которого лежит отношение (16), называется натуральным двоичным кодом.
Графически коды удобно изображать кодовыми таблицами, или кодовыми растрами, характеризующими форму взаимной связи уровней квантования и соответствующих им кодовых комбинаций, представляя их по порядку уровней. На рис. 5, а показан кодовый растр пятиразрядного натурального двоичного кода, с помощью которого можно образовать 32 двоичных числа - кодовые комбинации и, следовательно, передать 32 квантованных уровня; 1 («единицы» или «импульсы») и 0 («нули»или «пробелы») показаны здесь соответственно черными и белыми квадратиками. Нумерация уровней дана сверху вниз, вверху указан вес разрядов кода.
Перестановка порядка следования кодовых комбинаций на обратный дает простой обратный код. Например, уровень М = 22 в натуральном коде представляется комбинацией вида 10110 (см. рис. 5, а), обратный код выразится комбинацией вида 01101.
Замена всех импульсов в кодовой комбинации на пробелы (или «единиц» на «нули») приводит к инверсному коду. Так, для М = 22 в натуральном коде кодовая комбинация в инверсном коде будет иметь вид 01001.
Другой тип кода, применяемый в цифровых системах передачи, - код Гоея (он же рефлексный или зеркальный). Его отличительной особенностью является то, что любые две соседние кодовые группы (см. рис. 5, б) отличаются друг от друга лишь в одном разряде.
Это свойство используется при построении кодов и позволяет уменьшить ошибки кодирования. К коду Грея применимы понятия обратный или инверсный.
Еще один класс составляют симметричные коды. Для кодирования отсчетов, например, речевых - телефонных сигналов, которые принимают более или менее одинаковые абсолютные значения выше и ниже своего нулевого уровня, может оказаться удобным использовать первый разряд для обозначения знака полярности, т.е. положительного или отрицательного, а остальные разряды обозначения абсолютной величины. Если не принимать во внимание первый (высший) разряд, определяющий полярность квантованного АИМ сигнала, то получающаяся кодовая таблица (кодовый растр) оказывается симметричной относительно своей середины. Ясно (см. рис. 5, б), что код Грея также обладает свойством симметрии.

Рис. 5. Кодовые таблицы двоичных кодов: а - натуральный двоичный код; б - рефлексный двоичный код Грея; в - симметричный двоичный код
Перечисленными кодами техника цифровых систем передачи не ограничивается. Предложено большое количество кодов, целесообразность использования которых решается конкретными задачами кодирования и требованиями к достоверности передаваемой цифровой информации.
Кодовые группы после передачи по линейному тракту декодируются на приеме, и по отсчетным значениям восстанавливается исходный сигнал.
В современных ЦСП процессы квантования и кодирования, как правило, совмещены и процесс формирования цифрового сигнала называется аналого-цифровым преобразованием (АЦП), а обратный процесс называется цифро-аналоговым преобразованием (ЦАП). Кодеры и декодеры, предназначенные для АЦП и ЦАП, в совокупности называются кодеками.
Задача 2.
Рассчитать шумы квантования и ограничения телефонного канала и определить результирующее отношение сигнал/шум.
 дБ
дБ


Решение:
Шумы квантования при равномерном квантовании определяются выражением:

 – пик-фактор
сигнала;
– пик-фактор
сигнала;
 – среднеквадратичное
отклонение полезного сигнала;
– среднеквадратичное
отклонение полезного сигнала;
 – разрядность
кодирования.
– разрядность
кодирования.

Шумы ограничения
определяются выражением:


Результирующее значение отношения сигнал/шум:


Задача 3.
Рассчитать защищенность от переходной помехи первого и второго рода в системе с временным разделением каналов и амплитудно-импульсной модуляцией.
 кГц
кГц
 кГц
кГц
 кГц
кГц
 мкс
мкс
 кГц
кГц
Решение:
Защищенность от переходной помехи 1-го рода:

 – длительность
защитного интервала;
– длительность
защитного интервала;
 – верхняя граничная
частота канала.
– верхняя граничная
частота канала.

 – длительность
импульсов.
– длительность
импульсов.

 дБ
дБ
Защищенность от переходной помехи 2-го рода:

 дБ
дБ
Задача 4.
Динамический
диапазон сигналов в линии связи
определяется в децибелах и равен
 .
Его значение принимается равным
порядковому номеру зачетной книжки,
превышающему 10. К цифрам до 10 следует
прибавить 10. Определить вероятность
обнаружения сигнала при пороговом
отношении сигнал/шум равном единице и
отношении сигнал/шум равном максимальному
значению. Считать плотность распределения
вероятностей значений принимаемого
сигнала гауссовской, мощность шума
10-12
Вт.
.
Его значение принимается равным
порядковому номеру зачетной книжки,
превышающему 10. К цифрам до 10 следует
прибавить 10. Определить вероятность
обнаружения сигнала при пороговом
отношении сигнал/шум равном единице и
отношении сигнал/шум равном максимальному
значению. Считать плотность распределения
вероятностей значений принимаемого
сигнала гауссовской, мощность шума
10-12
Вт.
 дБ
дБ
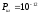 Вт
Вт
Решение:
Динамический диапазон сигналов в линии связи определяется как
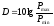

Вероятность обнаружения сигнала при пороговом отношении сигнал/шум равном единице и отношении сигнал/шум равном максимальному значению

Задача 5.
Определить вероятность ошибки обнаружения сигнала в канале связи при пороговом отношении сигнал/шум равном порядковому номеру зачетной книжки. Чувствительность приемника определить для шумовой температуры 293° К и полосе пропускания численно равной порядковому номеру зачетной книжки в мегагерцах. Считать входное сопротивление приемника согласованным с коаксиальным кабелем антенно-фидерного устройства 50 Ом.

 МГц
МГц
 К
К
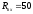 Ом
Ом
Решение:
Чувствительность приемника для шумовой температуры 293° К и полосы пропускания 21 МГц:
 .
.
На вход приемника поступает сигнал мощность 0,41 мВ
Отношение сигнал/шум:

Вероятность обнаружения сигнала будет равна

Литература
1. Основы построения телекоммуникационных систем и сетей: Учебник для вузов / В. В. Крухмалев, В. Н. Гордиенко, А. Д. Моченов и др.; Под ред. В. Н. Гордиенко и В. В. Крухмалева. - М.: Горячая линия - Телеком, 2004.
2. Тепляков, И. М. Основы построения телекоммуникационных систем и сетей / И. М. Тепляков. – М. : Радио и связь, 2004.
3. Крук, Б. И. Телекоммуникационные системы и сети. Т. 1 : Современные технологии : учеб. пособие для высших учеб. заведений / Б. И. Крук, В. Н. Попантонопуло, В. П. Шувалов. – М. : Горячая Линия – Телеком, 2003.
4. Ломовицкий, В. В. Основы построения систем и сетей передачи информации / В. В. Ломовицкий. – М. : Горячая Линия – Телеком, 2005.
